Whether standing in the shower, spilling the morning coffee or going to work in the rain, each day typically begins with water droplets splashing off a solid surface. In fact these phenomena are so common that they often go unnoticed. However, the basic physics that governs the dynamics of water droplets is extremely rich, and understanding these events in detail has important scientific and technological consequences.

In agriculture, for instance, the wax-like outer layer of a plant leaf produces a non-wetting interface that repels water and causes drops to bounce off the surface. As a result, the plant often retains less than half of an applied spray. This is both inefficient and hazardous, since the herbicides and pesticides that are destined for the plant can build up and eventually contaminate the soil and public water supplies. Finding a way to eliminate droplet rebound in such cases has both major economic and social benefits.

On the other hand, promoting droplet rebound so that all drops bounce off a surface can have many advantages. Imagine a car windscreen that can repel every raindrop in a downpour. It would make driving in the rain much safer. Perhaps we can learn from the natural ability of plants to repel droplets and apply the same strategy to car windows. Thus, one sees that preventing or enhancing drop rebound off a surface can have a significant impact on our daily lives.

Making contact

The hydrodynamics of droplet impact is fascinating. In the late 19th century A M Worthington carried out pioneering work on the forms assumed by drops of liquids as they fall vertically onto a horizontal plate. These observations revealed the many different phenomena that can occur during rebound.

Like many seemingly simple physical phenomena, the process of a drop hitting a surface is much more complicated than it first appears. Aspects of the drop – its size, speed and the nature of the fluid – have to be considered, as have the chemical composition and physical structure of the surface. Indeed, the same drop that bounces off a leaf will stick to the sides of a bathtub. In addition, the events that take place at impact last only a few milliseconds, making detailed observations of the drop complicated.

In 1957 this problem prompted Harold Edgerton at the Massachusetts Institute of Technology to apply his now-famous stroboscopic photography techniques to capture images of drops plunging into a bowl of milk. Today modern instruments allow us to directly observe these rapid events rather more easily. High-speed cameras typically record 10³ to 10⁴ frames per second and can save images in formats that standard household video recorders can read. This is where our work has its origins.

When a drop encounters a solid surface, its initial spherical shape is forced into a pancake-like form that stretches out over the surface. The kinetic energy of the drop forces it to conform to the planar geometry of the solid surface. If the liquid in the drop is attracted to the surface, it will continue to spread and eventually adhere to the so-called hydrophilic material. The extent of the spreading is determined by the molecular interactions between the fluid and the solid.

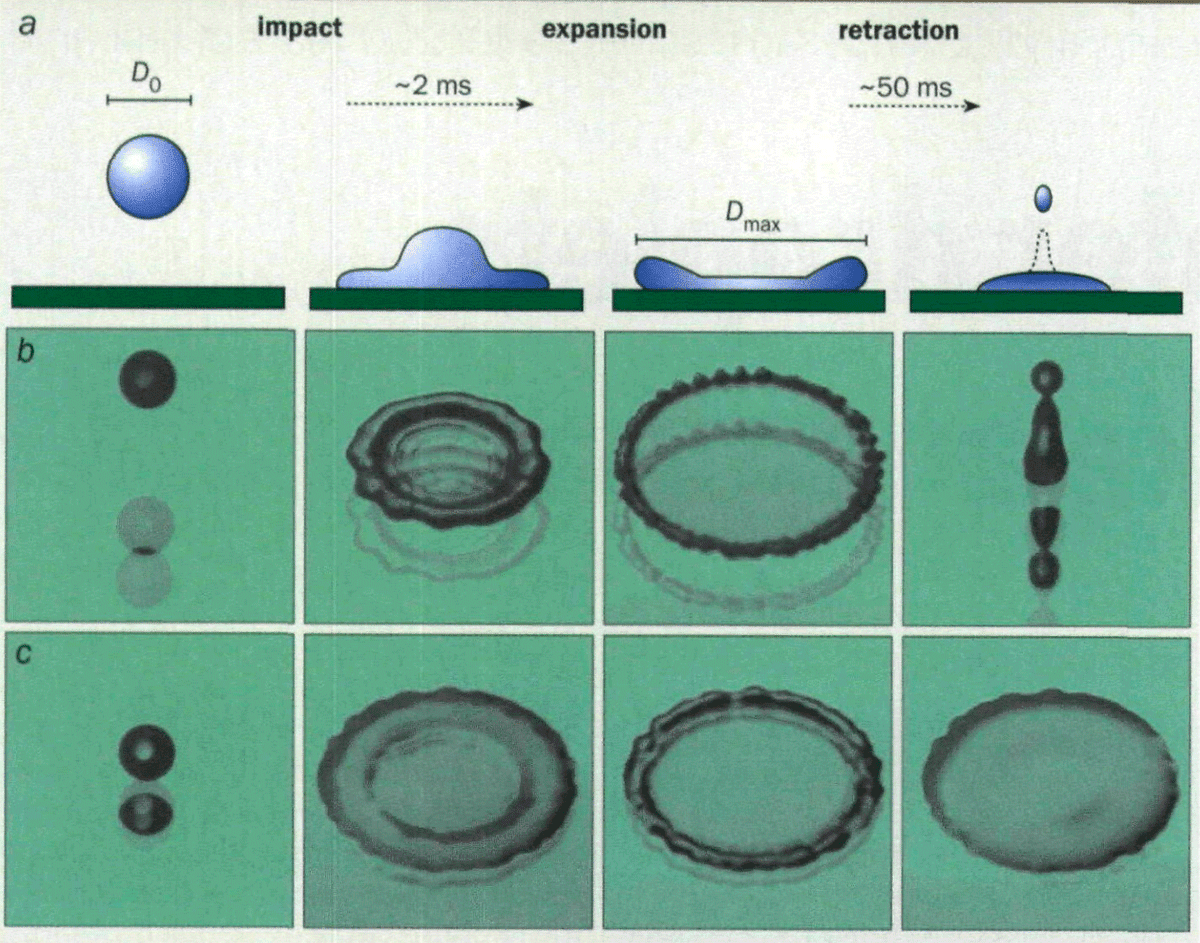
When the molecular interactions between the water and the surface are repulsive, water droplets landing on these so-called hydrophobic solids try to minimize their contact with the surface. Thus, after being forced into a pancake shape, the drops retract as they try to re-establish a spherical form to minimize their exposure to the solid. Indeed, for certain cases the retraction can be sufficiently violent that the drop actually rebounds or bounces off the surface after impact (figure 1b).

Scratching the surface

Many plant surfaces are capable of promoting droplet rebound quite efficiently, but what makes their surfaces so good at doing this? A close look at the surface of a lotus leaf provides a clue as to why many natural materials are extremely hydrophobic in character (figure 2). First, the surface of these leaves is usually covered with a range of different waxes made from a mixture of large hydrocarbon molecules that have a strong phobia of being wet. Second, microscope observations reveal that the surface is made of bumps that are about 10 µm wide and these, in turn, are covered with hollow tubes that are roughly 1 µm in diameter.

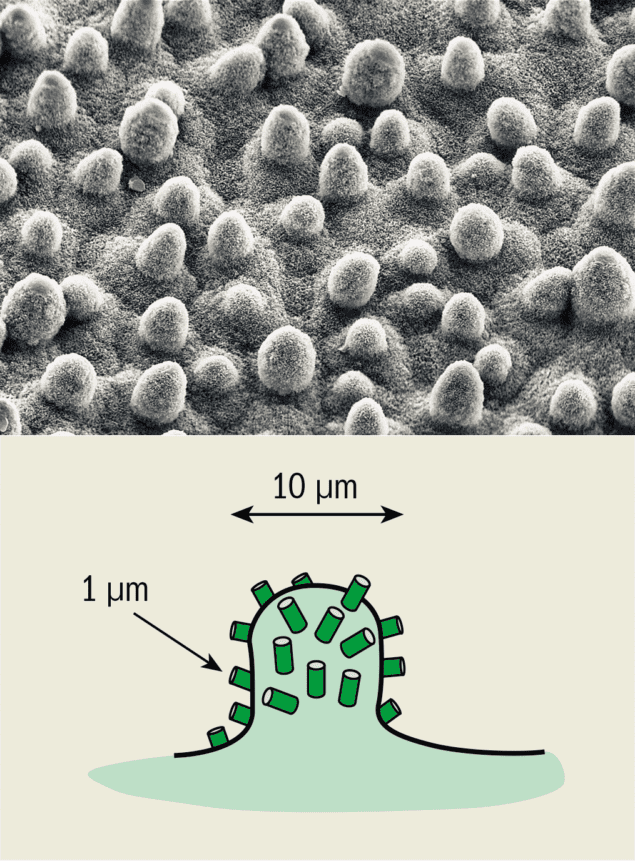
Water cannot enter the cavities created by these bumps because the surface is hydrophobic, so the drop is left stranded on a pincushion of spikes. The gap between these spikes means that the drop is mostly in contact with the air, with only a very small part of it actually touching the leaf. This combination of repulsive chemical interactions and the physical morphology of the leaf creates a surface that is capable of efficiently repelling water and generating astonishing hydrophobic behaviour.

Other examples of this non-wetting approach can be found in duck feathers and butterfly wings. These corrugated surfaces also provide air pockets that prevent water from completely touching the surface. As a result of the limited contact that the drops have with the surface, there is very little friction against drop motion. This means that water can bounce or roll off duck feathers and butterfly wings quite easily.

Artificial surfaces can be constructed to mimic this behaviour by chemically treating them with water-repellent substances like silicone and Teflon, or by fabricating extremely rough hydrophobic surfaces directly. For example, Tomohiro Onda and colleagues at Kao Corporation in Japan have recently developed ultra-rough hydrophobic surfaces by coating glass plates with a molten wax that undergoes fractal growth as it solidifies. Alternatively, pre-designed patterns can be etched onto a smooth surface to provide precise control over the morphology, this can then be treated with hydrophobic chemicals. The practical applications of such techniques cover an enormous range, from waterproof clothes and paint to car windscreens.

By adapting these strategies, our groups at the Ecole Normale Supérieure and the Collège de France in Paris have made surfaces that have quite startling hydrophobic properties. So much so that water drops bounce like basketballs when they are dropped onto the surface (figure 3). Indeed, we have observed drops rebounding over 20 times before they eventually roll along the surface. We have also found that the elasticity of the water drops is very high – the ratio of their velocity before and after the impact, the so-called restitution coefficient, is as high as 0.9 throughout the trajectory. This elasticity arises from the efficient transfer between kinetic and surface energy during drop deformation.

However, we also see clear signs of damping with each successive bounce. The origin of this damping is in the vigorous vibrations of the drop after it lifts off the surface. As the translational kinetic energy is transferred into vibration modes, viscous dissipation occurs between each impact due to the motion of the fluid in the drop. A close look at the photograph in figure 3 shows ripples in the lines of light that trace the drop’s flight, which clearly reveal the effect.

Rebounding water droplets are somewhat similar to the problem of bouncing solid spheres that was first analysed in detail by the German physicist Heinrich Hertz in the early 1880s. Like Hertz, we also measured the time of contact between the drop and the surface. For millimetre-sized raindrops, this time is of the order of 3 milliseconds. Our quantitative examination reveals that a free-falling drop vibrates on the same timescale. In other words, the drop vibrates like a forced oscillator and the time with which it is in contact with the surface sets the oscillation period. Once set in motion, the in-flight behaviour of the drop follows the dynamics that were derived in the late 19th century by Lord Rayleigh and discussed more recently by Subrahmanyan Chandrasekhar.

Making water stick

So we seem to be able to copy nature’s ability to make non-wetting surfaces, but can we cope with the problems these surfaces pose when we want to treat them? For many years extensive research efforts have focused on viable ways to prevent water drops from bouncing off hydrophobic surfaces. The challenge is to add something to the water that will short-circuit the mechanisms that drive droplet rebound, without significantly altering the intrinsic properties of the water. This requires a closer look at the moment of impact (figure 4a).

In the first few milliseconds after it has hit the surface, the drop is forced to spread rapidly to a maximum diameter. A rebounding drop then retracts quickly until it eventually leaves the surface. How can we make the drops retract slowly and stay fixed to the surface? Understanding the forces involved during drop impact leads to the possibility of controlling these events.

The physical parameters that determine if the drop will stick to the surface or rebound are the inertial, viscous and capillary forces that act as the drop impacts and begins to expand. The inertial forces result from the kinetic energy of the drop, and are determined by the drop’s size, density and speed. Meanwhile, the fluid viscosity of the drop governs the viscous dissipation, and the capillary force (i.e. surface tension) establishes the energy that is required to deform the drop. These parameters are typically used to define two dimensionless numbers that gauge the relative strength of the forces that oppose one another. The Reynolds number, Re, is a ratio of the inertial and viscous forces, while the Weber number, We, is the ratio of the inertial and capillary forces. In other words, the inertial forces are in competition with the viscous dissipation and the drop deformation.

Intuition tells us that slow-moving, highly viscous drops – which have low Reynolds and Weber numbers – can dissipate all of their kinetic energy on impact, leaving nothing to propel them off the surface. We clearly don’t expect, for example, a drop of honey to rebound from a surface because it is so viscous. But high viscosity has its drawbacks – which explains why liquids like honey never come in squirt bottles or pressurized spray cans. All spray-coating techniques require us to pump and atomize the fluid, and this can not be done if the liquid is too viscous. Thus trying to prevent rebound by simply increasing the viscosity isn’t a useful solution.

Lowering the tension

In nearly every practical circumstance that requires us to control droplet rebound, we are forced to deal with fast-moving, low-viscosity fluids. In other words, we must consider the impact and expansion of droplets that are driven by inertial forces and that have large Reynolds and Weber numbers. The drops have a high kinetic energy as they hit the surface, which is not dissipated as the drops expand. This means that similar-sized drops spread to the same maximum diameter. Faced with this situation, we must turn our attention to the final retraction stage of the process.

When a drop expands to its maximum diameter, most of its kinetic energy is transferred into deforming it into a pancake shape. Once this has happened, the situation changes and the drop begins to recoil. The forces driving this action are the desire of the drop to reform to a sphere, and the drop struggles against the motion of the fluid to do so. This competition can be described by a dimensionless quantity known as the capillary number, Ca, a ratio of the capillary and viscous forces. This quantity can also be expressed simply as Ca = We/Re, the ratio of Weber and Reynolds numbers.

A convenient way to think about the recoiling drop is to draw an analogy with a spring and “dash pot” – a device that can be used to damp vibrations. Imagine pulling a cylinder that is connected to a spring through a cup of fluid until the maximum spring extension is reached. When the cylinder is released, strong springs tend to pull it out of the cup while a viscous fluid can prevent this from happening. Similarly, high surface-tension forces can propel a drop from the surface, while dissipation within the fluid can hold it back by using up all of its stored energy. This suggests two ways to keep the retracting drop on the surface: we can either decrease the surface tension or increase the fluid viscosity. We need to remember that high viscosities cause problems for pumping and spraying, but there are still a few tricks that we can use.

Decreasing the surface tension of water is easy using molecules called surfactants. One part of a surfactant molecule is attracted to water while another part is repelled. As a result, surfactants readily position themselves at the air-water interface and can significantly lower the surface tension, by over a factor of two in some cases. This sounds promising, but one issue that makes using this idea difficult is the time that it takes for the surfactant molecules to reach to the surface. If they fail to arrive at the interface in the time it takes the drop to expand, then they have no effect on the recoil.

Two teams on opposite sides of the Atlantic – one led by Osman Basaran of Purdue University in the US, the other by Michèle Vignes-Adler at Université de Marne-la-Vallée – realized this problem. Using high-speed photographs, each group independently showed that drop rebound can be controlled if the surfactants can lower the tension quickly enough. Basaran and Vignes-Adler call this property the “dynamic surface tension” of the system. By measuring the dynamic surface tension and systematically comparing different types of surfactants, both teams found a clear correlation between the fast lowering of the tension and bounce-resistant drops.

Rapid lowering of the tension is one way to help control droplet rebound. However, it is not particularly well suited to spray applications because the same tension-lowering effect creates smaller droplets that can easily drift off target. Drop rebound isn’t an issue if none of them land on the surface! This sent us looking for an alternative.

Going with the flow

In 1997 Louis Vovelle at Rhodia, the specialist chemical company in Lyon, France, began to reconsider the effect of viscous dissipation. As he was mixing some dilute polymer solution, he noticed something very interesting dangling from his shirt sleeve. A drop of the polymer solution had formed a long filament before it eventually dripped off. This filament held the key. Vovelle understood that this ability of the fluid to stretch before falling to the ground could be influenced greatly by certain nonlinear viscosity effects. In particular, dilute aqueous polymer solutions can have extremely high “elongational viscosities”. This viscosity describes a fluid’s resistance to deformation – unlike the standard “shear viscosity”, which accounts for the molecules rubbing against one another.

Interestingly, the same polymer solutions have a very low shear viscosity, equal to that of pure water. Moreover, Jun Fukai of Kyushu University in Japan and Dimos Poulikakos at the Swiss Federal Institute of Technology in Lausanne have considered the detailed hydrodynamics of a drop hitting the surface using numerical simulations. Their results show that the fluid in the drop undergoes extreme deformations as soon as it hits the surface.

Putting this together, Vovelle came to the conclusion that a dilute polymer solution should be perfect for preventing droplet rebound. The high elongational viscosity should dissipate the kinetic energy of the drop during the strong deformational flow, without increasing the shear viscosity that causes pumping problems. The idea was tested and shown to work with dilute solutions containing as little as 0.1 gramme of polyethyleneoxide (PEO) per litre of water (figure 1b). The polymer is scattered throughout the solution in small discrete clumps that have no noticeable effect on the solution’s properties. However, the stretching action that occurs during the drop expansion and retraction unfolds and deforms the polymer. This deformation drains enough energy out of the drop so that it can no longer escape the surface (figure 5).

At about the same time, David Boger and Regan Crooks of the University of Melbourne in Australia demonstrated the identical effect and studied a wide range of fluids and conditions. And Jeff Cheny and Ken Walters at the University of Wales at Aberystwyth showed that these dilute polymer solutions can also have a profound effect on drops splashing into a solution. They found that the elongational viscosity can dramatically reduce the height of the so-called Worthington jet – the jet of fluid that rises from a solution when a drop breaks the surface.

Furthermore, solutions that possess a high elongational viscosity tend to create larger drops when sprayed, rather than smaller ones. The reason is that the elongational viscosity stabilizes the neck of fluid as it leaves the nozzle, preventing the formation of small satellite drops. This is a big advantage for agricultural-spray applications because larger drops are less susceptible to drift in the wind so the farmer has a better chance of getting the product where it is needed.

Practical applications

So can these ideas of nonlinear viscosity really be applied to real-life applications? Faced with this challenge, Rhodia’s research teams – led by one of us (VB), Vovelle and Jean-Yves Martin – developed an anti-rebound, drift-control additive that could be used in a broad range of agricultural sprays. The model system of a dilute PEO solution provided the proof-of-concept that we needed, but several obstacles stood in the way.

First, the additive must not react with other chemicals in the spray. Unfortunately, PEO is notorious for interacting with many of the components that are commonly used in agricultural herbicides and insecticides. These chemical reactions interfere with both the polymer’s performance and the function of the active components in the formula.

Second, PEO is a synthetic product, and to be effective one needs to use extremely large molecules with molecular weights of 5000 kg per mole. (By comparison the molecular weight of water is only 18 g per mole.) This makes it difficult to make the polymer molecules more soluble. And it also makes it difficult for the molecules to biodegrade once they have been sprayed. PEO isn’t necessarily the best polymer available. However, other synthetic polymers that have a high elongational viscosity, such as polyacrylamide, suffer from the same problems and also tend to degrade under shear during pumping. Addressing these issues required bringing together the physicists, chemists, toxicologists, technologists and business units in the company.

The result of this effort has produced a series of products based on naturally occurring polymers known as polysaccharides. These polymers are essentially giant sugar molecules that are found in abundance throughout nature. Armed with the knowledge that it is the elongational viscosity that counts, and shuffling through the many varieties of water-soluble polysaccharides that exist, the search was narrowed down to a class of polysaccharides known as guar gum. This polymer is extracted from the Cyamopsis tetragonoloba taub plant found in India and Pakistan, and is used widely as a food additive. This makes it excellent for spraying onto plants. In addition, the anti-rebound properties of a slightly modified version of this polysaccharide are far superior to that of PEO and other synthetic products.

Rhodia now successfully markets these products as aids for a wide range of spray products. The market for these products is quite large: the global market for generic herbicides is worth over $1 billion dollars. Add to this the insecticide and fungicide markets, and it is easy to see why Rhodia has developed a sweet taste for these giant sugar molecules from India.

Looking to the future, there is a host of potential uses for this anti-rebound technology on the horizon, in water-based household cleaners and paints in particular. These products are found in squirt bottles and pressurized spray cans on almost every supermarket shelf. They can be made far more efficient for cleaning and coating plastic surfaces by adding an anti-rebound polymer. Similarly, personal-care products, such as hairsprays and deodorants, can also benefit from enhanced droplet deposition.

But perhaps one of the biggest potential uses will be for ink-jet printing. The high impact velocity of the ink makes accurate droplet formation and printing a significant challenge. The development of new ink formulations that have a specific elongational viscosity will give much greater control over the printing process. Indeed, the same polymeric solutions that Rhodia developed for the agricultural-spray droplets should be well suited for up and coming water-based inks. Droplets that don’t rebound are destined to make a big splash.