Gravitational waves offer a unique way of studying inflation and other fundamental processes of the very early universe, explains Craig J Hogan, and may even connect string theory with the world of experiment

Our view of the universe is about to change forever. Since science began, all our knowledge of what lies above, below and around us has come from long-familiar forms of energy: light, produced by distant astrophysical objects; and matter, in the form of particles such as cosmic rays. But we are now in a position to study the universe using an entirely different form of energy that until now has never been directly detected – gravitational waves.
A key prediction of Einstein’s general theory of relativity, gravitational waves are vibrations of space–time generated by the acceleration of all forms of mass and energy. Extreme gravitational environments such as black holes or neutron-star binaries generate waves with the largest amplitudes, while the frequency of the waves depends on how such sources move. Small-scale motions, such as those of stellar-mass black holes, generate high-frequency gravitational waves, while larger objects, such as massive black holes, move more slowly and produce lower-frequency signals. Passing through material of any kind at the speed of light, gravitational waves fill the entire universe and may therefore carry information from the beginning of space–time itself.
Around the world several gravitational-wave detectors are currently taking data, in the hope that they will detect these tiny disturbances of space–time directly for the first time. These large interferometers – LIGO in the US, GEO-600 in Germany, VIRGO in Italy and TAMA in Japan – are all looking for minute changes in the relative lengths of two kilometre-scale arms induced by a passing gravitational wave. In the next few years they should be able to detect the high-frequency signals (roughly 100 Hz or more) produced by the most extreme gravitational objects (see figure 1).
Gravitational-wave detectors are not restricted to the Earth: an international project called the Laser Interferometer Space Antenna (LISA) is currently awaiting critical funding decisions that could see it launched in about 2017. Away from the noisy environment of our planet, LISA’s three spacecraft will use lasers to form a trio of interferometer arms each five million kilometres long. The mission will therefore be able to detect disturbances in space–time down to 1 mHz and below, probing a region of the gravitational-wave spectrum that is known to contain a large number and variety of sources.
Since gravitational waves allow us to study the universe with a new form of energy that couples to everything, gravitational-wave detectors may also lead to totally unexpected discoveries – as did the telescope and the microscope in their times. Moreover, gravitational waves provide a detailed record of events that took place in the first second or so of the universe, which should allow us to constrain models such as cosmic inflation and other extreme and uncharted physics of the early universe. Indeed, these ghostly disturbances of space–time effectively turn the early universe into a sophisticated laboratory for ultrahigh-energy physics that could help tackle the problem of quantum gravity.
Probing inflation
Gravity has already revealed to us an invisible universe. About 70 years ago, Fritz Zwicky discovered the gravitational effects of what we now call dark matter, when he realized that the speed with which certain galaxies move could not be explained by the amount of visible matter. Determining the nature of dark matter alone – which is now thought to make up about 21% of the universe – is one of the great challenges of modern physics. Furthermore, about 10 years ago astronomers found that an even larger fraction of the universe (about 75%) is made up of “dark energy” – a gravitationally repulsive substance that is causing the expansion of the universe to accelerate. Can we even begin to guess what we might find when we use gravity itself to probe the universe?
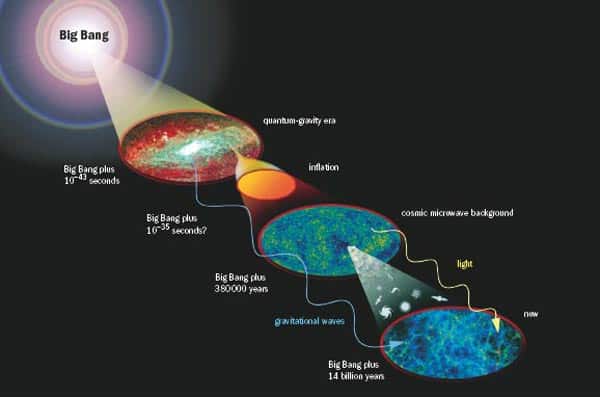
While we are likely to discover unforeseen sources of gravitational waves in the recent (i.e. nearby) universe, one great hope is that gravitational-wave detectors will tell us about the extreme gravitational conditions that existed much earlier in the universe’s history (see figure 2). Electromagnetic radiation has already provided direct evidence of many processes that took place in this era. For example, the spectra from distant matter has indirectly shed light on how light nuclei were produced in the first few minutes of the universe, while the cosmic microwave background provides a snapshot of the universe as it was 380 000 years after the Big Bang.
This background – a cold sea of low-frequency electromagnetic radiation – was produced after the universe had expanded and cooled sufficiently to allow hydrogen atoms to form (a process called recombination). Photons that had previously been scattered by charged particles in the primordial plasma could now propagate freely – their observed wavelength today having been stretched to the microwave region. The cosmic microwave background has told us much about the propagation of acoustic waves in the primordial plasma, among other important results such as the geometry of space (see “The cosmic microwave background”). But gravitational waves can tell us much more about the early universe by probing motion that occurred at such early times and on such small scales that its electromagnetic traces have long since been washed out in thermal equilibrium (see figure 2).
The idea that currently generates the most excitement is the possibility of detecting gravitational waves from cosmic inflation, a period of accelerated expansion that began immediately after the Big Bang during which the volume of the universe increased by a factor of up to 1080 in a tiny fraction of a second. Inflation is the best model we have for explaining the large-scale structure of the universe – in other words, for making the universe big, for kick-starting cosmic expansion and for producing the fluctuations in space–time that seeded galaxy formation. Yet we know very little about the physics of this extremely brief chapter of cosmic history.
As gravitational waves were produced by motion on the quantum scale during inflation, detecting them would indicate the existence of gravitons – the hypothetical particles of gravity and hence space–time itself. These single quanta are thought to have imprinted small fluctuations onto the fabric of space–time that were blown up to enormous scales by inflation. Detecting such primordial gravitational waves would therefore test whether quantum mechanics is correct under very high densities. It would also allow cosmologists to estimate parameters such as the rate of inflationary expansion, which are currently poorly constrained.
Primordial waves
The best way to search for these early gravitational waves is to study the cosmic microwave background (CMB) radiation. Thanks to many beautiful results from experiments such as the Cosmic Background Explorer (COBE) and the Wilkinson Microwave Anisotropy Probe (WMAP), we have already detected the imprint of other quanta in the CMB – work for which COBE researchers John Mather and George Smoot were awarded the 2006 Nobel Prize for Physics. Small differences in the temperature of the microwave background in different patches of the sky are direct evidence for fluctuations in the “inflaton field” that drove inflation. These fluctuations are the reason why matter clumped together to create the galaxies and other cosmic structure that we see today. With even more heroic experimental efforts it may be possible to tease out the much weaker signature of gravitons in the microwave background.
In order to separate the contributions of the graviton- and inflaton-induced fluctuations, we need to study the polarization of the CMB. These photons became polarized – i.e. the electric-field component of the electromagnetic wave tends to point in a particular direction – when they scattered off free electrons either during recombination or a few hundred million years later when the first stars formed and reionized the surrounding gas. Because the pattern of temperature fluctuations in the CMB has a “quadrupolar” component – that is, it is brighter along some axes than along others – the electrons are made to jiggle more along certain directions. This gives rise to different polarizations, but the quadrupolar signal generated by gravitational waves is special because gravitational waves themselves have a purely quadrupolar character. (It is this property that allows us to detect gravitational waves using interferometers, see figure 3.) As a result, gravitational waves can generate polarization fluctuations even in places where there is no local temperature perturbation.
In 2001 researchers working on the DASI experiment in Antarctica detected polarization fluctuations in the CMB at the level expected – i.e. a few per cent of the temperature fluctuations – and since then other experiments including WMAP, BOOMERANG and the Cosmic Background Imager have verified and extended the DASI results (see figure 4). But disentangling the particular polarization signal expected only from gravitons – which involves a vortex-like pattern of polarization – is much harder because its contribution is so small. Detecting the polarization pattern at fainter levels is the target of new experiments such as the Robinson Gravitational Wave Background Telescope (“BICEP”) in Antarctica and of a variety of planned and proposed experiments both on the ground and in space, including the European Space Agency’s Planck Explorer and, eventually, NASA’s Beyond Einstein Inflation Probe.
Indeed, one day it might even be possible to detect these graviton-induced inflationary gravitational waves directly using an interferometer. Given the weakness and high frequency of the signal, the capability to do this is decades away. But one should always bear in mind the possibility of the unexpected. For example, there are exotic “pre Big Bang” versions of cosmology in which the high-frequency waves are strong enough to even be detected with current technology.
If the graviton pattern is found, it will reveal much about how fast the universe expanded during inflation and indeed about gravity itself, since direct imprints of gravitons provide a convincing test of quantum mechanics under unimaginably remote and extreme conditions. On the other hand, like many of the other gravitational effects described here, it might not be detected at all. If inflation happened too slowly, for instance, the graviton contribution may simply be too weak to be detected.
Cosmic phase transitions
It could be that the universe remained gravitationally smooth and quiet after inflation, with few gravitational waves being generated. On the other hand, inflation could have become unstable as it drew to an end, triggering bulk motions of mass and energy that generated lots of gravitational noise. Gravitational waves therefore provide a unique signature of the physics of this and other crucial phase transitions in the early universe that changed the course of cosmic history.
At the end of inflation the huge internal vacuum energy that drove the expansion is thought to have been converted into normal, non-inflating energy – i.e. thermal radiation in the form of many fast moving particles, some of which went on to become the cosmic microwave background. How this phase transition took place depends on the way the internal vacuum energy of inflation couples to other physical fields, such as those described by the Standard Model of particle physics. Although this coupling is not currently understood, models of inflation suggest that a measurable fraction of the inflation energy can indeed be converted into gravitational noise.
There is no reason to suspect that such phase transitions in the universe were wildly different to those seen every day on Earth. Indeed, inflation may well have ended in a phase transition much like that of water turning from a liquid to a gas. When you boil a kettle, heat is converted from energy in the water to energy in the steam, during which the flow of material is unstable: the steam forms in superheated bubbles of water that grow explosively once they convert to the steam phase, turning a tranquil pool of hot water into rolling turbulence. In the early universe a similar instability can be powered by supercooling from the cosmic expansion.
Phase transitions are not new in cosmology. As long ago as 1949 Maria Mayer and Edward Teller wrote a paper about stellar-mass lumps of neutron-rich material formed in a cosmological nuclear phase transition. Today physicists use the Standard Model and particle accelerators to probe nature at still earlier times – and hence higher energies – in cosmic history. Phase transitions are a key part of the Standard Model and its various extensions. For example, quantum chromodynamics – the part of the Standard Model that describes how quarks interact by exchanging gluons – is often associated with a phase transition that takes place at an energy of several hundred mega-electron-volts, whereby the “hadronic” phase of familiar nucleonic matter (e.g. protons and neutrons) emerges from a “quark soup” phase of free quarks and gluons.
At the much more energetic tera-electron-volt (1012 eV) scale of the early universe, the vacuum is thought to have undergone a transition from a “false” vacuum (corresponding to a symmetric universe in which all particles are massless) to the “true” vacuum of broken symmetry and massive particles that we observe at today’s low energies. Pinning down the details of this fundamental “electroweak symmetry breaking” process, with which is associated the famous Higgs boson, is the primary goal of the Large Hadron Collider (LHC) at CERN due to switch on early next year.
The idea of searching for gravitational waves from these QCD and electroweak cosmological phase transitions dates back to papers by Edward Witten of Princeton University and me in the 1980s. Since then, other researchers have linked phase transitions with less well established but cosmologically important physics in the very early universe. For example, in 1993 Andy Cohen of Boston University and David Kaplan and Ann Nelson of the University of California in San Diego, both in the US, suggested that disequilibrium as a result of a phase transition could be partially responsible for the small excess of matter particles over antimatter particles in the universe that we observe today – a critical process about which we have no data aside from the excess itself.
Another fascinating possibility is that a phase transition was responsible for the creation of our 3D space some time in the first few trillionths of a second of the universe. In the 1990s string theorists discovered that our 3D world can be described merely as a 3D “brane” of Standard Model fields that lives within a higher-dimensional space. Shortly afterwards, I suggested that the stabilization of our brane as a result of a phase transition from a different configuration in such brane cosmologies could produce an observable gravitational-wave background – effectively providing a test for a particular version of string theory.
Last year, Lisa Randall at Harvard University and Geraldine Servant at CERN worked out a concrete model of such brane-stabilization dynamics that predicts a very strong transition from a primordial higher-dimensional phase to a “Randall–Sundrum brane phase”, and with it gravitational radiation that would be easily detectable with LISA. As is typical of many such phase transitions, the gravitational-wave spectrum displays a peak at a frequency close to the redshifted horizon size, which is the scale at which the most violent cosmological activity takes place, with a broad power law at higher frequencies from smaller scale motions and at lower frequencies from slower, decaying motion.
Quiet universe
The existence of cosmic phase transitions and their possible gravitational signatures therefore suggests that the early universe may not have been the quiet place it is usually assumed to have been. In all these examples of phase transitions, the energy liberated in the process of settling into a new, lower-energy state is released first in the form of bulk motion and only later does it thermalize into microscopic particle motions. By using gravitational waves to infer the critical temperature or “boiling point” of such transitions and their latent heat we can therefore study cosmic processes that are hard to measure in any other way.
Whether or not we can actually detect the gravitational waves produced by such phase transitions depends on their frequencies and amplitudes. The frequency of the waves is set by the time it takes typical bubbles of “cosmic fluid” to collide, while their amplitude is determined by the size of the bubbles and the speed with which they collide. Both frequency and amplitude are thus determined by the typical separation of bubbles, which can be estimated via general thermodynamic principles from the critical temperature and latent heat without knowing the detailed physics of the transition.
For example, we expect bubble nucleation to grow quickly as the universe cools below the critical temperature of the transition and to stop when the separation between bubbles it is at most a few per cent of the size of the universe at the time of the transition. The efficiency with which energy is converted into gravitational waves, which determines their amplitude, has also been estimated to be about 1% or less. This might sound very small, but since gravitational radiation is redshifted by the expansion of space just like ordinary light, it suggests there could be an additional, noisy gravitational-wave background with an energy density just 100 times less than that of the cosmic background radiation. This is comparable to the amount of starlight in the entire universe.
The frequency of the gravitational-wave radiation depends on when the phase transition happened. The wavelength now is its original wavelength (i.e. about 1% of the size of the universe as it was then) stretched by the amount the universe has expanded since then. For example, the electroweak phase transition has a “bubble scale” of about a millimetre – which is actually not too different from that of the bubbles inside your kitchen kettle – so that is the typical wavelength of the noisy gravitational waves when they were created. Once it has been redshifted to the present day, the wavelength of these gravitational waves is stretched to an enormous 100 million kilometres. This corresponds to a frequency in the millihertz range, which we ought to be able to detect with an interferometer such as LISA (figure 5).
Cosmic symphony
Viewed in terms of gravitational radiation, the early universe provides a powerful physics laboratory that complements particle accelerators such as the LHC. The conditions in the early universe at TeV energies will be comparable in energy to the proton–proton collisions at the LHC, but the cosmic system “lasts” for much longer than the LHC collisions and involves many more particles. Indeed, in terms of phase transitions, which involve the collective effect of many particles, the early universe provides an even better laboratory than the LHC!
Phase transitions and inflation are not, however, the only ways to create strong gravitational-wave backgrounds. Physical theories that go beyond the Standard Model – namely string theory – include exotic structures such as branes and strings in addition to the usual particles and fields. At the microscopic scale of atomic nuclei, string-like behaviour has already been inferred in the way that the strong force binds protons together. But it is possible that much longer stable strings exist, rather like long, thin cyclones in the vacuum.
Such “cosmic strings” – if they exist – could have formed abundantly in the early universe as defects at the end of the inflationary phase transition and then stretched to astronomical size by cosmic expansion, losing energy mostly by emitting gravitational waves. Sometimes they may even crack like whips and make a distinctive snapping gravitational-wave “sound” – a phenomenon that Thibaud Damour at the Institut des Hautes Etudes Scientifique in Paris and Alex Vilenkin at Tufts University in the US have recently suggested would provide telltale signs that strings exist.
The properties of cosmic strings are already constrained by the gravitational waves they produce. For example, the mass per length of cosmic strings must be less than about 10–9 in dimensionless units, otherwise their gravitational-wave background would have been detected by now. In fact, this constraint on gravitational-wave backgrounds does not come from interferometers but from the timing of pulses from distant millisecond pulsars. Like giant flywheels, these distant rotating neutron stars slow down at such a stable rate that you can predict the steady arrival time of pulses with an accuracy of about a microsecond per decade. (These pulses are also used to track orbital changes in the system due to gravitational radiation – the discovery of which provides the best evidence of gravitational waves so far and led to the 1993 Nobel Prize for Physics for Russell Hulse and Joseph Taylor.) The apparent stability of such pulsar signals would be disrupted if there were such a cosmic gravitational-wave background. When LISA launches a decade or so from now, however, the limits on cosmic strings will get very much better and perhaps we will actually detect gravitational noises from them.
Detecting cosmic strings from their gravitational radiation would tell us a great deal about how fundamental physics fits together. Cosmic strings have descriptions both in terms of string theory and quantum field theory, displaying aspects of both that remain hidden in the particles and fields so far discovered. That is potentially important as physicists are on the lookout for concrete links between string theory and the known particles and fields, and how these connect to a quantum theory of gravity. As string theory enters its third decade it is more important than ever to connect these beautiful mathematical ideas with real experimental data. The new science of gravitational waves might therefore reveal, in addition to precise and detailed maps of black-hole behaviour, signatures of new fundamental physics.
At a Glance: Gravitational-wave background
- A key prediction of general relativity, gravitational waves are generated when a massive system such as a binary star accelerates and changes shape
- Although there is indirect evidence for gravitational waves, several large interferometers worldwide are currently poised to make the first direct detection
- Gravitational waves squeeze and stretch space–time as they propagate, carrying information about the early universe from long before electromagnetic waves could propagate
- Subtle gravitational-wave signatures in the polarization of the cosmic microwave background could tell us how quickly the universe expanded during inflation, while cosmic phase transitions may have left a gravitational-wave background of their own
- Gravitational waves produced by cosmic strings would connect string theory with the known particles and fields, and help in the quest for a quantum theory of gravity
More about: Gravitational-wave background
T Damour and A Vilenkin 2005 Gravitational radiation from cosmic (super)strings: bursts, stochastic background and observational windows Phys. Rev. D 71 063510
M R DePies and C J Hogan 2007 Stochastic gravitational wave background from light cosmic strings
C J Hogan 2000 Gravitational waves from mesoscopic dynamics of the extra dimensions Phys. Rev. Lett. 85 2044
C J Hogan 2006 Gravitational wave sources from new physics
C J Hogan 2006 The sounds of spacetime American Scientist 94 534
L Randall and G Servant 2006 Gravitational waves from warped spacetime
E Witten 1984 Cosmic separation of phases Phys. Rev. D 30 272