They may look like simple oil drops, but they evoke many of the strange features of quantum theory. Coincidence? Jon Cartwright investigates

Waves can be particles, and particles can be waves. Scientists have struggled to come to terms with this strange feature of the quantum world ever since the French physicist Louis de Broglie first described wave–particle duality in 1926. Are entities waves and particles at the same time – “wavicles” maybe? Or do they switch somehow, depending on the situation? The nature of wave–particle duality seems impossible to understand, because no-one has ever observed something being both a particle and a wave in the everyday world.
At least, that’s what physicists thought. In 2005 Yves Couder and Emmanuel Fort at Paris Diderot University discovered an odd phenomenon. If they placed an oil bath on a vertical vibrator, any oil droplets released onto the surface would not coalesce with the rest of the fluid, as you would expect. Instead the droplets would bounce up and down – their impact cushioned by a pocket of air – while generating circular standing waves.
Adjusting the amplitude of the vibrations, Couder and Fort noticed something even stranger happening. The droplets began to fall onto the wave crests in such a way that they were propelled across the surface. They bounced off the sides of the bath and one another, but always at a distance and never coming into direct contact. It was as though the waves were guiding the droplets to perform an elegant dance – to flit past and spin around one another, but never to collide.
These wave–droplets – or “walkers”, as the researchers began to call them – appeared to be the first macroscopic example of wave–particle duality. The waves could not exist without the droplets, nor could the droplets move without the waves. When a droplet eventually sunk, its corresponding wave would vanish; similarly, if a wave was damped, the droplet would stop moving around the oil bath. Eight years on, Couder and Fort have discovered more and more ways in which their walkers can reproduce phenomena previously considered unique to quantum mechanics – from quantized orbits, to single-particle interference in a Young’s double-slit experiment. The similarities are so marked that many researchers have begun to question whether there could be more to it than mere coincidence. Could a simple, classical experiment reveal something about how the quantum world ticks, and even lead to a deeper theory? “I find these results really, really fascinating,” says Aephraim Steinberg, an experimental quantum physicist at the University of Toronto in Canada. “And I think many people should find them striking.”
Walk the walk
The physics of these wave–droplet interactions may seem complex, but the basic “walking” phenomenon is easy to grasp. If the amplitude of the bath vibrations is just right, the droplet will fall onto the side of a wave crest, bouncing off at an angle. The droplet takes a parabolic trajectory through the air and falls on the side of another wave crest, again bouncing off at an angle and repeating the cycle (see figure 1).
One of the first experiments Couder and Fort tried to perform was the double-slit experiment, which is famous in quantum mechanics for demonstrating the existence of wave–particle duality. Traditionally this experiment is performed with light: a laser beam is sent through two slits in a plate, and the resulting pattern is projected onto a screen behind. The pattern reveals light and dark patches, suggesting that the diffracted light from one slit is interfering, like a wave, with that from the other. However, the same wave-like interference pattern can be built up slowly even when only one photon is sent through at a time.

Couder and Fort’s version of this experiment, which they performed in 2006, uses the same basic arrangement, but with walkers instead of photons and with the plate with double slits partially submerged in the oil bath. The researchers launched walkers towards the plate: if a walker arrived at the plate itself, the walker’s wave component was damped, and the walker either stopped or was reflected. If, on the other hand, a walker arrived at one of the plate’s two slits, it passed through and the researchers measured its subsequent trajectory (see figure 2).
Once a walker had passed through a slit, its direction appeared to be random and had no correlation with its previous trajectory. Upon counting the final trajectories of more than 70 walkers, however, the researchers found that the walkers were in fact reproducing a characteristic interference pattern. Apparently each walker passing through a slit was interfering with itself, thanks to part of its wave component going through the other slit as well (Phys. Rev. Lett. 97 154101).
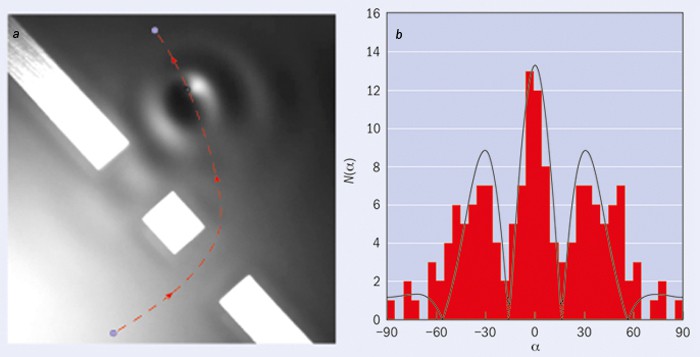
“We were really amazed,” says Fort. “In any first-year undergraduate course on quantum mechanics you look at this experiment, and you try to think of a classical system that does the same, but there is none. So this was really a discovery.”
The success of their double-slit experiment inspired Fort and Couder to try some other experiments reminiscent of those in quantum mechanics. They placed walkers inside baths, and tried confining them in square enclosures with submerged barriers of different widths. Mostly, the walkers bounced around the smaller enclosures like billiard balls. In 2009, however, the researchers discovered that, with a certain small probability, the walkers could “tunnel” across the barriers. During this tunnelling process the droplets skimmed over a barrier, and once they were over, their corresponding wave reappeared and the walkers continued as normal.
The range of quantum effects that the bouncing-drop experiments reproduce is truly remarkable
In quantum mechanics, tunnelling arises from the Heisenberg uncertainty principle. For instance, an alpha particle may not have enough energy, classically, to escape an atomic nucleus, but there is still a chance it will escape thanks to the innate uncertainty in its position. Whereas the properties governing tunnelling in quantum systems are barrier thickness and particle energy, in the Paris group’s system they were barrier thickness and walker velocity (Phys. Rev. Lett. 102 240401).
The following year, Couder and Fort discovered yet another analogy between their walkers and quantum mechanics. Placing the vibrating bath on a rotating pedestal, they found that after a while the walkers began to orbit the centre of the bath – and only at certain radii. It turned out that the walkers’ angular momenta were quantized, in the same way angular momentum is quantized for charged particles orbiting in a magnetic field in so-called Landau quantization. Simulations performed by the Paris group suggested that the quantization arose because of past waves emitted by the walkers, which over time built up into a wave field that guided the walkers into certain orbits (PNAS 107 17515).
De Broglie’s mechanics returns
Many physicists agree that Couder and Fort’s walkers are the first classical example of De Broglie’s wave–particle duality. But some go further and argue that the walkers appear to implement De Broglie’s picture of quantum physics itself. De Broglie believed that particles really exist, and are guided by equally real “pilot waves” that force them to adhere to quantum statistics. The pilot waves in De Broglie’s picture make nature deterministic, although they operate in a nonlocal, faster-than-light manner (see November 2009, pp32–37).
The ease of performing walker experiments has led several groups over the world to try them out. Among them, a small minority believe the walkers are directly mirroring what is going on in the quantum world. “I strongly believe this is not a coincidence,” says mathematician Aslan Kasimov at the King Abdullah University of Science and Technology in Saudi Arabia. “The range of quantum effects that the bouncing-drop experiments reproduce is truly remarkable, and should serve as a strong indication that a similar mechanism exists in quantum mechanics.”
Couder and Fort do not share such unbridled optimism, pointing out that the walkers’ analogy with quantum mechanics fails in many respects. From an experimental point of view, one difference is obvious: their system is dissipative, so without an energy input in the form of bath vibrations the walkers simply disappear. Another difference is that the Planck constant – so important for describing the innate “granularity” of the quantum world – cannot so far be derived from walker observations.
Perhaps the most important difference, however, regards the form of the walker’s associated wave. In quantum mechanics, a pilot wave or a wavefunction exists in a mathematical space of 3N dimensions, where N is the number of particles in a system. Even if a system contains just two particles, that means six dimensions – and the dimensionality rises swiftly as the system gets more complicated. In a walker system, regardless of how many walkers are present, the number of dimensions occupied by the waves is always just two, given by the length and width of the oil surface.
This contrast in dimensionality is more than just a technical detail. In quantum mechanics, it is the dimensionality of the wavefunction that is responsible for the weirdest quantum phenomenon of all: entanglement. Without a highly dimensional wavefunction, many physicists argue, it is impossible to explain how entangled particles can affect one another over large distances, faster than the speed of light. Such nonlocality in quantum mechanics has been demonstrated since the experiments of the French physicist Alain Aspect and others in the early 1980s, based on earlier theoretical reasoning by the Northern Irish physicist John Bell.
The disanalogies between the walker system and the pilot-wave theory are just as important as the analogies
“When there is more than one particle, the pilot wave, or quantum wavefunction, is not a function of physical space, and so cannot be analogous to any water or oil wave,” says philosopher Tim Maudlin at New York University in the US. “This allows for the entanglement of a pair of particles, and all of the effects of entanglement. If one thinks of this behaviour as central to quantum theory, it cannot possibly be reproduced in the [walker] system.”
Indeed, Physics World contacted a number of physicists and philosophers with a background in quantum foundations, and found that most were sceptical that the walker systems could shed light on the mysteries of the quantum world. “The reproduction of two-slit interference is impressive,” says philosopher Peter Lewis from the University of Miami in Florida, US, “but I think the disanalogies between the [walker] system and the pilot-wave theory are just as important as the analogies, and perhaps more so.”
A lesson from gravity
Most were sceptical – but not all. One exception was theoretical physicist Antony Valentini at Clemson University in South Carolina, US, who points out that walker systems are not the first to present strong analogues of a hard-to-grasp theory: the last decade has seen numerous experimental attempts to produce analogues of gravity, using fluids and light. “People are now wondering if we should look at these [analogue gravity] models and use them for inspiration when we’re looking at how our current theories of gravity might break down at short distances,” he says.
Analogue gravity models took a long time to catch on since their original theoretical proposal in the early 1980s by the Canadian physicist William Unruh. In the same way, says Valentini, it might take a while for Couder and Fort’s walker systems to inspire those studying quantum foundations in searching for a deeper theory.
Valentini stresses that the walkers will not be able to exhibit true, faster-than-light nonlocality. But what if the Paris researchers discover that the dynamics of their oil bath is governed by a characteristic speed – a speed much less than, but analogous to, the speed of light? Then, suggests Valentini, it would not be too much to imagine that the walkers might affect one another faster than this characteristic speed, analogous to how entangled microscopic particles are able to affect one another faster than the speed of light.

“Such a [situation] might encourage people to think that the nonlocality we observe in the lab isn’t instantaneous, isn’t infinitely fast,” Valentini adds. “That it’s much faster than light, but still finite.” As such, he believes the walkers might give us clues as to where quantum mechanics might break down.
There is already good reason to think that the walkers might exhibit some sort of pseudo nonlocality. Fort and Couder find that the dynamics of walkers is governed largely by the “memory” of past waves, which gradually builds up over the oil bath into a wave field. In this way, the Paris researchers say, one walker can seem to nonlocally affect another walker on the other side of the bath, thanks to a wave – or combination of waves – it emitted previously. This “memory” effect was key to the observed quantization of walker orbits on a rotating oil bath. This year, the researchers demonstrated the memory effect in a more general sense: if a walker is left long enough, its trajectory becomes “entangled” with a wave field in the bath.
Curiouser and curiouser
Will Fort and Couder’s walkers inspire physicists to find a theory deeper than quantum mechanics? It may be too soon to tell, but one point does seem clear: every time they look, the researchers find more ways in which walkers exhibit supposedly quantum behaviour. In another paper published this year, for instance, they present a macroscopic analogue of a so-called quantum corral (Phys. Rev. E 88 011001). In surface physics, a quantum corral is a ring of atoms that pens in, or “corrals”, the wavefunctions of electrons held within into certain modes. Fort and Couder find that, in a classical, circular enclosure, walkers tend to occupy positions that match these quantum modes (see figure 3).
Mathematician John Bush at the Massachusetts Institute of Technology in the US, who collaborated with Fort and Couder on the quantum-corral study, recalls when he first listened to a talk on walkers. “Some of my colleagues were very dismissive; they thought it was just a coincidence,” he says. “But once you’ve heard of De Broglie’s mechanics, and you realize that these experiments are basically a macroscopic realization of it, and that they give quantum-like behaviour – it seems like too much of a coincidence. And so when I heard about it, I basically went all in!”



