Why can climbing plants twine around thin canes, but not around trees? This question has been playing on the minds of mathematicians in the US and France, who now claim to be able to predict the "critical radius" of the pole that a plant can climb (Phys. Rev. Lett. 97 184302).
Climbing plants have developed many different techniques for growing vertically upwards without being able to support themselves. Garden peas, for example, grow by wrapping themselves in a spiral around an appropriate upright support. Alain Goriely from the University of Arizona and Sébastien Neukirch from the Université Pierre et Marie Curie have now modelled this process by assuming that a plant’s tendril is akin to an elastic rod wrapped around a cylindrical pole. The two researchers were then able to calculate the positions of the tendril where the tension in the stem is balanced by the resultant force from the support.
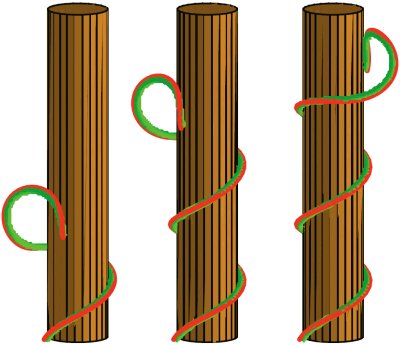
They discovered that the tendril’s natural curvature plays a crucial role in determining the radius of the pole that it can climb. For relatively thin poles, the tip curls closely around the surface – in other words, the angle between the tip of the tendril and the tangent of the pole is almost zero. For a slightly thicker pole, the tip must curl into the pole’s surface to maintain its grip, so the angle increases. When the radius of the pole is more than 3.3 times the tendril’s natural curvature, the angle increases so much that the tip curls back on itself, leaving the tendril unable to climb at all.
Goriely and Neukirch went on to study how important friction was for climbing. Unsurprisingly, friction helps tendrils to climb by preventing the tendril from sliding back. In fact, they reckoned that if the friction is high enough, plants could climb poles up to eight times the tendril’s radius.