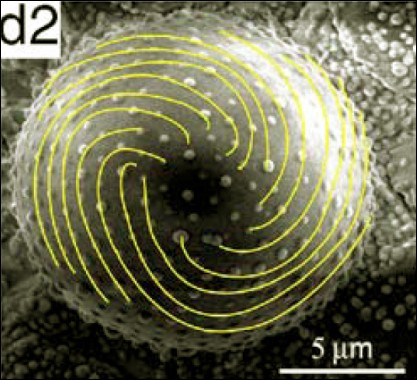
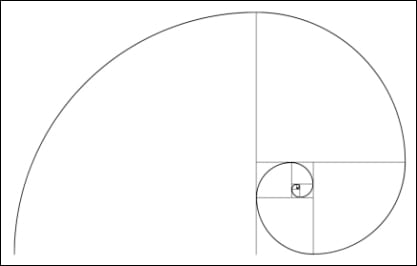
The Fibonacci sequence -- in which each successive number is the sum of its two preceding numbers -- regularly crops up in nature. It describes the number of petals around daisies, how the density of branches increases up a tree trunk, and how a pine cone's scales are arranged. Now, having performed "stress engineering" to create Fibonacci-sequence spirals on microstructures grown in the lab, physicists in China think they may have found the reason why the sequence is so ubiquitous -- with a little help from a seemingly unrelated physics problem posed over 100 years ago (Appl. Phys. Lett. 90 164102).
spiral
Stress engineering can be used to create microstructures without using any high-precision patterning equipment. In the technique, a curved “core” material is coated with a different “shell” material at a high temperature. The composite is then cooled while carefully restricting the geometry, and because of difference in the thermal expansion of each material selective parts of the shell buckle under stress, causing patterns to form.
Zexian Cao and colleagues from the Chinese Academy of Sciences used stress engineering to create different-shaped microstructures just 12 µm across with a silver core and a SiO2 shell. They discovered that if the shells were encouraged into spherical shapes during cooling, triangular stress patterns formed on the shells. On the other hand, if they were encouraged into conical shapes, spiral stress patterns were formed. These spiral patterns were “Fibonacci spirals” – that is, spirals that have dimensions governed by the Fibonacci series (see fig: “Fibonacci spiral”).
Cao’s team do not think the Fibonacci spirals formed by accident, however – they think that their cause may be related to a tricky problem posed by the physicist J J Thomson in 1904. Thomson asked how a collection of like-charges would arrange themselves on a conducting sphere so as to minimize energy. Physicists have since calculated that the charges would take on triangular patterns – similar to Cao’s spherical microstructures. Because of this, Cao’s team thinks that the Fibonacci spirals on the conical microstructures must be the equivalent minimum-energy (and hence minimum-stress) configuration for a cone, although they have not performed any calculations themselves.
Biologists have long suspected that the branching of trees and other occurrences of the Fibonacci sequence in nature is simply a reaction to minimize stress, but no concrete proof of it has every been found. “Our experiment using pure inorganic materials may provide proof to this principle,” Cao told Physics Web.
Cao added that using stress engineering to create Fibonacci patterns could also have applications in photonics: “Fibonacci spirals are a special lattice; I would say they are both ordered and disordered. If the lattice points were some materials of a proper ‘dielectric’, it may provide a new photonic crystal that displays some interesting properties.”