Physicists in the US have gained important insights into the process of crystallization by studying how tiny plastic balls spontaneously form clusters. They found that highly symmetric clusters are created much less often than those with lower symmetry, which could shed light on how clusters of atoms or molecules form just before a liquid solidifies into a crystalline solid.

The conventional view of crystallization is that a material solidifies when one or more of these tiny clusters grows past a point of no return. But while the energies of possible cluster shapes can be calculated and confirmed experimentally, understanding the role that entropy plays is much harder. In an isolated system, for example, thermodynamics favours the formation of disordered clusters (i.e. those with a high entropy) – provided that the energy of these clusters is low enough that is.

The problem is that actually observing the role of entropy during crystallization is difficult because the clusters are too small and appear and vanish much too quickly to be seen. But by using clusters of much larger particles, which can be observed in real-time with an optical microscope, Vinothan Manoharan and colleagues at Harvard University in the US have been able to gain new insight into the role of entropy in the “nucleation” process.

Maximizing entropy

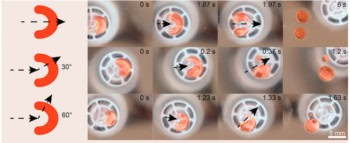
The team began with an array of thousands of tiny wells on a silicon chip – each well having a depth and diameter of 30 µm. The wells are filled with a mixture of water and two types of plastic balls – one type with a diameter of 1 µm and the other 80 nm. Both types of ball are jostled about by random thermal fluctuations in the water (Brownian motion).

However, when two large balls come to within about 80 nm of each other, the small balls can no longer fit between them. Because there are no small balls between the large balls to push them apart, the balls start to close in on each other. This imbalance looks like a short-range attractive force that causes the large balls to stick together in clusters – the so-called “depletion attraction”.

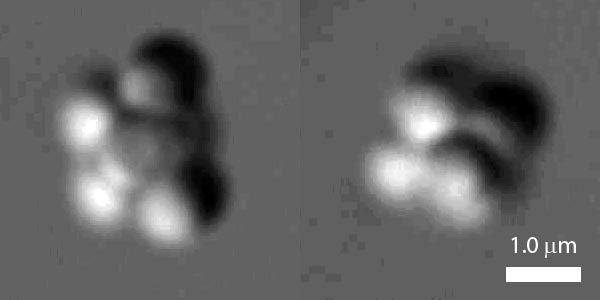
The team began by looking at wells containing six large balls. These tend to form clusters with either a symmetrical octahedron shape or a less symmetric complex of three tetrahedrons. Although both shapes have 12 bonds between balls, which means that they have exactly the same energy, the high-entropy tri-tetrahedron was found to be about 20 times more common than its more symmetric counterpart.

‘Ball-and-stick’ analysis

To understand why the tri-tetrahedron was more common, the physicists used a magnetic “ball-and-stick” construction toy to work out all the possible ways that the two different clusters could be oriented. From rotational-entropy considerations alone, the team expect the low symmetry tri-tetrahedron clusters to be 12 times more numerous that the octahedrons.

Although this is not the factor of 20 observed experimentally, the team believes that the remaining factor of about two can be explained in terms of vibrational entropy. The tri-tetrahedron is less rigid than the octahedron, which means that the tri-tetrahedron can flop about between different configurations – further boosting its entropy.

The researchers then turned their attention to larger clusters of up to 12 balls and found that the clusters also favoured the least symmetric and least rigid configurations. Indeed, at 12 balls the most symmetric (and least energetic) structure was never observed. As a result, most of the larger clusters looked like familiar bulk-crystal structures such as hexagonal-close-packed.

Although the study illustrates the importance of symmetry in the formation of tiny clusters, Manoharan points out that crystallization involves long-range interactions between atoms that are not reproduced by the depletion attraction. When such interactions are considered in the team’s model, the effect of entropy is not as strong. Also, the studies were done in complete isolation where the clusters could come to equilibrium without being disturbed by their surroundings, which does not apply to most real systems.

The work is reported in Science.