Magnetic interactions usually seen deep within solid materials have been simulated for the first time using ultracold atoms. By “tilting” a 1D chain of atoms, physicists in the US have created a structure that resembles a quantum antiferromagnet. The researchers say that the technique could be extended to 2D lattices of atoms and could provide important insights into the nature of magnetism.
For the past decade or so, physicists have been using lasers and magnetic fields to trap collections of atoms and cool them to temperatures near absolute zero. By carefully manipulating the laser light and magnetic fields, researchers can control the interactions between atoms – allowing them to simulate interactions that occur between electrons or ions in solid materials. But unlike solids, the strength of these interactions can be easily adjusted, allowing physicists to test theories of condensed-matter physics in these “quantum simulators”.
In this latest simulation, Markus Greiner and colleagues at Harvard University begin with a cloud of rubidium-87 atoms that they cool to less than 100 pK. Then they fire a laser at a holographic mask to create a 1D optical lattice, which is a string of about 100 alternating bright and dark regions repeating every 680 nm. The atoms arrange themselves at regular distances with each dark region – or “well” – containing exactly one atom. Although an atom could tunnel through the light region to join its neighbour, it is discouraged from doing so by the high energy cost of two atoms occupying one well. This state of matter is known as a Mott insulator and has already been studied extensively using ultracold atoms.
Paramagnetic state
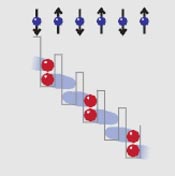
An atom occupying its original well can be thought of as a magnetic moment pointing “up” and an atom that has tunnelled to the neighbouring well as a moment pointing “down”. A Mott insulator, therefore, is an analogue of a paramagnetic state in which an external magnetic field forces all of the magnetic moments in a material to point in the same up direction.
The team then “tilt” the lattice by applying a magnetic field gradient to the atoms, which encourages the atoms to move in one direction along the string. If the tilt energy is greater than the interaction energy, then every second atom tunnels into its neighbour’s well – resulting in alternating wells with zero and two atoms, respectively. According to Greiner, this can be mapped directly onto a 1D antiferromagnet – an arrangement of spins that point up and down in an alternating pattern.
By adjusting the relative strength of the tilt and interaction energies, the team mapped out the transition from the paramagnetic to antiferromagnetic phases. This occurs via a quantum phase transition when the tilt and tunnelling energies are equal. At the transition point, quantum fluctuations in the positions of the atoms grow rapidly, driving the system from one configuration to another. Such quantum fluctuations correspond to individual spins simultaneously pointing in different directions – a quantum superposition. This situation could never occur in the world of classical physics, but gives rise to fascinating properties of quantum magnets.
Ising on the cake
The effective interaction between up and down moments depends on whether a well’s two nearest neighbours are occupied. As a result Greiner and team have simulated the “quantum Ising model” – which provides a simple yet useful explanation of magnetism.
Greiner told physicsworld.com that the team’s next step is to look at excitations in the system. “We can flip a single moment and see what happens,” he said. Gaining a better understanding of such excitations could provide important insights into real magnetic materials.
The group also plans to simulate antiferromagnetism in 2D by placing ultracold atoms in a 2D optical lattice. By studying a triangular lattice, for example, the team could gain insight into “frustrated” magnetic systems, in which a moment cannot minimize its energy with respect to all of its nearest neighbours.
The research is reported in Nature 10.1038/nature09994.