Physicists in the US, India and China have calculated that quarks and gluons can break free from their confinement inside protons and neutrons at a temperature of around two trillion degrees Kelvin – the temperature of the universe a fraction of a second after the Big Bang. The researchers arrived at this figure by combining the results of supercomputer calculations and heavy-ion collision experiments. They say that it puts our knowledge of quark matter on a firmer footing.
According to the Big Bang model, the very early universe was filled with “quark–gluon plasma”, in which quarks and gluons (the carriers of the strong nuclear force) existed as individual entities. The strong force between quarks increases rapidly with distance, which means that the quarks need large amounts of energy to remain free – and therefore the plasma can only exist at extremely high temperatures. When the cosmos was only about a millionth of a second old, it had cooled to the point where quarks and gluons combined to form composite particles such as protons and neutrons. Exactly what this temperature is, however, has not been easy to work out.
The theory of quantum chromodynamics (QCD) explains the interactions of quarks and gluons extremely well at very small distances, which are relevant in the collisions taking place inside the Large Hadron Collider (LHC) at CERN in Geneva. But at the larger distances characteristic of the quark–gluon plasma, QCD fails because it becomes impossible to account for all of the constituent interactions, which include many virtual pairs of quarks and antiquarks. So physicists use an approximation of the theory known as lattice QCD, in which the complexity of quark–gluon interactions is limited by breaking down space–time into manageable chunks.
Anchoring lattice QCD
Now Nu Xu of the Central China Normal University and the Lawrence Berkeley National Laboratory in California and colleagues have anchored the value of one of the key parameters of lattice QCD. They used results from the STAR detector at Brookhaven Laboratory’s Relativistic Heavy Ion Collider (RHIC), which collides gold ions together at high energies to work out the temperature at which the quark–gluon plasma “condenses” to form individual hadrons.
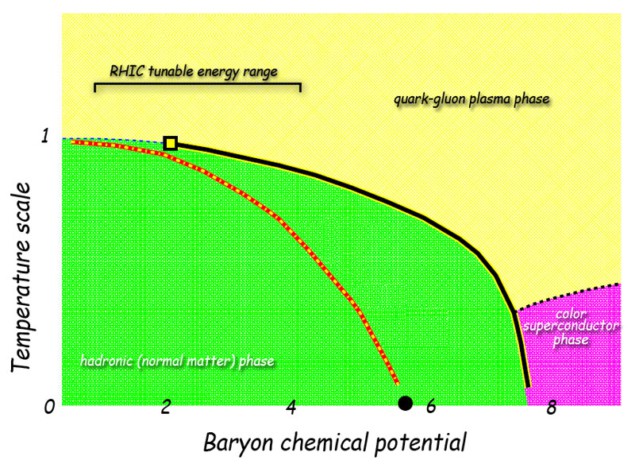
Team member Bedangadas Mohanty of the Variable Energy Cyclotron Centre in Kolkata, India, explains that knowing this temperature helps to map out the phase diagram of QCD. This diagram charts the transition from normal, hadronic, matter to quark matter (or possibly to another exotic state known as “colour superconductivity”) as two variables are altered. These are the temperature and “baryonic chemical potential”, the latter being the energy needed to remove or add a proton or neutron to the strongly interacting matter. He points out that thermodynamics can be used to work out how the temperature of water’s phase transitions varies with pressure but that absolute values for these temperatures require the measurement of at least one fixed point within the phase diagram, say the boiling point at atmospheric pressure. “Likewise,” he says, “in QCD we want to find out what is the temperature of the phase transition at zero chemical potential.”
Calculating susceptibilities
Xu and co-workers didn’t measure this temperature directly but derived it from theory and experiment. On the theoretical side, Sourendu Gupta and others at the Tata Institute of Fundamental Research in India calculated the first, second, third and fourth derivatives of the baryonic chemical potential with respect to pressure, and then worked out how these “susceptibilities” should vary with temperature. Meanwhile, the experimental half of the collaboration counted how many more protons than antiprotons were produced in millions of collisions of gold ions at RHIC and plotted the variation in this measured quantity. At the quark–gluon plasma transition temperature, certain combinations of the theoretical susceptibilities should numerically equal particular quantities relating to the shape of the measured distributions. So, by varying the susceptibilities with temperature until they equalled the quantities derived from experiment, the researchers arrived at a value for the transition temperature.
The value obtained by Xu’s team was 175 +1/–7 MeV, equivalent to 2 × 1012 Kelvin, which is exactly the value predicted by other indirect methods in lattice QCD. “This is the first time that there has been a direct comparison between high-temperature quark-matter theory and high-energy experiments,” says Mohanty. “People have predicted what the theoretical susceptibilities should be, but you need to compare these predictions with experiment to be sure that the theory is correct.”
Finding a critical point
The next step, adds Mohanty, is to measure a predicted critical point within the QCD phase diagram. At a critical point, a boundary between two phases comes to an end and the properties of the two phases become identical. There is a critical point for liquid water and steam, for example, and nuclear physicists believe that likewise there is one for normal and quark matter. Finding this critical point will involve carrying out heavy-ion collisions over a range of collision energies, something, says Mohanty, which RHIC is ideally suited to do. The LHC’s ALICE detector, on the other hand, should be able to nail down the quark–gluon plasma’s viscosity, with previous measurements having suggested that the plasma has a lower viscosity than any other liquid in the universe.
David Evans, a physicist at Birmingham University and head of the UK group at ALICE, is impressed by the latest work. “I think these techniques will allow theorists to tune up and improve lattice QCD by direct comparisons with experiment,” he says, “and hence provide even better calculations and predictions in the future.”
However, Johann Rafelski of the University of Arizona believes that the research suffers from “major deficiencies”, in particular a lack of analysis of systematic errors. For example, he says, Xu and colleagues have not accounted for the fact that the detector counts only a limited fraction of all collision products. “The total systematic error is very probably much, much larger than the statistical error [as presented],” he says, adding that his “colleagues from the lattice-QCD community believe that this analysis has `errors at every step'”.
The research is published in Science 332 1525.



