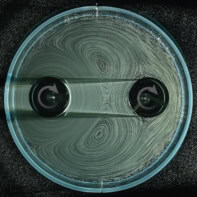
An international team of scientists has demonstrated for the first time that a special kind of wave structure – a dark soliton – can be produced in water. Like the bright soliton – which is thought to be responsible for amplifying ocean waves to “rogue wave” proportions – the dark soliton is a localized surface “wave envelope” that causes a temporary decrease in wave amplitude.
Unlike typical ocean waves, which are always evolving as they ebb and flow, solitons maintain a constant shape and size as they propagate. They typically travel slower than background waves, which get modulated as they pass through the soliton and return to their original amplitude as they re-emerge.
The terms bright and dark soliton are borrowed from optics, where they manifest as bright spots and dark shadows in optical fibres. And yet it was in water that solitons were first observed, in the 1830s. The discovery in the 1960s and 1970s of bright solitons on the surface of deep ocean waters initially stunned oceanographers, but many experiments have been done to explore and confirm the phenomenon since then, including those that pegged bright solitons as the culprit for seeding rogue waves at sea. Solitons of both the bright and dark persuasions have now been spotted in fibre optics, plasmas, Bose–Einstein condensates and elsewhere. But in all this time, a dark soliton had never been seen in water until now.
Predictions play out
Amin Chabchoub, a mathematician at Imperial College London, and colleagues applied the nonlinear Schrödinger (NLS) equation – the widely accepted model for describing evolving water waves – which has a large family of soliton solutions. There are two forms of the equation: a focusing case, which produces bright solitons and only applies in deep water, and a defocusing case, which governs waves in shallow water and leads to dark-soliton solutions. For this to be the case, kh (the wavenumber multiplied by the water depth) must be less than 1.363.
Chabchoub’s team used a 17-m-long wave tank, filled to a depth of 40 cm. With a computer-controlled paddle at one end of the tank, the researchers generated a steady sine wave with an amplitude of 4 cm and a precise initial surface elevation, according to the defocusing NLS equation. Conductive wave gauges placed at intervals along the tank monitored wave propagation.
As predicted, the researchers witnessed the background waves’ amplitudes falling to zero as they passed through the soliton, only to bounce back to their initial magnitude upon exiting the structure. Not only that, the team’s theoretical predictions about how the width of the soliton – that is, the number of background waves under its influence at any given time – ought to vary with various factors (e.g. deeper water, wider soliton) were also borne out spectacularly well in the data. “We can really say then that they’re really dark solitons, not only from their shape but also that they have these characteristics which are provided by theory,” says Chabchoub.
“New way of thinking”
“This is an exciting result,” says Roger Grimshaw of Loughborough University, who was not involved in the research. “While both versions of the NLS were known to be valid for optics, this is the first time that the same has been shown for water waves. This opens the door to a new way of thinking about nonlinear waves in shallow water, although it is likely that this is only for a limited range of kh.”
The widely accepted model for nonlinear, shallow water waves, where kh approaches zero, is the Korteweg–de Vries (KdV) equation, which has soliton solutions that differ strongly from those described by the NLS equation. “The experiments in this paper are for small, but finite kh – 1.2, 1.0. I doubt that the dark soliton will be found if kh is decreased too much below these values,” says Grimshaw.
Chabchoub says the group’s next priority is to investigate interactions between solitons. “What happens if you collide these guys?” he asks, “or if a dark and bright soliton meet?” It is a line of research that may eventually help engineers design technologies that better mediate destructive waves at the shore. “If there’s a huge wave coming, maybe we can stabilize it or act against it. We don’t know yet,” says Chabchoub. He points out that the team “needs to do numerical simulations to investigate whether these coherent structures could have an influence on tsunamis or on the propagation of high waves, which can be dangerous near shore”.
The research is published in Physical Review Letters.