Fantastical knot-like structures of light could soon be created in the lab thanks to calculations made by physicists in the US, Poland and Spain. They have discovered a new family of solutions to Maxwell’s equations that are knots of light that do not disperse or lose their specific topological properties as they propagate. The researchers say such knots, if made for real, could be used to trap atoms or create similar knots in plasmas or quantum fluids.
Identified by Hridesh Kedia at the University of Chicago, along with colleagues at the Polish Academy of Sciences in Warsaw and the Spanish National Research Council in Madrid, the new family of solutions to Maxwell’s equations have field lines describing all “torus knots” and “links”. Torus knots are those knots that can lie on the surface of a torus, whereas a link is a collection of such knots.
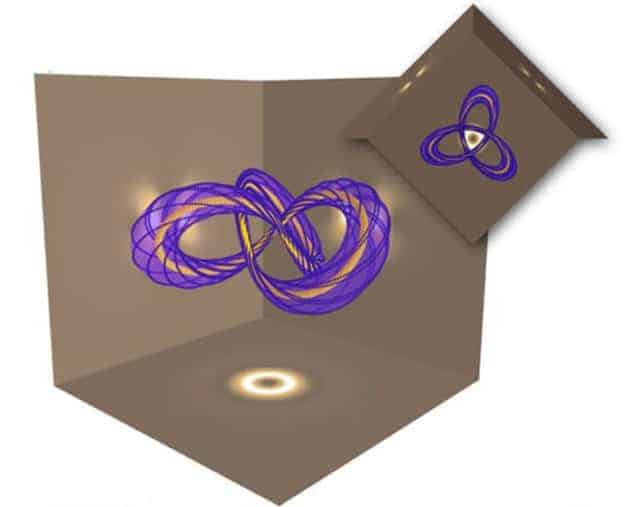
One solution involves magnetic-field lines that trace out a familiar “trefoil” knot around a torus that is aligned in the plane perpendicular to the direction of propagation of the light (see figure). As the light propagates, the knot is distorted but retains the topological property of being a trefoil knot. The electric-field lines have the same structure as the magnetic-field lines but are rotated about the propagation axis by an angle that depends upon the knot. Other solutions include cinquefoil knots and linked rings.
Knotty problem
Kedia and colleagues believe that these knots could be made in the lab using tightly focused Laguerre–Gaussian beams. These beams have been created and studied extensively because – unlike most other beams of light – they carry orbital angular momentum.
If these optical knots can be made in the lab, they could have a number of scientific applications. Physicists are already exploring how focussed Laguerre–Gaussian beams can be used to trap ultracold atoms and this latest theoretical development could lead to new ways of trapping them. Firing such knots into a plasma or quantum fluid could also result in knot-like entities propagating through those materials, thereby offering new ways of studying these states of matter.
Once the preserve of mathematicians, knot theory is playing an increasingly important role in how physicists describe the behaviour of physical systems, ranging from liquid crystals to superconductors. Most of these descriptions arise from numerical simulations of complex systems, rather than the exact solution of the equations describing the system of interest.
The research is described in Physical Review Letters.



