Two physicists in the UK have added further insight into the seemingly paradoxical “quantum-pigeonhole effect”, which says that if three quantum particles are distributed over two locations, certain measurements will reveal that there is just one particle in each location. Alastair Rae and Ted Forgan of the University of Birmingham have calculated that quantum-interference effects can make it appear that each location only holds one particle, even though two particles might actually be present. They warn, however, that measuring the effect in the lab would be an extraordinarily difficult task.
The quantum-pigeonhole effect was introduced last year by Yakir Aharonov and Jeff Tollaksen of Chapman University in the US, together with colleagues in Italy and the UK. It is an extension of the classical pigeonhole principle, which simply says that if n objects are placed in n – 1 different locations (or pigeonholes) at least one location will contain more than one object. The team argued that in quantum physics, making a special sequence of measurements on three quantum particles that had passed through the equivalent of two pigeonholes would apparently reveal that no two particles had been in the same pigeonhole (see “Paradoxical pigeons are the latest quantum conundrum”).
Electron deflections
Tollaksen and colleagues had also proposed an experiment to verify this apparent violation of the pigeonhole principle. It would involve sending three electrons through a Mach–Zehnder interferometer, which contains a beamsplitter that creates two separate paths for the electrons. The three electrons are then brought together at a second beamsplitter before diverging to two different detectors (see the figure below).
As there are only two possible paths, you would expect at least two (and sometimes three) electrons to share a path. These two (or three) electrons travelling together would then be close enough to repel each other, deflecting their trajectories slightly. When all three electrons are detected, these tiny deflections should give a pattern of electron arrivals at the detectors that would reveal that two or more electrons had travelled along the same arm of the interferometer.
Tollaksen and colleagues focused on what would happen if the experiment were run in a certain way that involves only looking at the output of the detector – a process called “post-selection”. Under these conditions, they concluded, an experimentalist would not be able to tell that two electrons had travelled along the same arm.
Possible paths
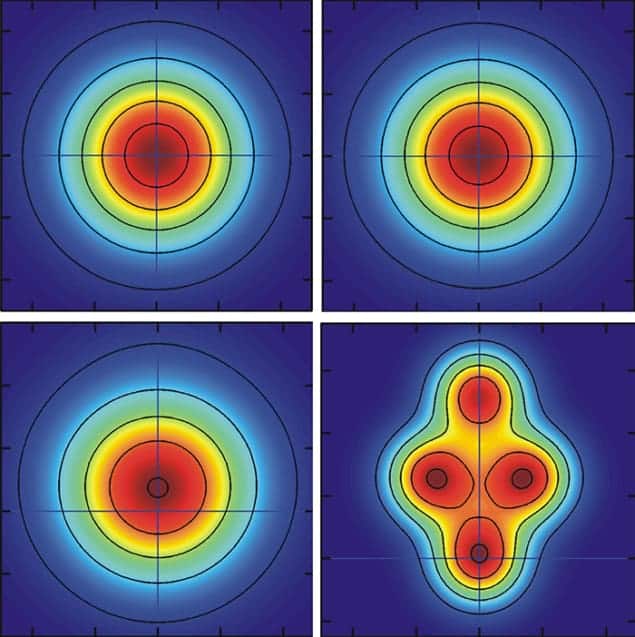
Rae and Forgan have now analysed the outcome of such a hypothetical experiment, and have shown that applying quantum mechanics and the classical pigeonhole principle can explain the apparent paradox. Their calculations involve constructing the quantum-mechanical wavefunction of the three electrons in terms of the possible paths that the electrons can take through the experiment – all three electrons going through one arm, for example, or two electrons going through one arm and one through the other.
They find that if there is a relatively strong interaction between the electrons, you would see 12 spatially separated peaks at the detector, which would be a sign of the classical pigeon principle at work (see figure at the top of the article). In other words, there would be four peaks for each electron, corresponding to the four possible histories of the electron motion: travelling alone, with one or other of the other two electrons, or with both. If the interaction strength were zero, on the other hand, then only three peaks – one for each electron – would be measured in the detector. As expected, such a measurement will yield no information about how many electrons travelled through each arm of the interferometer.
Fooled by interference
Rae told physicsworld.com that things become very interesting when the interaction strength is small but finite. Three peaks would then be seen at the detector, and the pattern resulting from the interference between the four components of the wavefunction (all of which obey the classical pigeonhole principle) will look very similar to that which occurs when the interaction is zero. As a result, the observer might be forgiven for concluding that two or more interacting electrons had travelled through the interferometer without interacting.
Rae and Forgan also looked at whether it would be possible to run the experiment with electrons in the low-interaction-strength regime. Their calculations suggest that for 40 keV electrons, an experimentalist would have to discern patterns in their detectors across distances of about 10–13 m. This is about 1000 times smaller than the distance between atoms in a solid, making the measurement extraordinarily difficult if not impossible, according to the researchers.
The research is described in a preprint on arXiv.




