When most of us think about searching for physics beyond the Standard Model – the dominant paradigm of particle physics – the first thing that springs to mind is probably a gigantic particle accelerator like CERN’s Large Hadron Collider (LHC). Within the collider’s 27-km loop, protons slam together at 99.9999991% of the speed of light. Office-building-sized detectors generate terabytes of data for physicists to sift through, seeking elusive traces of new kinds of particles.

But there is another type of search for new physics under way as well, this time in atomic-physics labs. Using apparatus no more than a few metres in size, and energies a trillion times lower than those at the LHC, these experimentalists are trying to detect new particles, too – by measuring the electric dipole moment (EDM) of the electron.

The logic behind their search is that under the basic Standard Model, a detectable electron EDM is forbidden. Hence, finding a tiny-but-finite EDM would indicate that the Standard Model needs revision, thereby opening the door to a new class of “virtual particles”. From an experimental standpoint, the task is not easy: how do you measure something that is almost, but not quite, zero? Yet these EDM searches may nevertheless be our best chance of discovering new physics until the LHC reaches its full potential – and perhaps even beyond then.

Rules and exceptions

The most familiar example of a dipole is a magnet. If you place a common bar magnet, like a compass, in a magnetic field, its north and south poles will align with the field. Similarly, an electric dipole can be created by placing two oppositely charged objects close together. The electric dipole moment, d_e, of this simple system is equal to the magnitude of the charge, q, multiplied by the charge separation distance, r, i.e. d_e = qr. Like a magnetic dipole, an electric dipole has a direction (both r and d_e are vectors), and it will tend to align itself with an applied electric field. For fundamental particles, d_e is measured in e cm, where e is the charge on the electron (1.6 × 10^–19 C).

Physicists have known since the 1920s that the electron behaves like a magnetic dipole, thanks to its “spin”, or intrinsic angular momentum. (The electron is not literally spinning, but the analogy with a spinning ball of charge is a useful one.) However, as a fundamental particle, the electron should not have a permanent electric dipole moment – at least not according to the simplest version of the Standard Model. The absence of an electron EDM is a consequence of “time-reversal symmetry”, a fundamental principle of physics that holds that physical interactions should look the same if the direction of the flow of time is reversed.

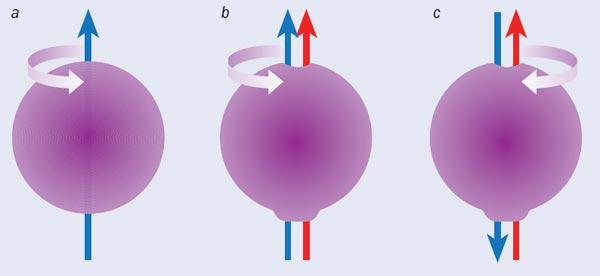
To understand why a permanent EDM for the electron would violate time-reversal symmetry, consider our picture of the electron as a tiny, spinning ball of charge. The spinning charge acts like a small loop of current and produces a magnetic dipole moment along the spin axis (the blue arrow in figure 1a). To produce an EDM, we must distort the charge distribution of the electron slightly, creating an electric dipole along the spin axis (red arrow in figure 1b). When we reverse time, we reverse the ball’s spin, and thus the direction of the magnetic dipole. But the charge distribution does not move, so the electric dipole does not change direction. Hence, with time flowing forward, both dipoles point in the same direction, but with time reversed, the two point in opposite directions (figure 1c). This clearly violates time-reversal symmetry, and thus rules out a permanent EDM for the electron (or, indeed, any other stable particle) within the basic Standard Model.

However, as with any rule, there are exceptions to time-reversal symmetry. More sophisticated versions of the Standard Model do allow time-reversal violation, provided that there is also asymmetry in the behaviour of particles when their charges are reversed and “left” and “right” are exchanged. This is known as charge–parity (CP) symmetry violation. We know that CP violation must occur, because we have observed a pronounced asymmetry between matter and antimatter in the visible universe: for example, we observe far more electrons than positrons, so a world in which their charges were flipped would look quite different. Logically, therefore, time-reversal violation must also occur, and thus allow the electron to have a tiny permanent electric dipole moment.

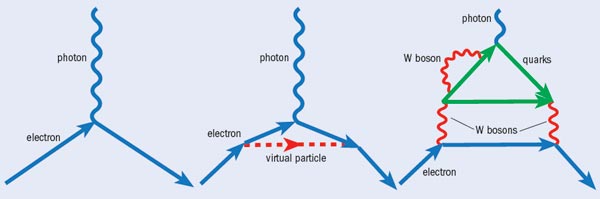
But how tiny is tiny? The size of the electron EDM can be calculated by considering the fleeting interaction between the electron and the “virtual particles” that appear from the vacuum energy of empty space and disappear before they can be measured directly (see “Feynman diagrams for an electron interacting with an electromagnetic field”). Some of these virtual-particle interactions violate time-reversal symmetry, and so the Standard Model predicts an EDM of at most 10^–39 e cm. This is far too small to be measured. However, most theories going beyond the Standard Model introduce new types of particles that violate time-reversal symmetry more easily. Such theories predict an electron EDM many orders of magnitude larger – 10^–25–10^–30 e cm. This is big enough that we can hope to detect it in precision measurements, and thereby start to rule out some classes of Standard Model extensions.

Searching for an EDM

If a non-zero electron EDM exists, how can we measure it? Again, it is useful to draw comparisons with the electron’s behaviour as a magnetic dipole. In quantum mechanics, the spin of the electron has two discrete states, “up” and “down”. As the energy of a dipole de_pends on its orientation with respect to the field, these two spin states have slightly different energies in a magnetic field: an electron with its spin aligned with the field has a slightly lower energy than one with its spin aligned opposite to the field. This energy difference leads to small changes in the energy levels of an electron in an atom, shifting the energy of some atomic states, and causing some single-energy states to split into two different states.

Similarly, when placed in an electric field, an electron with a small EDM will have a slightly lower energy when the dipole is aligned with the field than when the dipole is opposite to the field. For any plausible value of the electron EDM, however, the effect of the dipole interaction will be dwarfed by the interaction between the electron’s charge and the field. If we apply an electric field to a free electron, for example, the electron will simply rush off towards the positive pole.

The key to avoiding this problem is to look at electrons inside atoms or molecules. Such systems are electrically neutral and thus do not move in response to the electric field, but their energy levels still shift due to the EDM. In order to observe such a shift in the laboratory, the electron inside the atom must experience an electric field of more than 10⁶ V cm^–1. Such fields are not easily obtained, because when an electric field is applied to an atom, the electrons inside it respond by shifting their position relative to the nucleus, thereby cancelling out most of the field inside the atom. Relativistic effects keep the cancellation from being perfect, though, and in very heavy atoms, where the electrons move at speeds close to the speed of light, there can even be an enhancement of the applied field.

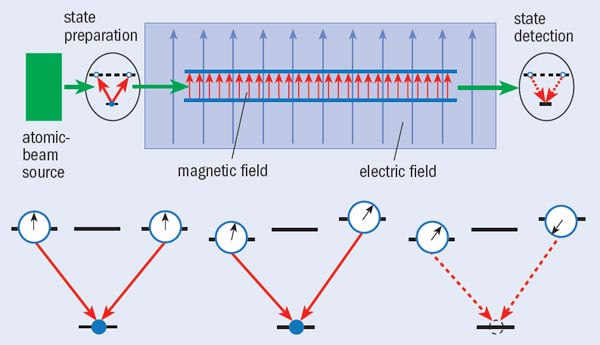
For this reason, the most accurate measurements of the electron EDM performed to date have used thallium atoms. Thallium, with an atomic mass of 205, has a field-enhancement factor of 585 – that is, the field experienced by the electrons inside thallium atoms is 585 times greater than the field applied in the lab. In a series of experiments in the early 2000s, researchers in Eugene Commins’ group at the University of California, Berkeley, first sent a beam of thallium atoms into a modest magnetic field. The presence of the field established a preferred axis for the electron spin, and thus the electron EDM (which must point along the same axis as the spin). They then applied an electric field of up to 1.23 × 10⁵ V cm^–1 along the same axis and looked for signs of a shift in the atomic energy levels that might be caused by an EDM.

To maximize their sensitivity to an EDM-generated shift, the Berkeley group used an interferometric technique similar to that used in atomic clocks, involving quantum-mechanical interference between two states of the same atom (see “Interferometric detection of an EDM shift”). The researchers looked for a shift in the interference pattern that depended on the applied electric field, and repeated the experiment with numerous combinations of electric and magnetic fields. Putting together 44 datasets, each consisting of measurements under 128 different conditions, they found that the electron EDM, if it exists, must be smaller than 1.6 × 10^–27 e cm.

From atoms to molecules

This result was enough to rule out one Standard Model extension (termed “naive supersymmetry” by a former member of the Berkeley group) that had predicted a larger EDM. But the Berkeley experiment pushed the limits of EDM searches in atoms. Three factors limited the measurement’s sensitivity: noise due to stray magnetic or electric fields; the interaction time of the atoms in the electric field; and the size of the energy shift due to the EDM.

On the first count, the Berkeley group went to extraordinary lengths to limit the effects of noise. The experiments were sensitive enough to pick up electrical noise caused by trains at a subway station almost a mile away. As a result, most of the researchers’ data had to be collected between 1 a.m. and 5 a.m., when the trains were not running. They also used parallel beams of sodium atoms as a “co-magnetometer” to rule out other sources of interference; the much lighter sodium atoms are not sensitive to an EDM, but would be sensitive to stray magnetic fields.

As for the other two limitations, the interaction time for the experiments was determined by the speed of the atomic beam, which was set by the 920 K operating temperature of their thallium source, and not easily changed. This left increasing the size of the EDM-related energy shift as the remaining hope for improving sensitivity. Doing so would require either significantly larger electric fields or a system with a larger field-enhancement factor. Unfortunately, applying a larger field presents significant technical challenges, and thallium is already close to the maximum enhancement factor – for atoms, at least.

A dramatic improvement in field-enhancement is possible, however, in molecular systems – in particular polar molecules consisting of one heavy element and one light one. The effective applied field in the Berkeley experiment, including the thallium enhancement factor, was about 72 × 10⁶ V cm^–1, but polar molecules can have fields of up to 20 × 10⁹ V cm^–1 – almost 300 times larger. Using molecules instead of atoms could, therefore, increase the sensitivity of EDM experiments by the same factor, to 10^–30 e cm or better. As a result, there has been a recent explosion of interest in polar molecules, with research groups beginning electron EDM searches at Imperial College London, and at Yale, Michigan, Oklahoma and Colorado universities in the US.

One of the current leaders in this effort is Edward Hinds’ group at Imperial, which uses ytterbium-fluoride molecules and a beam apparatus similar to that used in the Berkeley experiments. A beam of these molecules passes through a region containing a large electric field (13 kV cm^–1), and quantum state interference is used to search for the tiny shifts induced by an electron EDM. Their first measurement was published in 2002 and had a sensitivity of 0.2 × 10^–26 e cm, slightly worse than the Berkeley experiment. However, after a recent system upgrade, they expect to achieve a sensitivity of at least 5 × 10^–28 e cm by the end of 2009, and are hoping for another factor of three improvement by late 2010.

Another promising contender is David DeMille’s experiment at Yale University. The Yale group employs a different technique of holding lead-oxide molecules in a glass cell rather than sending them through the experimental apparatus in a beam. Although the cell needs to be maintained at about 973 K (a significant technical challenge), this technique means the researchers can keep the molecules interacting with the electric field for longer than is possible with beam experiments. The team expects to match or exceed the sensitivity of the Berkeley experiment in early 2010.

Meanwhile, other types of searches are also under way. A team led by Steve Lamoreaux at Yale and Larry Hunter at Amherst College is trying to detect an EDM in magnetic solids rather than diffuse molecular gases. Their approach is to use magnetic fields to align all the electron spins (and thus the EDMs) in a sample of solid gadolinium iron garnet and then measure the cumulative dipole moment of the whole sample. One advantage of this approach is that the density of electrons in a solid is much higher than in a gas, so the sensitivity to an EDM should also be higher than it is in the atomic and molecular experiments.

Assuming none of these experiments find a non-zero EDM, what happens after that? On the molecule front, the next major improvement will come from further increasing the time that the molecules spend interacting with the electric field. This can be done by performing the experiments using cold molecules, which move more slowly than room-temperature ones. David Weiss’ group at Pennsylvania State University is already using this approach in a new atom-based experiment where laser-cooled caesium atoms are trapped for up to a few minutes at a time, which leads to a projected sensitivity 200 times better than the Berkeley thallium experiment.

The Imperial and Yale groups are hoping for similar boosts as they begin work on cold-molecule experiments. The Imperial group plans to pre-cool its ytterbium–fluoride molecules by placing them in contact with helium vapour at 4 K before they enter the beam. The Yale group is also investigating a buffer-gas-cooled source, but the researchers and their collaborators at Harvard plan to switch to a new molecule, thorium monoxide, which offers a higher field-enhancement factor than lead oxide as well as the prospect of longer interaction times.

Tough times for theorists ahead?

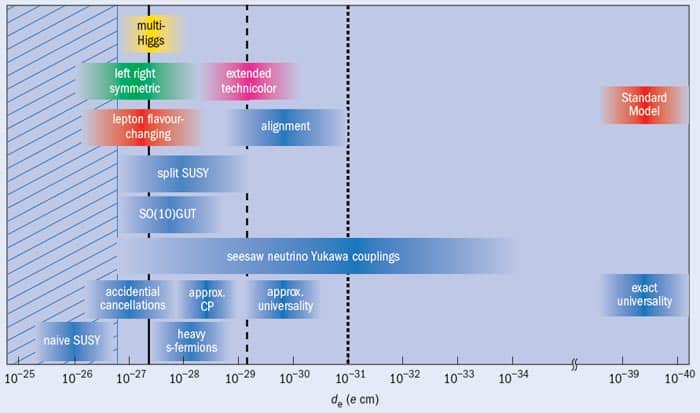
From a theoretical standpoint, there are a number of ways to reduce the predicted size of an electron EDM. Certain symmetry-violating effects can partially cancel it out, for example. Nevertheless, the vast majority of extensions to the Standard Model predict an EDM within a few orders of magnitude of the current experimental limit (figure 2). Hence, if any one of these models is correct, and if the cold-molecule experiments now in development reach their full potential, a non-zero EDM should be measured in the near future. Such a measurement would provide crucial information about symmetry violation in the universe, which would help explain why everything we see is made of matter rather than antimatter. On the other hand, if the proposed experiments do not find a non-zero electron EDM by the 10^–32 e cm level, life could become very difficult indeed for particle theorists. A null result would rule out nearly all existing theoretical approaches, and make it hard to explain the contents of the visible universe within our current theoretical framework.

For most theoretical scenarios, collider-based experiments and EDM searches are complementary. Colliders, for example, can create and detect new types of particles, which EDM searches cannot; on the other hand, the LHC cannot measure the symmetry-violating properties of particles. The two methods’ sensitivity is also similar: if there are new particles within reach of the LHC, there should also be an electron EDM within reach of the next generation of EDM searches. We will probably need a combination of both measurements to fully explain the universe we live in.

However, there is a chance that the symmetry violation due to new particles will be strong and not cancelled by other effects. If this is the case, and the EDM is smaller than about 10^–29 e cm, then any new particles would have larger masses than the LHC – or any other collider – could detect. In this case, EDM experiments will be our only hope of learning about physics beyond the Standard Model – all without even dissociating a molecule, let alone colliding protons.

At a Glance: The electron’s electric dipole moment

• The electric dipole moment d_e of two oppositely charged objects is equal to the magnitude of the charge, q, multiplied by the charge separation distance r, i.e. d_e = qr
• Under the basic Standard Model of particle physics, electrons cannot have a permanent electric dipole moment (EDM) because this would violate time-reversal symmetry, which states that physical interactions should look the same if time were to flow in reverse
• More sophisticated versions of the Standard Model theory do allow an electron EDM to exist, but they predict it would be far too small to measure in the lab. Hence, if experimentalists can find a non-zero EDM, this would indicate the existence of new physics beyond the Standard Model
• Several experimental groups are now searching for an EDM in atomic or molecular systems. Results from these precision measurements have already ruled out one proposed Standard Model extension, and a new generation of experiments with cold atoms or molecules should put others to the test

More about: The electron’s electric dipole moment

S Bickman et al. 2009 Preparation and detection of states with simultaneous spin alignment and selectable molecular orientation in PbO Phys. Rev. A 80 023418
J J Hudson et al. 2002 Measurement of the electron electric dipole moment using YbF molecules Phys. Rev. Lett. 89 023003
B C Regan et al. 2002 New limit on the electron electric dipole moment Phys. Rev. Lett. 88 071805
A C Vutha et al. 2009 Search for the electric dipole moment of the electron with thorium monoxide arXiV: 0908.2412v1