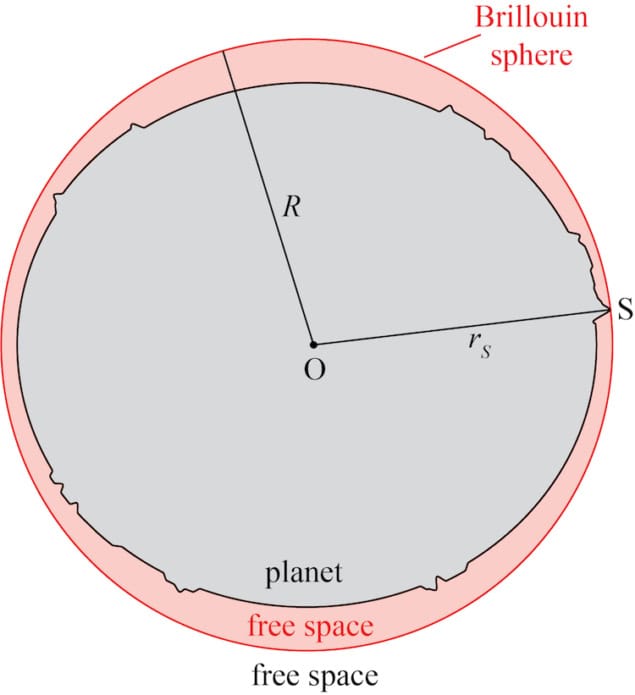
If the Earth was a perfect sphere or ellipsoid, modelling its gravitational field would be easy. But it isn’t, so geoscientists instead use an approximate model based on a so-called Brillouin sphere. This is the smallest geocentric sphere that the entire planet fits inside, and it touches the Earth at a single point: the summit of Mount Chimborazo in Ecuador, near the crest of the planet’s equatorial bulge.
For points outside this Brillouin sphere, traditional methods based on spherical harmonic (SH) expansions produce a good approximation of the real Earth’s gravitational field. But for points inside it – that is, for everywhere on or near the Earth’s surface below the peak of Mount Chimborazo – these same SH expansions generate erroneous predictions.
A team of physicists and mathematicians from the universities of Ohio State and Connecticut in the US has now probed the difference between the model’s predictions and the actual field. Led by Ohio State geophysicist Michael Bevis, the team showed that the SH expansion equations diverge below the Brillouin sphere, leading to errors. They also quantified the scale of these errors.
Divergence is a genuine problem
Bevis explains that the initial motivation for the study was to demonstrate through explicit examples that a mathematical theory proposed by Ohio State’s Ovidiu Costin and colleagues in 2022 was correct. This landmark paper was the first to show that SH expansions of the gravitational potential always diverge below the Brillouin sphere, but “at the time, many geodesists and geophysicists found the paper somewhat abstract”, Bevis observes. “We wanted to convince the physics community that divergence is a genuine problem, not just a formal mathematical result. We also wanted to show how this intrinsic divergence produces model prediction errors.”
In the new study, the researchers demonstrated that divergence-driven prediction error increases exponentially with depth beneath the Brillouin sphere. “Furthermore, at a given point in free space beneath the sphere, we found that prediction error decreases as truncation degree N increases towards its optimal value, Nopt,” explains Bevis. Beyond this point, however, “further increasing N will cause the predictions of the model to degrade [and] when N >> Nopt, prediction error will grow exponentially with increasing N.”
The most important practical consequence of the analysis, he tells Physics World, was that it meant they could quantify the effect of this mathematical result on the prediction accuracy of any gravitational model formed from a so-called truncated SH expansion – or SH polynomial – anywhere on or near the surface of the Earth.
Synthetic planetary models
The researchers obtained this result by taking a classic theory developed by Robert Werner of the University of Texas at Austin in 1994 and using it to write code that simulates the gravitational field created by a polyhedron of constant density. “This code uses arbitrary precision arithmetic,” explains Bevis, “so it can compute the gravitational potential V and gravitational acceleration g anywhere exterior to a synthetic planet composed of hundreds or thousands of faces with a triangular shape.
“The analysis is precise to many hundreds of significant digits, both above and below the Brillouin sphere, which allowed us to test and validate the asymptotic expression derived by Costin et al. for the upper limit on SH model prediction error beneath the Brillouin sphere.”
The new work, which is described in Reports on Progress in Physics, shows that traditional SH models of the gravitational field are fundamentally flawed when they are applied anywhere near the surface of the planet. This is because they are attempting to represent a definite physical quantity with a series that is actually locally diverging. “Our calculations emphasize the importance of finding a new approach to representing the external gravitational field beneath the Brillouin sphere,” says Bevis. “Such an approach will have to avoid directly evaluating SH polynomials.”

Physicists measure smallest gravitational field yet
Ultimately, generalizations of the new g simulator will help researchers formulate and validate the next generation of global gravity models, he adds. This has important implications for inertial navigation and perhaps even the astrophysics of exoplanets.
The team is now working to improve the accuracy of its gravity simulator so that it can better model planets with variable internal density and more complex topography. They are also examining analytical alternatives to using SH polynomials to model the gravitational field beneath the Brillouin sphere.
- The paper appears in IOP Publishing’s flagship journal, Reports on Progress in Physics, which now publishes original research.