As electromagnetic waves travel, they collect information about their environment. This property is widely exploited in a host of applications that rely on waves being deflected, scattered or reflected off their surroundings, but it comes with a challenge: how can we extract as much of this information as possible?
Researchers in Austria and France have now developed a new mathematical formalism that may help answer this question. The information the wave carries about its environment is known as Fisher information, and the new formalism makes it possible to visualize how waves collect this information from objects they interact with as they travel.
“The basic idea is quite simple: you send a wave at an object and the part of the wave that is scattered back from the object is measured by a detector,” explains theoretical physicist and study lead Stefan Rotter from TU Wien. “The data can then be used to learn something about the object – for example, its precise position, speed or size.”
Continuity effects
Rotter and colleagues found that a wave’s Fisher information matches a “continuity equation”, meaning that the information contained in the wave is preserved as it propagates, and obeys laws not dissimilar to the laws of energy conservation. This continuity equation allowed the researchers to calculate precisely where in the wave the information is actually located. They also discovered that different types of information on the properties of an object (such as its position, speed and size) are carried in different portions of the wave and that this information depends, with high precision, on how strongly the wave is affected by specific object properties.
“For example, if we want to measure whether an object is a little further to the left or a little further to the right, then the Fisher information is carried precisely by the part of the wave that comes into contact with the right and left edges of the object,” says TU Wien team member Jakob Hüpfl. “This information then spreads out, and the more of this information reaches the detector, the more precisely the position of the object can be read from it.”
Experimental tests in microwaves
The researchers tested their theory experimentally with help from collaborators in Ulrich Kuhl’s group at the University of Côte d’Azur in Nice. “We suggested that Felix Russo, a new masters student in our group, would be interested in carrying out the experimental part of the work and Kuhl agreed to host and supervise him,” says Rotter.

Metamaterial computer solves integral equations encoded in electromagnetic waves
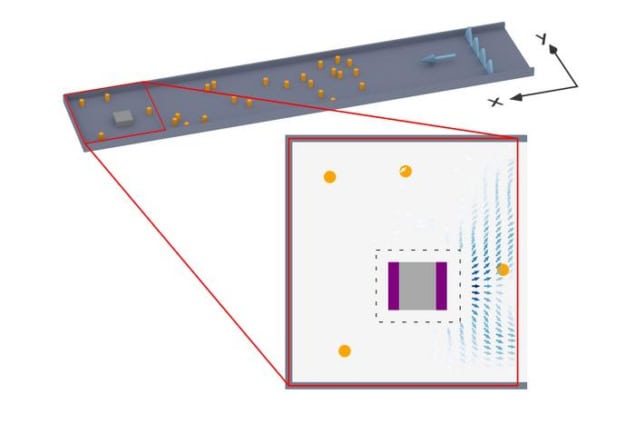
Russo began by sending microwaves through a structure made up of several randomly-positioned Teflon objects and a single metallic rectangle. The aim of the experiment was to determine the position of this rectangle by analysing data received at a detector on the other side of the structure.
“By precisely measuring the microwave field, it was possible to show exactly how the information about the horizontal and vertical position of the rectangle spreads: it emanates from the respective edges of the rectangle and then moves along with the wave – without any information being lost,” Russo says.
Applications in different fields
Rotter says the team’s formalism opens up a new way of thinking about how waves retrieve information from their environment. “Since this is such a widely used concept – ranging from seismology to biomedical imaging and from radar technology to quantum sensing – I expect our results to be useful in quite a broad range of different fields,” he tells Physics World.
The Vienna-Nice researchers are now working on extending their theory to multi-parameter sensing protocols and applying it to specific experimental settings. “Our goal is to demonstrate the advantages that can be gained in terms of designing an experiment and in improving the resulting measurement precision by using our technique,” Rotter says.
The present study is detailed in Nature Physics.



