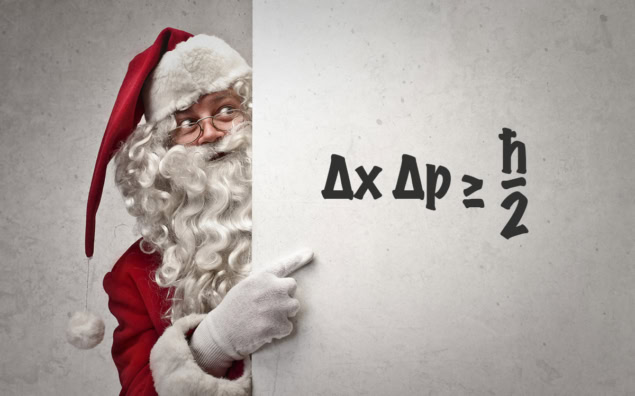
Each year, the International Association of Physics Students organizes a physics competition for bachelor’s and master’s students from across the world. Known as the Physics League Across Numerous Countries for Kick-ass Students (PLANCKS), it’s a three-day event where teams of three to four students compete to answer challenging physics questions.

In the UK and Ireland, teams compete in a preliminary competition to be sent to the final. Here are some fiendish questions from past PLANCKS UK and Ireland preliminaries and the 2024 final in Dublin, written by Anthony Quinlan and Sam Carr, for you to try this holiday season.

Question 1: 4D Sun

Imagine you have been transported to another universe with four spatial dimensions. What would the colour of the Sun be in this four-dimensional universe? You may assume that the surface temperature of the Sun is the same as in our universe and is approximately T = 6 × 10³ K. [10 marks]

Boltzmann constant, k_B = 1.38 × 10⁻²³ J K⁻¹

Speed of light, c = 3 × 10⁸ m s⁻¹

Question 2: Heavy stuff

In a parallel universe, two point masses, each of 1 kg, start at rest a distance of 1 m apart. The only force on them is their mutual gravitational attraction, F = –Gm₁m₂/r². If it takes 26 hours and 42 minutes for the two masses to meet in the middle, calculate the value of the gravitational constant G in this universe. [10 marks]

Question 3: Just like clockwork

Consider a pendulum clock that is accurate on the Earth’s surface. Figure 1 shows a simplified view of this mechanism.

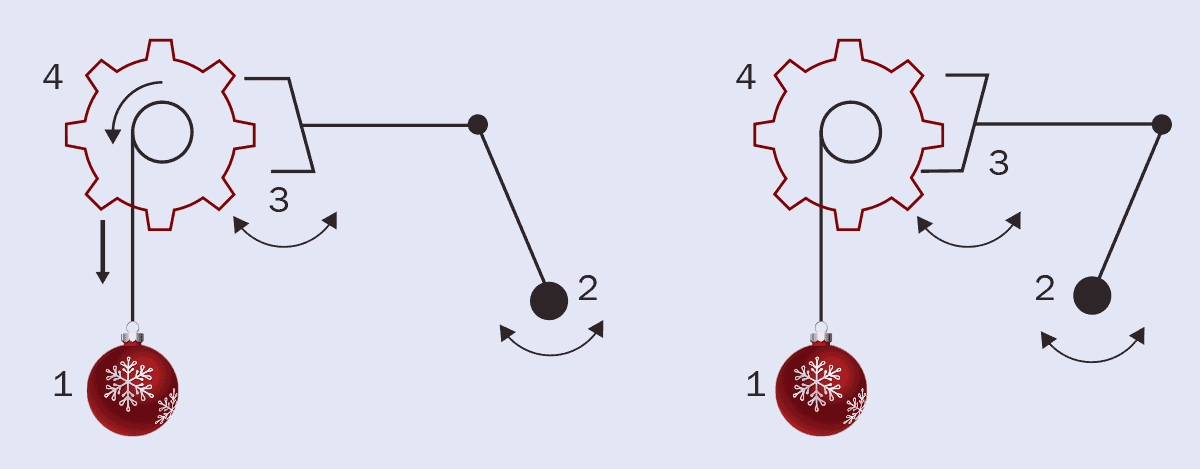
A pendulum clock runs on the gravitational potential energy from a hanging mass (1). The other components of the clock mechanism regulate the speed at which the mass falls so that it releases its gravitational potential energy over the course of a day. This is achieved using a swinging pendulum of length l (2), whose period is given by

$T=2\pi \sqrt{\frac{l}{g}}$

where g is the acceleration due to gravity.

Each time the pendulum swings, it rocks a mechanism called an “escapement” (3). When the escapement moves, the gear attached to the mass (4) is released. The mass falls freely until the pendulum swings back and the escapement catches the gear again. The motion of the falling mass transfers energy to the escapement, which gives a “kick” to the pendulum that keeps it moving throughout the day.

Radius of the Earth, R = 6.3781 × 10⁶ m

Period of one Earth day, τ₀ = 8.64 × 10⁴ s

How slow will the clock be over the course of a day if it is lifted to the hundredth floor of a skyscraper? Assume the height of each storey is 3 m. [4 marks]

Question 4: Quantum stick

Imagine an infinitely thin stick of length 1 m and mass 1 kg that is balanced on its end. Classically this is an unstable equilibrium, although the stick will stay there forever if it is perfectly balanced. However, in quantum mechanics there is no such thing as perfectly balanced due to the uncertainty principle – you cannot have the stick perfectly upright and not moving at the same time. One could argue that the quantum mechanical effects of the uncertainty principle on the system are overpowered by others, such as air molecules and photons hitting it or the thermal excitation of the stick. Therefore, to investigate we would need ideal conditions such as a dark vacuum, and cooling to a few milli­kelvins, so the stick is in its ground state.

Moment of inertia for a rod,

$I=\frac{1}{3}m{l}^2$

where m is the mass and l is the length.

Uncertainty principle,

$\Delta x\Delta p\ge \frac{\hslash }{2}$

There are several possible approximations and simplifications you could make in solving this problem, including:

sinθ ≈ θ for small θ

${\cosh }^{-1}x=ln \left(x+\sqrt{x^2-1}\right)$

and

${\sinh }^{-1}x=ln \left(x+\sqrt{x^2+1}\right)$

Calculate the maximum time it would take such a stick to fall over and hit the ground if it is placed in a state compatible with the uncertainty principle. Assume that you are on the Earth’s surface. [10 marks]

Hint: Consider the two possible initial conditions that arise from the uncertainty principle.

• Answers will be posted here on the Physics World website next month. There are no prizes.
• If you’re a student who wants to sign up for the 2025 edition of PLANCKS UK and Ireland, entries are now open at plancks.uk