The theory of quantum mechanics was born out of the need to explain how an object could behave both as a particle and as a wave. Since then, researchers have been attempting to understand and quantify the degree of “waveness” and “particleness” of quantum systems.
Now, Pawan Khatiwada and Xiaofeng Qian, both based at the Stevens Institute of Technology in the US, have published a paper in Physical Review Research unveiling the missing piece of the puzzle in the unique relationship between the wave and particle nature of a quantum object. The key piece is coherence, which describes the statistical phase relationship between the possible states a quantum system can adopt. If the phase relationship is well-defined, that is, stable and consistent, the system is coherent and therefore has the potential to exhibit interference, a wave-like property. If the system is incoherent, the phase relationship is random and variable. Coherence therefore characterizes the total capacity or potential of a quantum system to exhibit wave-like behaviour. The degree of waveness that is then realised and can be observed is known as the visibility and is characterized by the intensity of the maxima and minima in the interference pattern. The amount of particleness, known as the predictability, is a measure of how well we can predict the path a particle will take and is defined by the degree to which the particle is taking only one of the two paths.
The amount of interference that an object exhibits (the visibility) may only be a fraction of its total capacity to exhibit wave-like behaviour (its coherence) and can change according to how we choose to observe the system. For example, it we decide to track the position of the photon through a double-slit diffraction grating, no interference effects are observed, and the photon will behave as a particle. However, if we remove this tracking, the usual patterns of dark and light bands that are characteristic of interference emerge, and the photon behaves as a wave. In the first situation the visibility is low, but the coherence can nonetheless be high; it is our access to information about the path of the photon that destroys the interference pattern.
New quantum duality relation
Half a century ago, the relationship between a quantum object’s visibility and predictability was characterized by an inequality that restricted the sum of the square of the visibility and predictability to be less than or equal to one. However, this inequality could not have been telling the full story since it failed to capture the exclusivity of wave and particle-like behaviours such that if an object is more wave-like, it should display less particle properties and vice versa. The inequality instead permitted both wave and particle properties to increase or decrease simultaneously.
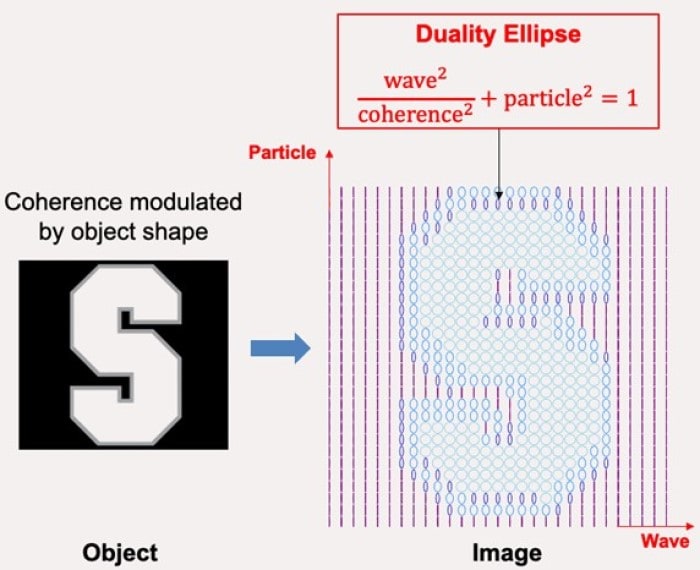
Qian and Khatiwada recast this inequality into a precise equality relation by introducing coherence as an additional variable. The relation then describes a trade-off between the coherence, visibility, and predictability, where the sum of the square of the predictability and the fraction of visibility exhibited out of the total coherence, must be equal to one. This relationship forms an ellipse equation, with the eccentricity determined by the coherence, where maximum coherence yields a circle and partial coherence an ellipse and is thus known as a duality ellipse relation.
Duality as a resource
Qian applies this formula to a technique for measuring quantum objects called quantum imaging with undetected photons (QIUP) first conceived by Nobel laureate Anton Zeilinger’s research group. One of a pair of entangled photons interacts with the object and depending on its shape, the coherence will change and can be tracked by following the behaviour of the second photon, without ever detecting the first. Information about the object is then given by the second photon even though it has never interacted with it. The more coherence is present at a specified location in the object, the more circular the duality ellipse relation (see figure).
Finding the eccentricity of the duality ellipse relation at each point in the object thus provides a map of its shape, and therefore an image of the object. Since the coherence is related to the visibility and predictability of a quantum object, Qian explains that their formula then becomes a crucial link between ‘fundamental properties of a quantum system like waveness and particleness and operational properties which hold information about an object’.

Physicists extend the wave nature of large objects
Of course, most experimental scenarios are not ideal, and Qian accounts for these experimental imperfections in a modified relation. Remarkably, the overall pattern of the elliptical duality relation remains the same and therefore this imaging technique proves to be robust even under such conditions.
Qian explains that ‘in a similar way quantum entanglement is a useful resource in quantum information and quantum computing, quantum duality also proves to be too for certain quantum tasks’. His group are now working on uncovering further avenues through which quantum duality can act as a quantum resource.