The techniques used to study various forms of soft condensed matter can be applied to living systems, but there are differences in the approaches of physicists and biologists, say Wilson Poon, Tom McLeish and Athene Donald

The links between physics and biology have become increasingly close in recent years. Many universities in the US have invested in interdisciplinary research institutes and the UK government has earmarked funding for the so-called life-sciences interface. At first sight, no area of physics seems more relevant to biology than soft condensed matter. After all, living things are made of complex fluids – liquids that contain mesoscopic structures with length scales of 1 µm and less – and physicists have long studied complex fluids such as colloids, polymers, liquid crystals and solutions containing soap-like molecules.
In fact, soft-condensed-matter physics has recently enjoyed a boom that has been fuelled, in part, by advances in synthetic chemistry. These developments have led to the kind of well characterized materials with which physicists like to work. Another important boost has come with the realization that many of the mathematical tools developed for other areas of theoretical physics can be used to describe soft matter. A third essential factor is the battery of new techniques that are available for the study of mesoscopic samples. These methods include a range of new microscopies, as well as scattering experiments at national and international facilities.
The study of complex fluids is now a coherent sub-discipline within condensed-matter physics. At the same time, the subject retains a distinctly interdisciplinary flavour and most research projects involve synthetic and physical chemists, materials scientists and chemical engineers, as well as physicists.
However, the dialogue between soft-condensed-matter physics and biology is not as well developed as one might expect. This is partly because soft matter is a relatively new sub-discipline of physics. There are also the usual barriers between diverse disciplines, such as different jargon and different journals. And the use of mathematics is a particular hurdle that physicists and biologists must overcome. But, in our opinion, there is also another obstacle that is specific to the dialogue between soft-condensed-matter physics and biology.
Different approaches
Modern biology functions under an essentially atomistic paradigm. The structure of many biological macromolecules can be determined to atomic resolution and can be related to the way that the molecule functions. If an atom located in the crevice of a protein moves by just a few angstroms (10-10 m), for example, the result could literally mean the difference between life and death. Details are all important in biology – ultimately, no protein is really like any other protein. Biology without atoms is, quite simply, inconceivable to the modern practitioner.
On the other hand, soft-condensed-matter physicists aim to find similarities between different types of complex fluids. In this “coarse-grained” approach, all polymers share certain common features – irrespective of the chemical details – because they are all long flexible chains. Such features can be understood by studying polyethylene, the simplest model system. The next level of complexity is to relate the topology of the chains to more general properties such as the viscosity of polymer solutions and melts.
It should now be obvious why the dialogue between those who study soft matter in general and those who study living soft matter may be fraught. Atoms turn biologists on, but turn physicists off. Biologists are rightly suspicious of physicists who tell them that one protein is just like any other because they are both “just polymers”. Perhaps that attitude is often an excuse for physicists who fail to learn enough biology before they offer their opinion. On the other hand, specialists in soft-condensed-matter physics can easily think that they have nothing to contribute after hearing an atomistic description of a typical biology problem.
This is an unfortunate situation because soft condensed matter does have things to contribute that are of genuine interest to biologists. In this article, we describe a number of problems where coarse-graining has provided a useful insight into biological soft matter. These areas include protein crystallization, the cell cortex, the build up of proteins responsible for “mad-cow” disease and Alzheimer’s disease, and cell adhesion in plants. This list is by no means exhaustive, but it illustrates a principle. We hope that these examples may act as catalysts to encourage dialogue between soft-condensed-matter physicists and biologists.
Protein crystallization
Although the first draft of the human genome was published earlier this year, scientists have still to overcome many major hurdles before they can harvest its riches. One such obstacle is the need to determine the structure of proteins. Our genes control the synthesis of the proteins that play a vital role in the structure and functioning of all forms of life. However, protein molecules only perform their biological function when they “fold up” to form particular 3-D structures. Knowledge of this 3-D structure therefore provides the most detailed starting point for understanding how proteins work.
Currently the favourite way to determine the structure of proteins is by X-ray crystallography (see Physics World May 1998 pp43-48). Protein crystals are usually formed by adding salts or polymers, such as polyethylene glycol, to induce crystallization in a protein solution. Surprisingly, the resulting crystals contain up to 50% water. Thus small molecules can diffuse more or less freely through a protein crystal, making it a novel template for catalysis applications.
The crystallization process is currently an art that is based almost entirely on practical know-how, rather than theoretical understanding. And progress is being hindered because new proteins are often only available in microgram quantities. The reason is either due to difficulties in synthesizing them, or because they only exist in small quantities in living tissues – as is the case for the proteins that build up in the brains of patients with CJD, the human form of mad-cow disease. Either way, trial and error is an expensive means of making protein crystals. Developments in “colloid physics” may be able to help.
A colloid is a homogenous material in which a second substance is finely dispersed. In solid-in-liquid colloids, the suspended solid particles interact via a potential, U(r), that depends on various properties of the solvent, including its dielectric constant and the presence of any dissolved species.
Colloidal particles undergo Brownian motion and can therefore reach thermal equilibrium. Thus, in many ways, a collection of colloidal particles is analogous to a simple atomic system, like argon. Indeed, the same theoretical and computational tools that were developed to understand the equilibrium phase behaviour and phase-transition kinetics of atomic systems can also be applied to understand colloids.
One of the simplest models of dense atomic systems is a collection of hard spheres. Indeed, an early result of computer simulations was that hard spheres should crystallize when the density is high enough – that is when the spheres occupy about half of the available volume. Peter Pusey of the University of Edinburgh and Bill van Megen of the Royal Melbourne Institute of Technology in Australia confirmed this behaviour in the early 1980s when they found that dense suspensions of nearly hard sphere-like plastic particles crystallized at the predicted density. Like their protein counterparts, colloidal crystals also contain a large amount of solvent.
More recently, experimentalists have found ways to vary the interparticle interaction in a colloidal suspension by adding an inert polymer that has a small radius of gyration, rg. The polymer can effectively add a short-range attractive force provided that rg – which is related to the molecule’s moment of inertia – is much smaller than the average radius, R, of the particles in the colloid. The technique works because the polymer molecules are excluded from a so-called depletion region between two particles that are separated by distances smaller than 2rg. Instead, the polymer molecules outside this region bombard the pair of colloidal particles to create a net force that pushes them together.
The equilibrium phase diagram of such a colloid-polymer mixture has been studied extensively in the last decade by groups at Edinburgh, the University of Utrecht in the Netherlands and elsewhere, using a combination of experiment, theory and simulation. The results have shown that polymers with rg << R enable dense colloidal crystals to form in solutions that are much more dilute than those that do not contain any polymer additives. The experiments have also provided insights into the kinetics of various phase transitions in such systems – insights that could hold the key to understanding protein crystallization.
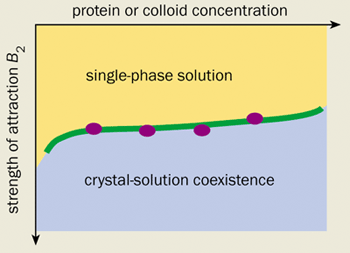
Indeed, there is now substantial evidence to suggest that the main role of the additives used in protein crystallization is to induce a short-range attraction between the protein molecules. For example, William Wilson’s group at Mississippi State University, and Chuck Zukoski and co-workers at the University of Illinois in the US have measured the strength of the attraction induced in a number of protein-additive solutions in light-scattering experiments. The results were surprising. They showed that dozens of so-called “globular” proteins begin to crystallize under identical conditions.
Even more surprisingly, one of the current authors (WP) has calculated that a synthetic colloid-polymer mixture exhibits almost exactly the same crystallization behaviour as globular protein solutions (see figure 1). This is an intriguing result. After all, the surface of a protein is extremely varied and water is a complicated liquid. We would therefore expect every protein to react differently to the addition of a salt or a polymer. We certainly would not expect to see anything universal about the phase diagrams of protein solutions, let alone be able to make comparisons with a model colloid-polymer mixture that has no directional or specific interactions.
Much remains to be learnt, of course, in particular about the complex pathways that lead to the nucleation and growth of crystals. Such insights are crucial for obtaining diffraction-quality crystals. But one thing is clear – further advances along these lines promise a quantitative toolkit for structural biologists who need to crystallize new proteins.
Physics and cells
All animal cells are enclosed by a thin membrane, which in turn covers a thin layer composed mainly of a protein called actin. This so-called cell cortex gives the cells their rigidity, while its deformation plays a crucial role in helping the cells to ingest food particles and crawl along surfaces.
Actin is a polymer of polymers. It is made up of many individual sub-units of a protein called G-actin. Under the right conditions, the G-actin can spontaneously polymerize to form semi-rigid filaments known as F-actin, which exists in high concentrations in the cell cortex (see figure 2). Biologists have known that the cortex is attached to the cell membrane by actin-binding proteins – molecules that bind to the F-actin filaments and insert themselves into the cell membrane.
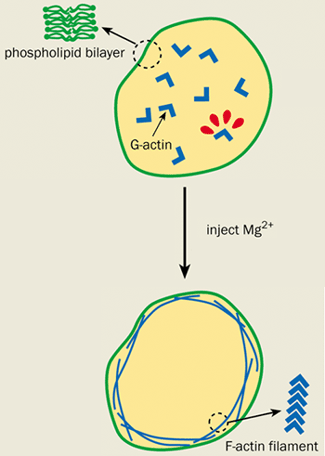
However, elegant physics experiments on artificial cells called giant vesicles have recently raised questions over the function of these binding proteins. Giant vesicles consist only of a membrane and are effectively empty cells. Eric Sackmann and co-workers at the Technical University of Munich in Germany were among the first to conduct experiments on them. His group recently enclosed a G-actin solution in an artificial cell and injected magnesium ions to initiate polymerization and form F-actin. The fate of the resultant actin filaments was monitored by attaching fluorescent molecules to the G-actin and studying them under a microscope.
Surprisingly, the F-actin formed a cortex just underneath the cell membrane even in the absence of actin-binding proteins. This cortex caused the vesicle to undergo the same shape changes that are observed in cells, but not in “bare” vesicles that do not have an actin layer.
Sackmann and colleagues built a simple physical model to explain this behaviour by treating the two basic components of the problem in the most coarse-grained way possible. They assumed that the vesicle membrane was a fluctuating elastic sheet and modelled the F-actin filaments as semi-flexible elastic rods. They found that the formation of a cell cortex is basically due to the desire of the rods to minimize elastic energy as they grow longer in a confined space.
Similar physics may operate in real cells. But if actin-binding proteins are not needed to attach the cortex to the cell membrane, then what role do they play? Sackmann and colleagues found some clues when they discovered that the presence of the artificial actin cortex hardly affects thermally driven elastic fluctuations in the vesicle. Perhaps it is the coupling of the cortex to the membrane by the actin-binding proteins that alters the mechanical properties of real cell membranes in ways that are not observed in model systems. Whatever the final answer is, it is clear that simple experiments performed under a coarse-grained soft-matter paradigm can shed light on important aspects of biological systems.
Protein folding gone wrong
When proteins are synthesized, they form long and flexible molecules that fold up to form a 3-D structure. However, the molecules need to fold into exactly the right structure in order to function properly. It is astonishing just how rarely misfolding occurs. Nature has devised a host of error-correcting mechanisms, most of which are barely understood. Yet one type of misfold arises again and again, causing a process known as amyloidosis, which is observed in a number of diseases.
Most proteins contain three types of discernible smaller “secondary structures” made up of many individual amino acids. Some sections of the protein coil into spring-like shapes known as “alpha-helices”, while others weave back-and-forth to form “beta-sheets”. The third type of secondary structure is random loops, which connect the helices and the sheets.
These sub-structures can perform vital functions. The alpha-helices, for example, form the “moving parts” of the protein that receive other interacting biomolecules, while the beta-sheets create barrel-shaped tunnels through cell membranes. But sometimes things go wrong and the beta-sheet structure can take over. In this case, the protein folds twist back and forth, first forming a long beta-sheet tape and then more complex, rigid fibrils as the individual tape-like proteins begin to self-assemble (see figure 3). Structures of this kind are known as amyloids, and appear in the brains of patients suffering from Parkinson’s disease and Alzheimer’s disease, and in tissue affected by some forms of cancer.

Amyloid structures are found in both proteins and in smaller protein-like units called peptides. When amyloids form in a solution they can have a dramatic physical effect. Small changes in temperature or pH, for example, can trigger the assembly of tape-like molecules in solutions containing less than 1% of peptide molecules. As a result, a low-viscosity solution rapidly turns into a stiff gel. To connect macroscopic regions of space with such little material – individual peptide polymers can measure up to a millimetre or more in length – is the everyday miracle of giant polymer molecules.
Biologists and chemists at the University of Leeds in the UK recently teamed up with experimental and theoretical physicists to investigate the process of amyloidosis in detail. Their studies have focused on a family of lightweight peptides that can self-assemble under carefully controlled and monitored conditions. The process can be switched on and off by changing the pH or the temperature, while the amyloid can be detected by a tell-tale feature in its ultraviolet spectrum.
The picture that emerges is of a delicate balance of specific atomic interactions and a more general structure that appears on a coarse-grained level. From a coarse-grained perspective, a peptide can be thought of as a small molecular rod. However, if specific hydrogen atoms are located along the rod so that the molecules can bond to each other, then the peptides can self-assemble to form long and flexible polymer tapes. This process of self-assembly is also governed by coarse-grained statistical mechanics. By knowing enough about the general requirements of self-assembly and solvent interactions, Amalia Aggeli and Sheena Radford designed a peptide from first principles that produced tapes in aqueous environments (see Aggeli in further reading).
Spectroscopy, microscopy and rheology have identified a whole hierarchy of self-assembled structures that depend only on the coarse-grained interactions of the tape-like objects. As the concentration of protein or peptide is increased further, the tapes first double-up and then stack into twisted fibrils. These fibrils then combine to form larger fibres (figure 3).
Astonishingly, the theorists in the Leeds team, Sasha Semenov and Irina Nrykova, find the same hierarchy in a very general statistical-mechanical model of self-assembling tape-like objects. In their model the complex local interactions of water-repelling and water-loving bonds can be summed into a small set of coarse-grained parameters.
One important insight that was gained from the calculations is the mechanism by which the stacking of tapes can be prevented from runaway growth. Theory shows that the natural twist of the tapes is progressively unwound as they stack up. Eventually the energy needed to twist another layer on the stack becomes greater than the attractive-energy gain, thus discouraging further additions to the stack.
The model may also explain the ease with which many natural proteins form amyloid fibrils. Moreover, extensions to this model predict that the timescales for molecular self-assembly can be very long and comparable to the gestation times for degenerative amyloid diseases. The old taunt “if it moves it’s biology, if it smells it’s chemistry and if it doesn’t work it’s physics” might be true in this sense. When the highly evolved structures and processes of biology take a wrong turn, the entropy-driven self-assembly of physics takes over.
What about plants?
Physics has opened a new window on botany. Indeed, the developments in microscopy, in particular, have been crucial to understanding the structure of plants on the mesoscopic length scale.
What, for example, controls how the cells in a plant stick together? As we have described, biochemists are likely to examine this question at the atomistic and molecular level. Recently, Keith Waldron and colleagues at the Institute of Food Research (IFR) in Norwich, UK, used fluorescence microscopy – among other techniques – to study the adhesion of plant cells. They identified ferulic acid as a key component in plants. The acid allows polymers to “cross-link”. In other words, it promotes the formation of side bonds between different chains in the polymer cell wall, which increases the adhesion between neighbouring components. Cross-linking thus provides good “sticking power” between the primary cell walls.
Work at the IFR has revealed why – as connoisseurs of Chinese food know – water chestnuts retain their crispness no matter how long they are boiled. Unlike most plants, water chestnuts contain significant levels of diferulic acid, which is bound in the cell walls and acts as a cross-linker.
Although fluorescence microscopy has made a big impact, it is wavelength limited and lacks the resolution of electron microscopy. Waldron and Andrew Smith, also at the IFR, have recently teamed up with one of us (AD) to address this issue. We have started exploring the capabilities of a so-called environmental scanning electron microscope (ESEM) to study the deformation in the cell walls of plants.

The images that are produced by an ESEM are essentially made up of low-energy electrons that are emitted by atoms at the surface, electrons that are back-scattered from atoms or molecules in the sample, and “environmental” electrons that are produced in ionizing collisions between any type of electron and water molecules in the ESEM chamber. Crucially, the presence of water vapour means that the hydrated state of the plant tissue can be maintained (see Donald in further reading).
Samples that are viewed with conventional electron microscopes usually have to be covered with gold beforehand. However, the ESEM allows hydrated samples to be imaged without coating. This means the water-based contents of fruit and vegetable cells can be studied in their natural state.
The relationship between the mechanical properties and the cellular structure of plants is of great economic interest in the food sector. However, plant tissue is increasingly being used to reinforce synthetic plastics and to manufacture biodegradable plastics. In either case, the tissue has to be handled appropriately. This might mean attempting to reduce juice losses due to cracking or breakage during harvesting. Conversely, in the juice- and oil-extraction industries, the tissues may be treated so that they break easily to release the cell contents.
New questions can now be addressed for the first time thanks to the ESEM. For example, we can now manipulate the adhesion between plant cell walls to obtain a better understanding of the process. To change the adhesion, we treated the epidermal layers of an onion with a chemical that can selectively attack components in the cell wall. We then observed how a crack advanced when the layers were placed under strain in a tensile testing rig – results that provided new information for modelling.
We found that the cell contents of fresh untreated onion cells remain intact until they rupture – at which point the contents “explode” into the microscope (figure 4a). In other words, the failure occurs within a single cell. However, we observed an entirely different failure mode after treating the onion with the chemical. In this case failure occurs between the cell walls (figure 4b).
Although the work is still at a very early stage, it reveals how advances in instrumentation are opening up new fields in the life sciences. We have shown that the deformation of tissue under natural or controlled living conditions that can be imaged directly with high resolution. Our work also stresses the point that physicists are exploring longer length scales than those studied by biochemists, who are usually more interested in the response of individual bonds rather than the whole cell.
Foams and fresh vegetables
Using the ESEM, we can also study how tissue behaves as we compress it. Lorna Gibson, now at the Massachusetts Institute of Technology, and Mike Ashby of Cambridge University made important progress in this area in the 1980s. They demonstrated that the compressive deformation of cellular solids, such as polyurethane foams, follows universal laws. These laws demonstrate simple power-law relationships between the bulk density of the foam and its mechanical properties, regardless of the chemistry of the foam. However, the laws are altered considerably if, like plant cells, the voids in the foam are full of fluid rather than air. Indeed, Mark Warner and Sam Edwards at the Cavendish Laboratory in the UK have recently shown that a fluid-filled foam is much stiffer than the corresponding unfilled foam. The reason is that the fluid is incompressible. However, universal laws can still be obtained.
How do fruit and vegetables behave when they are not fresh? In this case, the cell is only part full, and the cell walls are effectively slack. Warner’s recent theory predicts that the cell can be deformed rather easily at first. Then, once the cell has been squashed to the point where its volume is entirely filled, the cell should exhibit a stiffer response than can be described by the original theory.
Brad Thiel and one of us (AD) have directly tested these ideas in experiments on carrots. We left the vegetables to age for varying lengths of time to alter the degree of “turgor”, that is the amount of fluid that fills the cells. We found excellent agreement with Warner’s theory. His model, which was effectively tested on a particular type of filled foam (i.e. carrots), is another example of a coarse-grained model that enables physicists to draw general conclusions about a biologically complex structure.
If we want to manipulate and control the texture of fruit and vegetables by breeding and processing – or even by genetic modification if consumers agree – plant scientists must learn much more about the basic relationship between the architecture of the cell wall, its structure and its mechanical properties. Models will allow biologists to make predictions about plants. But models can only be developed if the correct mechanistic properties are understood by, for example, the direct visualization experiments we have described.
Rich pickings for physicists
Physicists like simple coarse-grained models but this can lead to our colleagues in multidisciplinary collaborations stereotyping us. Biologists and chemists expect physicists to come up with simplistic arguments based on “perfectly spherical cows”.
The point is, of course, that the adequacy of the “perfect sphere” model of a cow depends entirely on the problem under study. If all we want to know is how much more hide can be obtained by doubling the weight of a cow, then the spherical model can give a fairly accurate answer. But if we want to know what limits the size of four-legged animals, then it might be better to model the cow by two spheres that are connected by a rod – perhaps the strength of the animal’s neck is the limiting factor.
Similarly, whether a coarse-grained description that is rooted in soft-condensed-matter physics is adequate for understanding biomolecules depends very much on the problem being studied. We have found, for instance, that a model of a perfect sphere with a uniformly sticky surface is good enough to show the conditions under which protein crystals form. However, to understand other effects – such as the selection of crystal forms or the formation of gels – we probably need a slightly finer-grained model, such as a sphere with sticky patches. To build such a model, we need some input at the atomistic level. For example, we might need to know the typical distribution of water-repelling and water-loving chemical groups on the surfaces of proteins. And a certain amount of atomic-level information was needed to formulate the coarse-grained model of aggregating tapes and fibrils in amyloidosis.
As we see it, the challenge and fun lies in selecting just the right amount of atomistic detail to build coarse-grained models with maximal generality. In some sense, of course, that is precisely what physics is about. We are simply suggesting that biology offers rich pickings for soft-condensed-matter physicists who wish to apply their trade to new systems.



