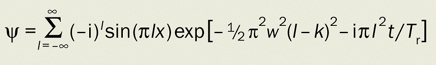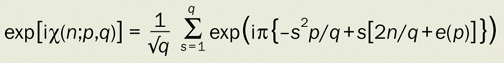In 1836 Henry Fox Talbot, an inventor of photography, published the results of some experiments in optics that he had previously demonstrated at a British Association meeting in Bristol. “It was very curious to observe that though the grating was greatly out of the focus of the lens…the appearance of the bands was perfectly distinct and well defined…the experiments are communicated in the hope that they may prove interesting to the cultivators of optical science.”

Talbot made his remarkable observation as he inspected a coarsely ruled diffraction grating, illuminated with white light, through a magnifying lens. With the lens held close to the grating, the rulings appeared in sharp focus, as expected. Moving the lens away, so that the grating was no longer in focus, the images should have become blurred but instead remained sharp. Moreover, the images consisted of alternating bands, the complementary colours (e.g. red and green) of which depended on the distance of the lens from the grating.

As the lens receded further, the sequence of colours repeated several times over a distance of the order of metres. With monochromatic light, the rulings of the grating first appeared blurred, as expected, but then mysteriously reappeared in sharp focus at multiples of a particular distance, z_T (figure 1).

Forgotten for decades

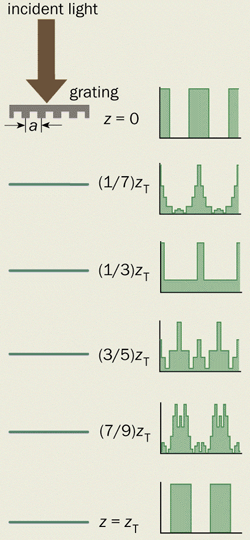
This “Talbot effect” – the repeated self-imaging of a diffraction grating – was forgotten for nearly half a century until it was rediscovered by Lord Rayleigh in 1881. Rayleigh showed that the so-called Talbot distance, z_T, is given by a²/L, where a is the slit spacing of the grating and L is the wavelength of the light. For red light with a wavelength of 632.8 nm and a grating with 50 slits per inch (a = 0.508 mm) the Talbot distance is 407.8 mm. Rayleigh pointed out that the Talbot effect could be employed practically to reproduce diffraction gratings of different sizes by exposing photographic film to a Talbot-reconstructed image of an original grating. Then the Talbot effect was forgotten again.

Recent investigations have revealed that the Talbot effect is far more than a mere optical curiosity. First, the effect is one of a class of phenomena involving the extreme coherent interference of waves. Second, these phenomena have deep and unexpected roots in classical number theory. And third, they illustrate something we are starting to appreciate more and more, namely the rich and intricate structure of limits in physics.

And who was Talbot? He is best known for his invention of photography, independently of French physicist Louis-Jacques-Mandé Daguerre, rather than the physics of diffraction gratings. And it is Talbot’s process, involving a negative from which many positive copies can be made, that we use in all non-digital photography today. But Talbot did much more: as an English landowner and parliamentarian, he ran the family estate at Lacock; he was one of the inventors of the polarizing microscope that has been indispensable to mineralogists; he proved theorems about elliptic integrals; and he contributed to the transcription of Syrian and Chaldean inscriptions.

Quantum revivals

There is a phenomenon in quantum physics that is closely related to the Talbot effect. A quantum wave packet – representing an electron in an atom, for example – can be constructed from a superposition of highly excited stationary states so that it is localized near a point on the electron’s classical orbit. If the packet is released, it starts to propagate around the orbit. This propagation is guaranteed by the correspondence principle: for highly excited states, quantum and classical physics must agree. The packet then spreads along the orbit, and eventually fills it. (It also spreads transversely – that is away from the orbit – but that is not important in this context.)

Over very long periods of time, however, something extraordinary happens: the wave packet contracts and after a time, T_r, returns from the dead and reconstructs its initial form. This is a quantum revival. As time goes on, the revivals repeat. In a wide class of circumstances, the reconstructions are almost perfect.

In the Talbot effect, the pattern of intensity is doubly periodic, both across the grating and as a function of distance from the grating. Similarly, for quantum revivals the probability density is both periodic around the nucleus and as a function of the time evolution of the wave packet. These periodicities are the result of coherent interference. Rayleigh understood this for gratings (where the interference is between the wavelets from the different slits), and there is a similar result for revivals. For a packet consisting of hydrogen-like states close to the nth energy level, E_n, the revival time is of the order of nT_c, where T_c = hn³/2E₁ is the orbital period of a classical electron and h is Planck’s constant. Because of these periodicities, the intensities can be depicted as repeating patterns in the plane that resemble exotic carpets or alien landscapes (figures 2 and 3).

Now comes the number theory. In addition to the reconstructed Talbot images at z = z_T and quantum revivals at t = T_r, there are more complicated reconstructions at fractional multiples of the Talbot distance and the revival time. The Talbot image at distance (p/q)z_T is a superposition of q copies of the initial grating separated by a/q (figure 1). Thus if p/q = 3/5, there are five superposed images. This is the fractional Talbot effect. And the quantum wave at time (p/q)T_r is a superposition of q copies of the initial wave packet, separated by an angular distance 2 pi/q. These are the fractional revivals.

At the heart of the rather complicated mathematical explanation of this remarkable phenomenon is the simple identity (-1)ⁿ² = (-1)ⁿ, where n is an integer that labels the contributing wavelets. The application of this identity greatly simplifies the sums over the contributing wavelets. Each image in a reconstruction has the same amplitude, 1/q^1/2, and its phase is given by beautiful sums discovered by Gauss at the end of the 18th century (see box). In words, the phase of the nth image is the direction of the resultant vector when q unit vectors are added in the complex plane. The angle between the first pair of vectors is 2 pi n/q (plus a constant that does not depend on n) and decreases by 2 pi p/q for each successive pair. The rich patterns of the carpets originate in the complicated patterns of the phases of the Gauss sums (figure 4).

On closer inspection, diagonal “canals” can be seen criss-crossing the carpets. In Talbot carpets, the canals are minima of intensity that are correlated between neighbouring image planes. In quantum carpets, they are space-time structures corresponding to features of the wave that move at fixed velocities (unrelated to the speed of the classical packet). The canals can be understood in several equivalent ways: in terms of destructive interference between positive- and negative-order diffracted beams (that is Fourier components of the patterns); by the transverse structures that remain after averaging along the anticipated directions of the canals; and by arguments involving position and momentum simultaneously (through the evolution of Wigner functions in phase space).

Fractal carpets

Both Talbot and quantum carpets can have intricate fine structure. Consider the case where the transparency of the grating is discontinuous, as it is in the Ronchi grating where the rulings consist of sharp opaque and transparent bars. Alternatively imagine that the quantum wave is discontinuous, as for a particle in a box where the initial wave amplitude plummets to zero at the walls, even though it varies smoothly inside the box.

In Talbot terminology the reconstructed images in the plane z = (p/q)z_T consist of q superposed copies of the grating, complete with discontinuities. Although there is an infinite number of images at fractional distances, they still represent an infinitesimal subset of all possible images.

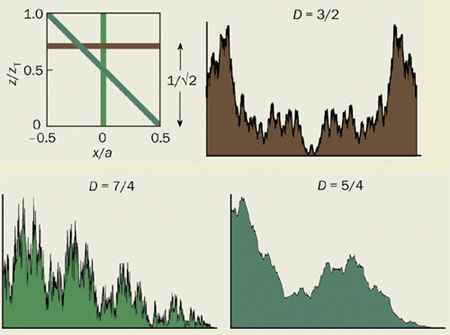
What happens in planes that are irrational fractions of the Talbot distance, for example z_T/2^1/2? The light intensity is then a fractal function of distance x across the image. To be precise, this means that the graph of intensity as a function of x, regarded as a curve in the plane, is continuous but not differentiable. In other words, although the intensity has a definite value at every point, the curve has no definite slope and so is infinitely jagged. Such curves are described as having a “fractal dimension”, D, between one (corresponding to a smooth curve) and two (corresponding to a curve so irregular that it occupies a finite area). Carpets generated by Ronchi gratings, for example, have a fractal dimension of 3/2 (figure 5).

Carpets are functions of the longitudinal coordinate z (along the propagation direction) as well as the transverse coordinate x, so the wave intensities can be plotted as surfaces on the x–z plane (see figure 3b, for example).

What is the fractal dimension of these Talbot or quantum landscapes? As these landscapes are surfaces, they have a dimension that takes a value between two and three. For a surface where all directions are equivalent, the dimension of the surface is one greater than the dimension, D, of a curve that cuts through it. For a Talbot landscape, where the fractal image curves have D = 3/2, we might expect the dimension to be 1 + 3/2 = 5/2.

But Talbot landscapes are not isotropic. For fixed x, the intensity also varies as a function of distance z from the grating, with a fractal dimension of 7/4 (figure 5). Therefore the longitudinal fractals are more irregular than the transverse ones. Finally, the intensity is more regular along the diagonal canals because of the cancellation of large Fourier components and has fractal dimension of 5/4 (figure 5). The landscape is dominated by the largest of these fractal dimensions, and so is a surface with dimension 1 + 7/4 = 11/4.

This fractal structure also applies to the evolving wave from a particle in a box with uniform initial wave amplitude. There are space fractals (varying x with constant t), where the graph of the probability density has D = 3/2; time fractals (varying t with constant x), where the graph of the probability density has D = 7/4; and space-time fractals (along the diagonal canals), where D = 5/4. Some of these results about fractals can be generalized to waves evolving in enclosures of any dimensions, even with shapes that do not give rise to revivals, provided the initial state is discontinuous, even if only at the boundary.

Asymptotic physics

There is, however, a sense in which the carpets – at least as we have described them – are fictions. Like all calculations in physics, they rely on approximations that are valid only in certain limiting circumstances. For a start, the perfect Talbot reconstructions, and the ideal fractals in the case of gratings with sharp-edged slits, depend on the illuminating wave being perfectly plane and infinite in extent.

Obviously this is not true in practice, and corrections can be calculated. For N illuminated slits, the finest details of the reconstructed images and of the fractals are blurred transversely by Delta x ~ a/N and longitudinally (i.e. in the depth of focus of Talbot images) by Delta z ~ z_T/N².

More fundamental is the fact that the finite wavelength of the light, L, must limit the fine detail in the optical field, so that even with infinitely many slits the images would still be blurred.

Perfect reconstruction is an artefact of the paraxial approximation, in which the deflections theta of all relevant diffracted beams are assumed to be small, so that cos theta ~ 1 – theta²/2. Deviations from this approximation get smaller as the ratio L/a decreases, that is in the short-wave limit, or for coarse gratings. The blurring in both the transverse and longitudinal directions is of the order of (aL)^1/2. However, the blurring in z is much smaller relative to the periodicity in the pattern because the detail is stretched over the Talbot distance, which greatly exceeds the slit spacing.

These blurrings should not be confused with the more familiar Fresnel diffraction of light from a single edge of a slit, which would be of order a in the transverse direction at z = z_T. An alternative way to state the Talbot effect is that the Fresnel blurring from the edges of all the slits is cancelled by the coherent interference of the waves.

In the quantum case, the perfection of the revivals is degraded by an effect that seems different but is mathematically very similar. Analogous to the paraxial approximation is the assumption that the energy can be approximated by terms that are both linear and quadratic functions of the quantum number n, over the range of energies included in the initial state. (If the variation were merely linear, then the wave packet would not spread at all.)

In the case of a non-relativistic particle in a box, the revivals are perfect because the variation in energy is quadratic. However, quadratic variation only approximately describes an electron in an atom: the approximation is semi-classical, that is it gets better as the quantum number, n, corresponding to the central energies in the packet increases. Non-quadratic corrections to the spectrum degrade the revivals, in ways that are now well understood.

Paradoxical limits

Quantum and optical carpets provide a dramatic illustration of how limits in physics that seem familiar can in fact be complicated and subtle. It is no exaggeration to say that perfect Talbot images, and infinite detail in the Talbot fractals, are emergent phenomena: they emerge in the paraxial limit as L/a approaches zero.

At first this seems paradoxical, because the short-wave approximation is usually regarded as one in which interference can be neglected, whereas the Talbot effect depends entirely on interference. The paradox is dissolved by noting that the Talbot distance increases as the wavelength approaches zero, so here we are dealing with the combined limit of short wavelength and long propagation distance: in the short-wavelength limit, the Talbot reconstructed images recede to infinity.

In a similar way, perfect quantum revivals emerge from the semi-classical limit of highly excited states. Again it might seem paradoxical that an interference effect persists in a semi-classical limit (and indeed emerges perfectly in that limit). The dissolution of the paradox is analogous to that in the Talbot case: the semi-classical limit here is combined with the long time limit (recall that T_r ~ nT_c), so the revivals occur in the infinite future.

Even within the paraxial approximation, a clash of limits can generate very rich phenomena. Consider a transparent phase grating, that is a diffraction grating that transmits light with uniform amplitude but introduces a sinusoidal phase variation with period a.

In the geometrical-optics approximation, light rays passing through the grating are deflected so that they are normal to the sinusoidal wavefront that is generated immediately beyond the grating. These rays generate the pattern shown in figure 6a, which is dominated by caustics, i.e. curves onto which the light is focused and in which the intensity is concentrated.

Pairs of caustics join at cusps located near the centres of curvature of the wavefronts. The resulting pattern of rays is not periodic in z, and is thus discordant with the notion that the pattern of waves must repeat with period z_T for the Talbot effect to occur. Again the paradox is dissolved by the observation that the Talbot distance is of the order of 1/L, and so recedes to infinity in the geometrical-optics limit where L tends to zero.

However, when L/a is small but non-zero, both the caustics and the Talbot repetitions must coexist. This means that the geometrical caustics, including the cusps for distances much less than the Talbot distance, must be regenerated at both integer multiples and fractional multiples of z_T. Figures 6b and c show the Talbot carpet for this sinusoidal grating, with apparently no trace of the geometrical-optics caustics and their cusps.

However, appropriate magnification shows that the original and regenerated caustics (and associated diffraction fringes associated with a single sinusoid) are indeed hidden in the detail of the carpet (figures 6d and e). It is worth emphasizing what a remarkable phenomenon this regeneration is: geometrical-optics caustics have been constructed entirely by interference, in regions where there are no focusing rays. They are the ghosts of caustics. There is a curious analogy between these “caustics without rays” and Moiré patterns, which are “fringes without waves”.

Experiments and outlook

These predictions – Gauss sums, waves reconstructing themselves, fractal carpets and canals – are not just arcana from the imaginations of theorists. Many of the results have been confirmed by experiments.

Fractal aspects of Talbot interference were seen in optical experiments by one of us (MB) and Susanne Klein of Bristol University in 1996. Fractional Talbot images were seen in matter waves (a beam of helium atoms) diffracted by a microfabricated grating, in experiments carried out at the University of Konstanz in 1997 by Stephan Nowak, Christian Kurtsiefer, Christian David and Tilman Pfau.

And fractional quantum revivals have been seen in electrons in potassium atoms, which were knocked into appropriate initial states by laser pulses using a “pump-probe” technique. These experiments were performed by John Yeazell and Carlos Stroud at the University of Rochester in 1991. Analogous observations of the vibrational quantum states of bromine molecules were carried out in 1996 by Max Vrakking, David Villeneuve and Albert Stolow at the University of Ottawa in Canada.

There are also the beginnings of applications for technology. Following Rayleigh’s pioneering example, the fine detail in Talbot wavefunctions is being employed in lithography. And the number-theory properties of the phases have been proposed as the basis of a means to carry out arithmetic computations based on interference.

However, the predicted Talbot reconstruction of caustics for smooth phase gratings has yet to be observed. An appropriate grating for such experiments could be a sheet of glass with an undulating surface, or a wave on water. And as the manipulation of electronic and molecular wave packets with ultra-short laser pulses gets more sophisticated, we envisage more detailed experimental exploration of the fine structure of the carpets, such as the diagonal canals.

The optical field behind a coherently illuminated diffraction grating, and the quantum particle in a box with uniform initial state, are two of the most venerable and widely studied systems in physics. It was quite unexpected to discover such richness hidden in them, and also to see it displayed by such a wide range of physical systems. Further exploration of these intricate manifestations of the coherent addition of waves is a fitting way to celebrate the bicentenary of Thomas Young’s great discovery of the interference of waves of light.