When water vapour spontaneously condenses inside capillaries just 1 nm across, it behaves according to the 150-year-old Kelvin equation – defying predictions that this pre-quantum-era formula would inevitably break down at the atomic scale. This is the finding of researchers at the University of Manchester, who showed that the equation remains valid even for capillaries that can accommodate only a single layer of water molecules.
Condensation inside capillaries is ubiquitous in nature, and many physical processes – including friction, stiction, lubrication and corrosion – are affected by it. The Kelvin equation, which relates the surface tension of water to its temperature and the diameter of its meniscus (among other parameters), predicts that if the ambient humidity is between 30–50%, then flat capillaries less than 1.5 nm high will spontaneously fill with water vapour that condenses from the air.
In the real world, though, capillaries can be even smaller than this. At this scale, it becomes impossible to define the curvature of a liquid’s meniscus – meaning that the Kelvin equation should no longer hold. However, because such tight confinement is difficult to recreate in the laboratory, researchers have been unable to test this hypothesis until now.
Smallest capillary possible
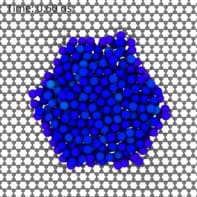
The Manchester team led by Andre Geim and Qian Yang created their ultra-tiny capillaries by meticulously sandwiching strips of graphene (a two-dimensional sheet of carbon) between atomically flat crystals of mica or graphite using a process called van der Waals assembly. The graphene strips act as spacers and their thickness can be varied, allowing for capillaries of varying heights. Some are just one atom high, which Geim explains is the smallest capillary possible, allowing only a single layer of water molecules to pass through.
Using atomic force microscopy (AFM), Geim, Yang and colleagues imaged the capillaries as they filled with water. These data showed that capillary condensation follows the Kelvin equation even in these tiny structures. “The result came as big surprise,” Yang says. “We expected a complete breakdown of the equation since the properties of water change at this scale, with its structure becoming distinctly discrete and layered.”
Why no breakdown?
At the atomic scale, Yang explains that researchers rewrite the Kelvin equation in terms of how water molecules in both gas and liquid phases interact with solid surfaces (such as capillary walls). In this form, macroscopic quantities such as the contact angle of water with the capillary wall, the surface tension of water and its meniscus curvature all disappear from the equation, which then remains valid as long as the energy of the water-surface interactions does not notably change.
Frictionless flow in 2D channels
“In practice, however, the condition breaks at about four to five layers of confined water (which are less than 2 nm thick in total),” she tells Physics World. “Under stronger confinement still, the water structure strongly changes, and the interaction energies (primarily the liquid water-surface energy) inevitably change.” In this regime, the Kelvin equation should obviously fail — mainly because huge oscillations in the relative humidity at which condensation occurs are expected due to the aforementioned layered structure of water.
What the Manchester team found, though, is that these oscillations are strongly suppressed by the elasticity of the capillary walls. Although these walls adjust their position by less than 0.1 nm in response to the high pressures (of up to 1000 bars) present during capillary condensation under ambient humidity, Yang says that this miniscule adjustment is enough to snugly accommodate only an integer number of water-molecule layers. As a result, she concludes, “the Kelvin equation remains valid down to a monolayer of confined water”.
Full details of the research are described in Nature.