The long-standing problem of the cosmological constant, described both as “the worst prediction in the history of physics” and by Einstein as his “biggest blunder”, is being tackled with renewed vigour by today’s cosmologists. Rob Lea investigates
The cosmological constant has been a thorn in the side of physicists for decades. Even though its purpose in modern cosmology differs from its original role, the constant – commonly represented by Λ – still presents a challenge for models designed to explain the expansion of the universe.
Simply put, Λ describes the energy density of empty space. One of the main issues stems from the fact that Λ’s theoretical value, obtained through quantum field theory (QFT), is nowhere near the value obtained from the study of type Ia supernovae and the cosmic microwave background radiation (CMB) – in fact it diverges by as much as 10121. It is therefore of little wonder that cosmologists are eager to tackle this disparity.

“The cosmological constant problem, in one form or another, is a century-old puzzle. It is one of the biggest problems in modern physics,” says theoretical physicist Lucas Lombriser from the University of Geneva (UNIGE), Switzerland. “Moreover, the cosmological constant is the most dominant component in our universe. It makes up 70% of the current energy budget. How could one not want to figure out what it really is?”
Indeed, with a new generation of cosmologists now on the scene, there are some rather radical ideas and revisions of older theories. But can the field accept these revolutionary ideas, or has Λ become a comfortably familiar burden?
Still crazy after all these years
The cosmological constant was first introduced to models of the universe by Albert Einstein in 1917. To the physicist’s own surprise, his general theory of relativity (GR) seemed to suggest that the universe is contracting, thanks to the effects of gravity. The consensus at the time was that the universe is static and, despite having already revolutionized several long-held ideas, Einstein was unwilling to challenge this particular paradigm. This desire to preserve the stability of the universe led Einstein to make an addition to GR’s equations. Later, he would infamously describe this as his “biggest blunder”.
“When Einstein was applying GR to cosmology, he realized he could add a constant to his equations and they would still be valid,” explains Peter Garnavich, a cosmologist at the University of Notre Dame, France. “This ‘cosmological constant’ could be viewed in two equivalent ways: as a curvature of space–time that was just a natural aspect of the universe; or as a fixed energy density throughout the universe.”
Thus, the initial role of Λ was to counterbalance the effects of gravity and help ensure a steady-state universe that is neither expanding nor contracting. This role, however, became obsolete following Edwin Hubble’s discovery in 1929 that the universe is expanding. When Einstein was finally convinced of this, Λ was designated to the cosmic dustbin. Yet, like the proverbial bad penny, it would resurface in a different form decades later.
Whereas once the cosmological constant was used to balance the universe against expansion, in modern cosmology Λ represents vacuum energy – the inherent energy density of empty space – that no longer just balances gravity , but overwhelms it. That doesn’t mean Λ has become any less problematic, though. “In 1998 the High-Z Supernova Search team discovered that the expansion rate was accelerating instead of decelerating,” says Garnavich, who took part in the research using type Ia supernovae to study the expansion of the universe. This requires some form of additional energy throughout the universe or some more exotic explanation. This driving force is referred to as “dark energy”, and the term itself has become a placeholder for the various theoretical entities that could account for this accelerating expansion. Suspects range from vacuum energy, the current most favoured model; to quantum fields; and even fields of time-travelling tachyons – hypothetical particles that travel at faster-than-light speeds.
The cosmological constant serves as the simplest possible explanation for the dark energy that drives this accelerating expansion, and its theoretical value should therefore match observations. Unfortunately, as mentioned, the former is greater than the latter by some 120 orders of magnitude. Clearly, Λ’s reputation as “the worst prediction in the history of physics” isn’t mere hyperbole.
Getting a head start on the problem
The role of dark energy in the early universe has been on the mind of Luz Ángela García, a physicist and astronomer at Universidad ECCI, Bogotá, Colombia. Together with her collaborators Leonardo Castañeda and Juan Manuel Tejeiro from Observatorio Astronómico Nacional, Universidad Nacional de Colombia, García is putting forward an “early dark energy” (EDE) model as a potential solution to the cosmological constant problem (New Astronomy 84 101503).
The radical element about the team’s proposal is the idea that cosmological models might not need the cosmological constant at all. Of course, there is still that accelerating expansion to consider, so to account for this, García looks to other sources. “When I first approached this field, I came across the inconsistency with the values predicted from both cosmology and high-energy physics, and tried to formulate an alternative model to Λ by studying possible candidates to explain the accelerated expansion of the universe,” she says.
Λ, as it is currently considered, only accounts for the universe’s expansion once matter began to form structure – an era that lasted from 47,000 years to 9.8 billion years after the Big Bang. García wanted to consider a form of dark energy that began to play a role in the earlier, “radiation-dominated” epoch, from the earliest moments of “cosmic inflation”. Inflation – the sudden and very rapid expansion of the early universe – is thought to have taken place some 10−36 seconds after the Big Bang, but this rapid expansion is thought to have been driven by quantum fluctuations, and not dark energy. Eventually, the attractive force of gravity slowed this expansion, until about 9.8 billion years into the universe’s history, when dark energy began accelerating its expansion once again (figure 1). García and colleagues, however, describe this dark energy as an entity that could have been present in both the radiation-dominated and matter-dominated epochs as a “non-interacting perfect fluid” that evolved with the universe’s other components.
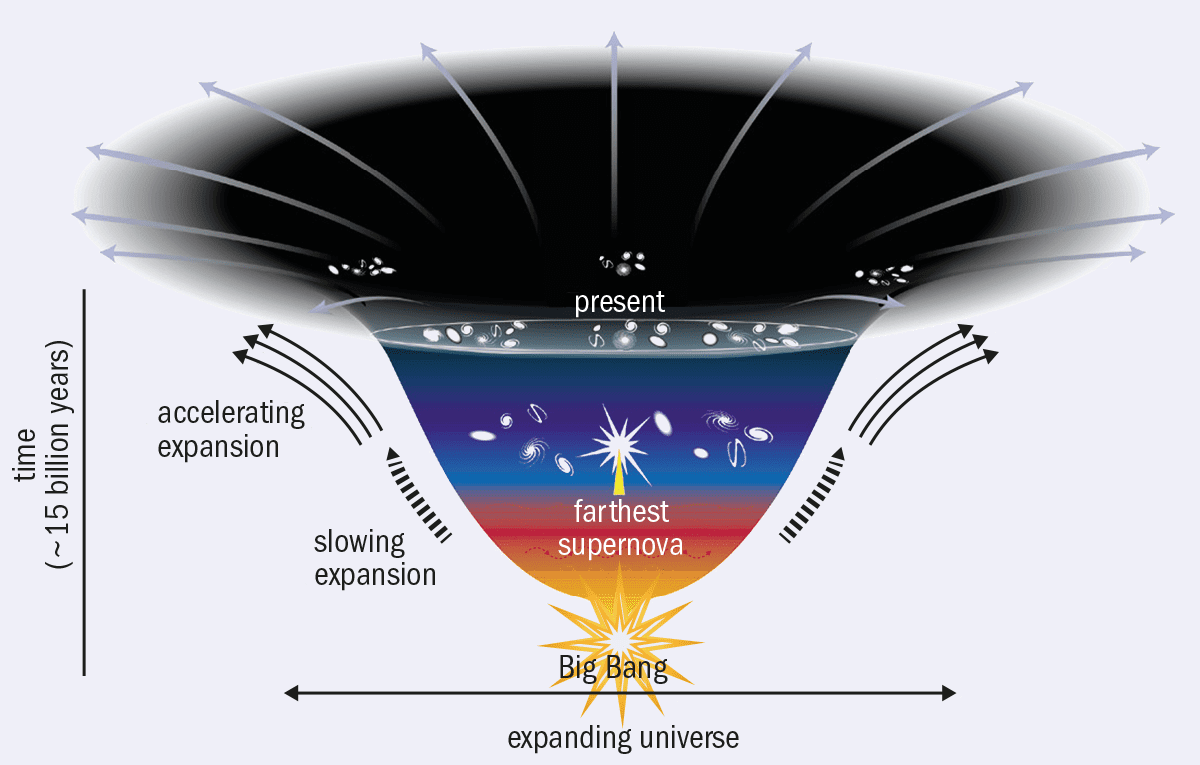
“The model’s strengths are the following: first, it provides a compelling description of the universe’s accelerated expansion during its current epoch, beginning around four billion years ago,” García explains. “Second, our formulation allows for evolution with redshift instead of the cosmological constant, in which energy density does not change over time.” This could explain why the theoretical value suggested by QFT is larger than the value given by the redshifts of distant supernovae. The value has evolved over time.
García identifies a further strength of her EDE model, which is that it offers several predictions that match up well with practical measurements and high-resolution data concerning various stages of the universe’s evolution. The result is a theoretical picture that matches the ratio we observe in the current dark-energy-dominated epoch of our universe, where its matter/energy content is dominated by the accelerating force. “Of course, we could use both the cosmological constant and our EDE, but it makes the description unnecessarily complicated, and there is not a physical justification for that,” says García. “We only need one component to describe the accelerated expansion of the universe today.”
If the decision to eliminate the cosmological constant, or set it to zero, taken by García and her collaborators seems somewhat arbitrary, she points out that there is almost an “arbitrariness” inherent to the introduction of the constant in the first place. “There is no fundamental reason to take for granted that dark energy has to manifest as the cosmological constant,” she remarks. “We have not detected any form of dark energy nor the cosmological constant; therefore, any form of dark energy is valid until the data confirm or refute its existence.”
The EDE that García suggests isn’t perfect. Indeed, it comes with elements that the wider scientific community may be reluctant to adopt. But she doesn’t shy away from pointing out the potential flaws in her own ideas. “There are two issues that the community could find troubling,”García admits. “On the one hand, more complex models imply a broader set of free parameters. It is not something we desire for our formulations, because those parameters might not have a direct physical interpretation. In that sense, the cosmological constant is an advantageous model, because it has a minimal number of free parameters, all of them constrained with current observations.”
We have been revising and looking for more sets of observational data to validate our models. Hence, we are creating a bridge between theory and observational cosmology
The second thing that García admits may cause some caution is that the model has yet to be submitted to many observational probes. “We have been revising and looking for more sets of observational data to validate our models. Hence, we are creating a bridge between theory and observational cosmology.”
The “well-tempered” cosmological constant
Forcing the cosmological constant to take a value of zero may lead the curious cosmologist to consider what happens if we do the opposite. In other words, what would happen if we allow it to take an arbitrarily large value, similar to the value purported by QFT.
Stephen Appleby, a cosmologist at the Asia Pacific Center for Theoretical Physics in Pohang, Republic of Korea, takes this approach to tackle the problem. He starts by assuming that the prediction given by QFT is correct, allowing Λ to take on the immensely large value it predicts (Journal of Cosmology and Astroparticle Physics 2018 034). “Using modern cosmological observations from type Ia supernovae and the CMB, we can measure the total energy density of the universe, including the vacuum energy,” Appleby explains. “The value obtained from these measurements is tiny compared to particle-physics scales.”
This is because, according to QFT, every particle in the universe should contribute to vacuum energy, thus exerting a negative pressure that is driving the expansion of the universe. The problem is that given the estimated number of particles in the universe, as well as the virtual particle pairs that pop in and out of existence in empty space, vacuum energy should be accelerating the expansion much faster than astronomers see in the redshifts of supernovae (figure 2).

QFT says the value of this contribution is given by the mass of the particles, which are well known, meaning there isn’t a problem with this aspect of QFT. As an example of this radical difference between the contribution to dark energy and the cosmological constant that QFT says particles should make, and the value that we actually observe, Appleby cites the electron and Higgs boson. Based on their masses, the contributions made solely by these particles to the vacuum energy of the universe should be roughly 40–60 orders of magnitude greater than our astronomical measurements suggest.
Assuming that the value provided by QFT is correct, Appleby and his collaborator Eric Linder from the University of California, Berkeley, have to explain why the observed value is so diminutive. They do this by refining the idea of gravity itself. “We asked the question: can we construct a theory of gravity that possesses low energy vacuum states, via lower particle contributions, despite the large cosmological constant?” explains Appleby. “Our analysis shows that such a theory can be constructed, but only by introducing additional gravitational fields to models of the universe.”
Appleby and Linder have constructed a general class of gravitational models, which suggests that vacuum energy is present, but doesn’t affect the curvature of space–time. This results in a space–time that looks like our low-energy universe, not one with the huge vacuum energy of QFT. “We pick out particular gravity models with the behaviour that we are searching for,” he continues. “Vacuum energy is present in our approach, but it does not affect the curvature of space–time. It does gravitate, but its effect is purely felt by the new gravitational field that we have introduced. In this approach, the cosmological constant problem becomes moot because it can take any value, but its effect is not felt directly.”
The strength of the model – which the duo label as “the well-tempered cosmological constant” – is that no energy scales have to be fine-tuned within it. As the vacuum energy in their models doesn’t impact the curvature of space–time, the individual contributions of particles would not influence the redshift of supernovae, thereby doing away with the observational disparity. Therefore, the vacuum energy in their model can be whatever value that QFT and particle physics predicts, without conflicting with observed values from astronomy. This energy can even change due to a phase transition.
Despite this utility, Appleby, like García, accepts that the model he and Linder proposed isn’t perfect and needs to be refined. “The main issue with our work is that we have to introduce new gravitational fields, which have not yet been observed, and the kinetic energy and potential of these additional fields must take a very particular form,” he says. “It is an open question whether such a field can be embedded in some more fundamental quantum gravity model.”
Appleby also points out that his model requires a revision of GR, which is a hugely successful theory of gravity. Indeed, GR is supported by a wealth of experimental evidence both here on Earth and beyond the limits of the Milky Way. “When you modify gravity in some way, you have to show that this new theory can also pass the same stringent observational tests that GR has,” Appleby concedes. “This is a difficult hurdle for any gravity model to overcome, and we must perform these checks in the future.”
Tuning in to the cosmological constant problem
Seeking to adjust theories of gravity to account for the cosmological constant problem is also an approach that has been considered by Lombriser over in Geneva. “My research in this area started out with investigating modifications to Einstein’s theory of GR as an alternative driver of the late-time accelerated expansion of our cosmos to the cosmological constant,” explains Lombriser. “In 2015 I realized that for modifications of the theory of gravity to be the direct cause of cosmic acceleration, and not violate cosmological observations, the speed of gravitational waves would have to differ from the speed of light. That did not sound right, and I started to focus on different explanations.”
Lombriser has begun to explore the idea that while modifications to GR or scalar energy fields may not be responsible for directly causing the late-time acceleration, they could instead “tune” the cosmological constant to do so. “I was surprised that I did not even have to modify Einstein’s equations to solve the problem,” says Lombriser. “I simply had to perform an additional variation with respect to a quantity that already appears in the equations – the Planck mass, which represents the strength of the gravitational coupling.”
The variation results in an additional equation, one which constrains Λ to the volume of space–time in the observable universe (Phys. Lett. B 797 134804). It also explains why vacuum energy can’t freely gravitate. Lombriser adds that by evaluating this constraint equation with some minimal assumptions about our place in the cosmic history, he and his colleagues can estimate the value that Λ occupies in our current cosmic energy budget. They have found this to be 70% in agreement with the dark energy contributions suggested by observations.
“The model solves both the old and new aspects of the cosmological constant problem,” Lombriser explains. “The old problem of the gravitating vacuum energy and the new problem of the cosmic acceleration with a small cosmological constant, results in this strange coincidence of us happening to live at a time where the energy density is comparable to that of the cosmological constant. A clear strength of the model is its simplicity.”
Lombriser also accepts there are elements to the solution that he puts forward that are flawed or need refinement. In particular, he points to the fact that, due to its similarity to standard theory, the model he suggests may be impossible to falsify. “I think the way forward here is to see whether this new approach can be extended to naturally explain other poorly understood phenomena, such as producing a natural inflationary phase in the early universe,” he says. “Or we can investigate how the self-tuning mechanism appears from fundamental theory interactions. These could give rise to yet unknown phenomena that may be testable in the laboratory.”
The “vanilla” appeal of the cosmological constant
Of course, the three ideas discussed here could prove to all be theoretical dead-ends – a leap too far for researchers who have become accustomed to the mystery of the cosmological constant.
Indeed, Λ could remain a problem for descriptions of the universe and its expansion for decades to come. “This cosmological constant is like vanilla ice cream, it is very good, but kind of boring,” Garnavich concludes. “Removing it will make the house fall down unless there is a better theory to replace it.”
This will likely result in more exciting “flavours” of ideas, theories and models until a satisfactory explanation for the cosmological constant problem is found. When it comes to cosmology and science in general, there is definitely a benefit to the approach of “nothing ventured, nothing gained”. As Einstein himself perfectly captured this ethos: “A person who never made a mistake never tried anything new.”




