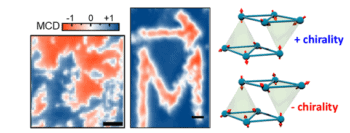
Materials that conduct electricity on their outsides, but not their insides, were once thought to be unusual. In fact, they’re ubiquitous, as Maia Vergniory of the Max Planck Institute for Chemical Physics of Solids in Dresden, Germany, and colleagues recently demonstrated by identifying tens of thousands of them. She spoke to Margaret Harris about how the team created the Topological Materials Database and what it means for the field
What is a topological material?
The most interesting topological materials are topological insulators, which are materials that are insulating in the bulk, but conducting on the surface. In these materials, the conducting channels where the electronic current flows are very robust. They persist independently of some external disturbances that one can have in experiments, such as weak disorder or temperature fluctuations, and they’re also independent of size. This is very interesting because it means these materials have a constant resistance, a constant conductivity. Having such tight control of the electronic current is useful for many applications.
What are some examples of topological insulators?
The best-known example is probably gallium arsenide, which is a two-dimensional semiconductor that is often used in experiments on the integer quantum Hall effect. In the newer generation of topological insulators, the best-known one is bismuth selenide, but this has not gained as much widespread attention.
Why did you and your colleagues decide to search for new topological materials?
At the time, there were just a few of them in the market, and we thought, “Okay, if we can develop a method that can calculate or diagnose topology quickly, we can see if there are materials that have more optimized properties.”
One example of an optimized property is the electronic band gap. The fact that these materials are insulating in the bulk means that in the bulk, there is a range of energies where the electrons cannot pass through. This “forbidden” energy range is the electronic band gap, and electrons cannot travel in that region even though they can exist on the material’s surface. The larger the material’s electronic band gap is, the better a topological insulator it will be.
How did you go about looking for new topological materials?
We developed an algorithm based on a material’s crystalline symmetries, which is something that was not taken into account before. The symmetry of the crystal is very important when dealing with topology because certain topological materials and some topological phases need a particular symmetry (or lack of symmetry) to exist. For example, the integer quantum Hall effect needs no symmetries at all, but it does need one symmetry to be broken, which is time-reversal symmetry. That means the material needs to be magnetic, or we need a very large external magnetic field.
But other topological phases do need symmetries, and we managed to identify which symmetries they were. Then, once we had all the symmetries identified, we could classify them – because in the end, that is what physicists do. We classify things.
We started working on the theoretical formulation in 2017, and two years later, we published the first paper related to this theoretical formulation. But it’s only now that we’ve finally completed everything and published it.
Who were your collaborators in this effort and how did each person contribute?
I designed (and, in part, performed) the first-principles calculations in which we considered how to simulate real materials and “diagnose” whether they had topological properties. For that, we used state-of-the-art codes and homemade codes that tell us how the material’s electrons behave and how we can classify the material’s topological properties. The theoretical formulation and analysis was done by Benjamin Wieder and Luis Elcoro because they are more hardcore theoretical physicists. They helped with analysing and classifying the topological phases. Another very important contributor and the leading guy of this project was Nicolas Regnault; we built up the website together and took care of designing the website and the database.
We also had help from Stuart Parkin and Claudia Felser. They are materials experts, so they could give us advice on whether a material was suitable or not. And then Andrei Bernevig was the co-ordinator of everything. We’d been working together for several years already.
And what did you find?
What we found is that there are many, many materials that have topological properties – tens of thousands of them.
Were you surprised by the number?
Yes. Very!
Given how ubiquitous these topological properties turned out to be, it seems almost surprising that you were surprised. Why hadn’t anyone noticed before?
I don’t know why it was missed completely by the community, but it’s not only our community within materials science and condensed-matter physics that missed it. Quantum mechanics has existed for a century already, and these topological properties are subtle, but they are not very complex. Yet all the smart “fathers” of quantum mechanics completely missed this theoretical formulation.
Has anybody tried synthesizing these materials and checking to see whether they do indeed behave as topological insulators?
Not all of them have been checked, of course, because there are so many. But some of them have. There are new topological materials that have been created experimentally following this work, like the high-order topological insulator Bi4Br4.
The Topological Materials Database you and your colleagues constructed has been described as “a periodic table for topological materials”. What properties determine its structure?
The topological properties are related to the electronic current, which is a global property of the material. One of the reasons physicists might not have thought about topology before is that they were very focused on local properties, rather than global ones. So in this sense, the important property is related to the localization of the charge and how the charge is defined in real space.
What we found is that if we know the material’s crystalline symmetries, we can anticipate what the behaviour of the charge is going to be or flow. And that is how we could classify the topological phases.
How does the Topological Materials Database work? What do researchers do when they use it?
First, they enter the material’s chemical formula. For example, if you are interested in salt, the formula is sodium chloride. So you put NaCl in the database and you click, and then all the properties appear. It’s very simple.
Wait, are you saying that common table salt is a topological material?
Yes.
Really?
Yes.
That’s amazing. Apart from surprising people with the topological properties of familiar materials, what impact do you hope your database will have on the field?
I hope it’s going to help experimentalists figure out which materials they should grow. Now that we have analysed the full spectrum of all material properties, experimentalists should be able to say, “Okay, this material is in an electron transport regime that we know is not good, but if I dope it with some electrons, then we will reach a very interesting regime.” So we hope, in a sense, that it will help experimentalists to find good materials.
A lot of attention has come to topological materials recently because of a possible link to quantum computing. Is that a big motivator in your work?
It’s related, but every field has different branches, and I would say our work is in a different branch. Of course, you need a topological material as a platform to develop a topological quantum computer using any of the possible qubits (quantum bits) that have been proposed, so what we did is important for that. But developing a topological quantum computer will require a lot more work on materials design because the material’s dimension plays an important role. We were looking at three dimensions, and it could be that for quantum computing platforms, we’d need to focus on 2D systems.
There are other applications, though. You could use the database to find materials for solar cells, for example, or for catalysis, detectors or low-dissipation electronic devices. Beyond the super-exotic applications, these day-to-day possibilities are also very important. But our real motivation for the work was to understand the physics of topology.
Ubiquity of topological materials revealed in catalogues containing thousands of substances
What’s next for you and your collaborators?
I would like to do research on organic materials. The focus in the current database is on inorganic materials because we took the Inorganic Crystal Structure Database as our starting point, but organic materials are very interesting, too. I’d also like to investigate more magnetic materials, because are fewer magnetic materials reported in the database than non-magnetic ones. And then I want to look at materials that have chiral symmetries – that is, they are symmetric, but “handed” in that they have a left version and a right version.
Do you think there could be thousands more topological materials out there among the organic or magnetic materials?
I don’t know. It depends on the size of the electronic band gap. We’ll see!
