For Italians, there’s nothing better to cheer you up than a bowlful of handmade pasta drizzled with extra-virgin olive oil and sprinkled with some good-quality Parmesan cheese. A mouthful of spaghetti perfectly rolled around your fork, they would argue, is without equal in the culinary world and can evoke a feeling of joy in even the hardest of souls. Indeed, rolling spaghetti around a fork is an art that every Italian is expected to learn from a young age. Mastering this skill takes years of practice, however, and children who’ve not yet got the knack will try to eat spaghetti by sucking up each spaghetto one at a time.

Vulgar and embarrassing though that might be, it is perfectly possible to eat a bowl of spaghetti in this way because each individual strand has two ends, meaning each can be pulled free from a pile of others. But what would happen if you were to eat a bowl of spaghetti in which each strand was not linear, but shaped into a ring? “Ring spaghetti” can’t be bought in the shops – in fact, as far as we’re aware, it’s never previously been served at any Italian dining table (though tiny pasta hoops can be bought). So to find out what happens, we decided to create our own ring spaghetti – or “anelloni” as we’ve decided to call it (anello in Italian meaning “ring”). Actually, we made our rings not from strands of spaghetti, which have a circular cross-section, but from linguine, which is flatter, but it makes no difference to anyone wishing to check the difference between ring-shaped and linear pasta. If you fancy trying the experiment in your own kitchen, we’ve included a simple recipe for anelloni (see below).

Faced with a dish of ring-shaped pasta like our anelloni, it turns out to be much harder to pull one piece of pasta free than if you were eating a plate of spaghetti, making the meal take longer. How much longer will depend on the length of the rings – and on your dexterity! We haven’t actually tried an experiment with anelloni of different sizes, but calculations show that as rings become longer, they can get more and more entangled with each other, with 100% of rings getting tangled up in the limit of infinitely long chains.

Running rings around pasta

Well, this is all very interesting, we hear you say – but what has pasta got to do with physics? Actually, strands of spaghetti (or linguine) are a very good macroscopic analogy of polymers – those long-chain molecules that make up everything from plastics to proteins. Normal spaghetti can be seen as an analogy for conventional “linear” polymers, such as polyethylene or polystyrene, while our novel ring-shaped pasta resembles ring polymers. These ring polymers are hard (though not impossible) to make synthetically, but they are more commonly found in nature.

For example, while DNA is a long double helix, pieces of DNA, known as plasmids, can be found as closed rings inside bacteria. Meanwhile, tiny single-celled organisms known as Kinetoplastida keep all their mitochondrial DNA as a mass of rings that are interlocked rather like the loops of metal on a medieval knight’s chainmail armour (mitochondria being objects in which chemical energy from food is turned into a form the cell can use). These rings, which are double-stranded sections of DNA, are different from rings of our anelloni pasta, which get tangled up but can, in principle, be pulled apart, even if it’s hard to do so. In fact, when Kinetoplastida divides, the only way it can physically separate the loops is to use a particular enzyme to cut each ring, which can then de-link from its neighbour before joining itself up again.

The thing about ring-shaped polymers, though, is that they’re very poorly understood – in fact, they’re one of the last big mysteries in polymer physics. Physicists are now pretty clear about how individual linear poly-mer molecules move: each chain slides along like a snake moving through tall grass in a process dubbed “reptation”. Similarly, suck on a strand of spaghetti and it’ll slither through the others in the bowl and up into your mouth. But reptation doesn’t apply to rings because they have no free ends. There are theories conjecturing how rings move and what shape they adopt, but none really captures the whole story.

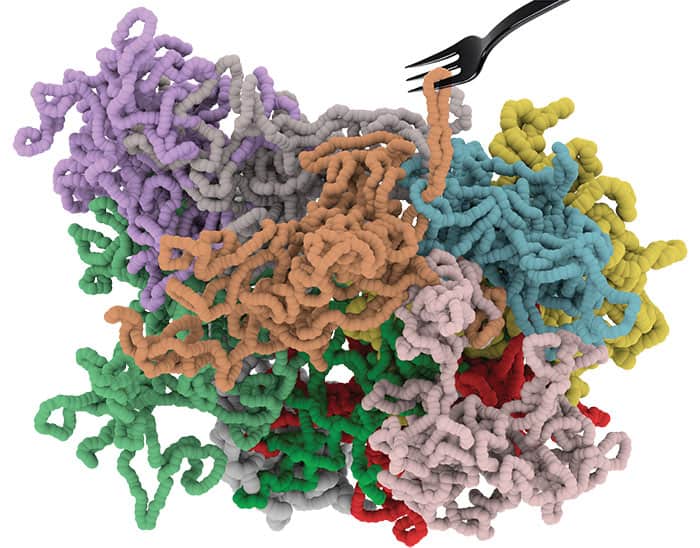
In our work, we are interested in knowing what shapes ring polymers adopt when placed in a gel of linear polymers, which we model as a 3D lattice of obstacles. As each ring polymer must form a continuous loop that weaves itself between the obstacles, the ring polymers don’t stay circular but end up adopting some curious shapes dubbed “lattice animals” because they can, rather amusingly, look like real animals. While the idea of ring polymers forming these lattice-animal shapes is rather cute, the fact that individual ring polymers must stay as isolated loops (known as “un-knots” in the language of topology) is what makes studying these materials really hard.

Ring polymers are free to adopt different configurations and don’t necessarily stay circular but can crumple up into different shapes. Unlike linear polymers, in which you can just examine all the local interactions between individual segments, or “monomers”, of the molecule in isolation, for ring polymers you have to keep track of the overall topological state of the chain. Judging the likelihood of a ring polymer adopting a particular configuration is therefore much more tricky and what makes studying these molecules hard.

Recent computational studies of the dynamics of ring polymers have revealed that these macro-molecules can entangle in a very different way from their linear cousins. Because of their topology, ring polymers can form horribly complicated structures, in which one ring is threaded through another, which is threaded through another and so on to form what we call “hierarchical threadings”. The most tightly bound ring in this giant network can only get free if the other rings are pulled apart one by one in a particular order.

Towards a topological glass

The bottom line is that the individual ring polymers in a network find it very hard to move freely even though they don’t actually form any knots, which are topological states that can only be undone by cutting the ring (see figure 1, above). In fact, recent simulations that we’ve carried out suggest that if they are long enough, ring polymers become so sluggardly that they could eventually appear frozen into place. If this were to occur – and we have evidence, though no definite proof, that it does – we would have identified a new state of matter, which we have called a “topological glass” (2014 ACS Macro Lett. 3 255 and 2013 Europhys. Lett. 102 58005).

Ordinary glassy materials are made by cooling a viscous liquid, with the amount of movement dropping exponentially as temperature falls; it becomes a glass only once the material is cool enough that the molecules in it have stopped moving. A topological glass made from ring polymers would be rather different: the motion would slow down exponentially not just with temperature but with ring length too. Despite not yet having definite proof that such a state exists, we have shown with our simulations that ring polymers certainly start to slow down in exactly the way you’d expect if it were a true topological glass. What’s holding us back from getting a definitive answer is computer power: as the rings get longer and more tangled up, the time it takes to probe the motion rises exponentially, though we’ve recently bid for more supercomputer time to push our simulations to the limit.

“Topological phases” are all the rage in condensed-matter physics these days, with researchers studying exotic materials such as topological insulators (materials that don’t conduct electrically in the bulk but do along the edge) and rod-shaped liquid-crystal molecules that contain topological defects. What would be nice about a topological glass is that its properties would be governed purely by topology, rather than the system-specific chemical details that often control when and how classical glasses form. Physicists love that kind of universal behaviour – in fact, obtaining a universal description of glasses has been a central goal in condensed-matter physics for several decades. What’s more, ring polymers could also inspire the design of novel materials that could have applications that we cannot yet even imagine.

So while we are not entirely sure yet that topological glasses really do exist, what we do know from our research is that when it comes to eating pasta, the Italians were right all along – you’re better off sticking to spaghetti, which you can eat nice and quickly. Make yourself a bowl of anelloni and it’s likely to have gone cold by the time you’ve pulled all the rings apart and struggled your way to the messy end.

A recipe for anelloni

Serves two.

Ingredients

2 eggs 200 g plain flour Extra-virgin olive oil Aged Parmesan

Method

• Shape the flour into a mound on a clean surface and make a large well in the middle.
• Add the eggs bit by bit to the flour and mix until you get a smooth dough, taking care to avoid the dough becoming clumpy.
• Knead rigorously by hand for 15–20 min until the dough is smooth and elastic.
• Flatten the dough out with a rolling pin to form a thin sheet.
• Cover one half of the sheet with a piece of baking paper so that the dough doesn’t stick as you take one end of the sheet and fold it over itself, making sure it overlaps by about 1 cm.
• Moisten the overlapped region with water and then seal the sheet together to create a flat, open cylindrical shape (see image above).
• Using scissors, cut thin strips along the dough at 90° to the sealed edge to form closed rings of pasta, or anelloni (see image above).
• Cook for 3–5 min in plenty of boiling water.
• Enjoy it with a generous drizzling of olive oil and lots of Parmesan!