Topological defects in the structure of materials known as active nematics can act as rods that mix the fluids – much like one might mix colours in white paint. This is the new finding from researchers at the University of California, Merced, who say that the mixing is a result of sliding on a molecular scale. The work, which has applied chaotic advection to the emerging field of active matter for the first time, could help advance our fundamental understanding of how defects move collectively in liquid crystals.
Nature abounds with examples of active matter, with some well-known examples being flocks of birds, fish and insects, sheets of biological cells and swarms of bacteria. Researchers have been trying to make biomimetic and synthetic active materials in the laboratory from materials such as self-propelled colloids and dense phases of mechanically driven biopolymers. Needless to say, they would like to better understand the fundamental physics of these systems.

“Intriguing” non-equilibrium systems
“Active matter is attracting a huge amount of research interest at the moment,” says co-team leader Linda Hirst.
“They are intriguing because they are non-equilibrium systems (which cannot be described in the framework of conventional thermodynamics) in which energy is injected on the microscale throughout the structure, ultimately giving rise to macroscopic coherent motion,” adds co-team leader Kevin Mitchell. This large-scale motion can produce emergent structures such as phase boundaries and topological defects, where local order breaks down.
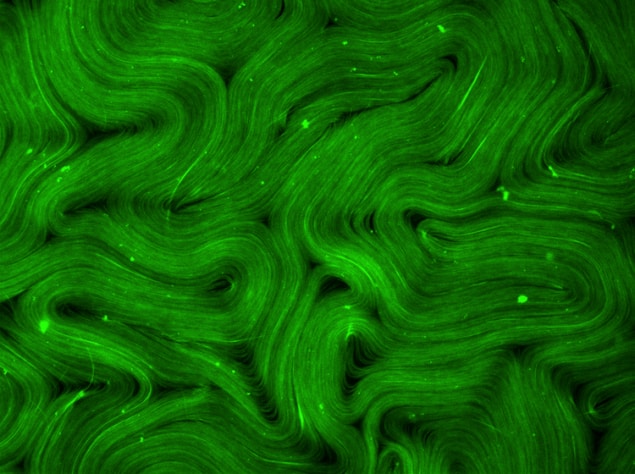
In their work, Mitchell, Hirst and colleagues studied active nematic fluids, which are a new class of soft materials that can be formed from anisotropic molecules such as biological filaments (as in this work). The fluid they investigated comprises two basic components, both found in biological cells: microtubules and kinesin motors. Microtubules are filaments of long, semi-flexible protein assemblies and the researchers could see bundles of these filaments sliding past each other in microscopy images. Kinesin is a protein that can convert chemical energy, in the form of ATP, to mechanical energy.
“The kinesin molecule has two binding sites (or ‘feet’) that bind and unbind to a microtubule one after the other, to produce a ‘walking’ motion along the microtubule,” explains Hirst. “In our fluid, pairs of motors are connected back-to-back so that the feet of the two motors walk on two different microtubules.”

Large-scale advection
This process produces a shearing motion between the neighbouring microtubules that causes the filaments to extend past each other, effectively stretching the fluid locally in the direction of the microtubule, she adds. As the material stretches, topological defects spontaneously appear and cancel each other out, generating large-scale advection in the fluid. “This material was originally invented by Prof. Zvonimir Dogic when he was at Brandeis, and who is now at UC Santa Barbara.
“There aren’t many examples of active nematics that we can use in the lab,” she says. “We wanted a small-scale system in which we could observe fluid behaviour but one that was large enough to allow us to observe individual elements (with fluorescence microscopy, for example). We chose to work with the microtubule/kinesin system because it is the only example to date of a molecular-level extensile active nematic that can remain in a steady state for long periods.
“The fact that we were able to collaborate with the material’s inventor and receive materials from the Brandeis biomaterials facility was also an important factor for us when making our choice.”
The Lyapunov exponent and topological entropy
The researchers studied the self-driven advection and mixing on different length scales in their system using two techniques. They measured stretching on the local scale by the Lyapunov exponent and more large-scale mixing by analysing the way in which the topological defects move around one another.
“The Lyapunov exponent is a quantity employed in chaos theory,” explains Mitchell. “It describes how quickly two points in the fluid move away from one another and is thus very closely related to the extensile, or stretching, nature of the material.”
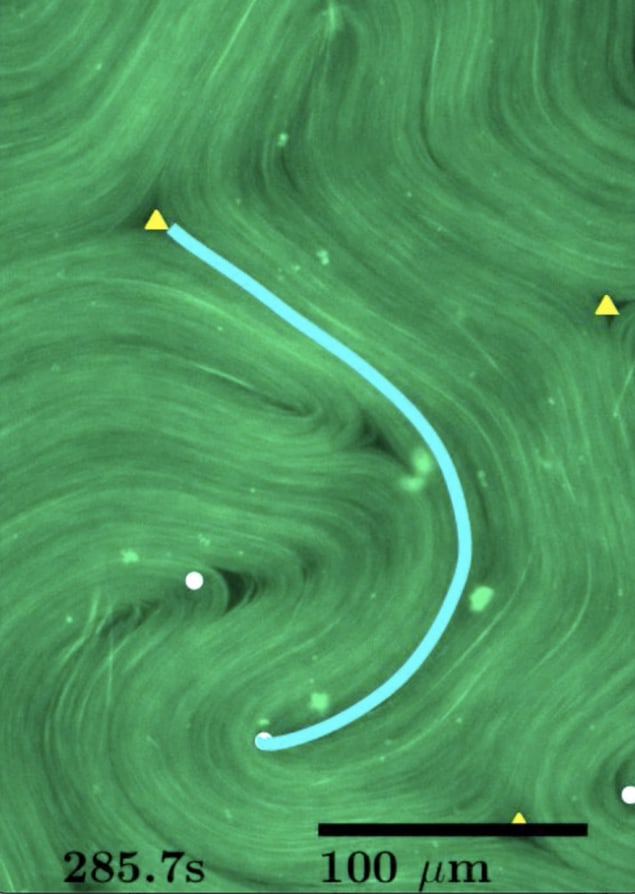
The researchers say they measured the Lyapunov exponent using the velocity-gradient at every point in their system.
For larger scale measurements, they used the analogy between the motion of the defects and patterns of braided strings. They did this by adapting ideas from braid theory in mathematics to compute the amount of stretching in the fluid (or the topological entropy) caused by the motion of the defects. “Quantitatively, we found that the topological entropy and the Lyapunov exponent were quite close to one another, with the former being slightly larger than the latter,” Mitchell tells Physics World. “We were quite pleased with this agreement since theory predicts that the topological entropy is an upper bound to the Lyapunov exponent in systems like ours.”
Studying the effects of confinement
The researchers say they are “excited” about bringing together the two disciplines of active nematics and chaotic advection and believe that studies like theirs will continue to provide new insights into both fields.

Amyloid fibrils undergo liquid-crystalline phase transitions
They will now be focusing on studying the effect of confinement on chaotic mixing in their active nematic. “For example, what happens when the material is confined to wells of different geometries or to channels?” asks Hirst. “Can we control the topological entropy by tuning either the confining geometry or by other external factors?”
“We are also interested in studying the fractal patterns displayed by our system and what their physical origins might be,” adds Mitchell.
Full details of the research are reported in Nature Physics 10.1038/s41567-019-0600-y.