A deep-learning system that can sift gravitational wave signals from background noise has been created by physicists in the UK. Deep learning is a neural-inspired pattern recognition technique that has already been applied to image processing, speech recognition and medical diagnoses, among other things. Chris Messenger and colleagues at the University of Glasgow have shown that their system is as effective as conventional signal processing and has the potential to identify gravitational-wave signals much more quickly.
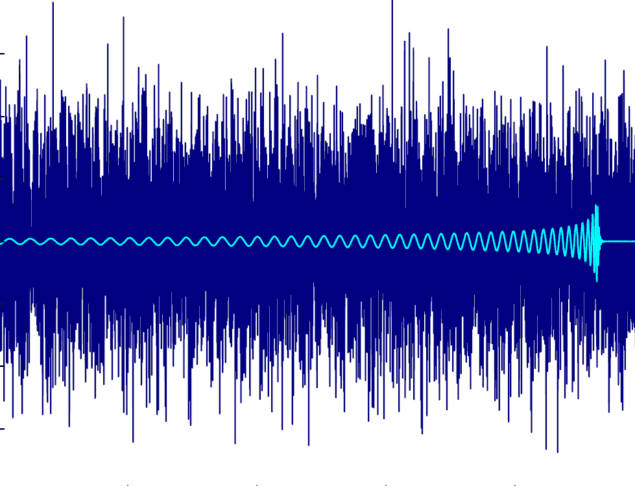
Gravitational waves are ripples in space-time that can be observed using the LIGO-Virgo detectors – which are laser interferometers with pairs of arms several kilometres long positioned at right angles to each other. As a wave passes through the Earth it very slightly stretches one arm while squeezing the other, before squeezing the first and stretching the second, and so on. This generates a series of tiny but distinctive oscillations that are recorded as variations in the interference patterns measured by the instruments.
The first gravitational wave to be detected was snared by the two LIGO detectors in the US in September 2015. Unlike signals observed since then, these oscillations were visible to the naked eye within the raw data. Normally gravitational-wave signals are swamped by noise – seismic, thermal motion or photon statistics – that must be filtered out using computer algorithms if the signal is to emerge.
Template matching
Usually signals are picked out from the noise using a technique known as matched filtering. This involves comparing the oscillations recorded by the interferometer with a series of templates representing waveforms produced by different astrophysicals event that are calculated using post-Newtonian and relativistic equations. A significant match between the observational data and any of the templates means a detection, while the type of waveform in the template reveals what caused the gravitational wave in question.
However, the need to compare large numbers of templates to ensure an accurate result means that matched filtering requires lots of processing power and is time-consuming. In the latest work, the team has shown they can potentially reduce the time needed – by using machine learning rather than conventional algorithms. Their system relies on a neural network, which, like the brain, consists of layers of processing units that fire when they receive a certain input.
The system’s input layer holds the raw data that would come from an interferometer – a series of numbers related to variations in the arms’ strain. These data are fed to the first of nine internal layers made up of neurons whose output depends on the input data and a weighting applied to each neuron. With those outputs then forming the inputs of the next layer, and so on, the system ends in a final layer consisting of just two neurons that each generate a probability value between 0 and 1. One neuron reveals how likely it is that the raw data contain a signal while the other, conversely, describes the likelihood of it containing just noise.
Training weights
Initially the neurons’ weights are set randomly and the system is “trained” by exposing it to a series of sample data sets, half of which consist of a gravitational-wave signal from binary black-hole mergers covered by “Gaussian” noise while the other half contain Gaussian noise only. The probability values computed by the system in each case are compared with the (known) data type – signal or noise – and the degree of error is then used to adjust the neuron weights layer by layer in a process called back propagation. The idea is that after enough iterations, the network can distinguish signal from noise reliably.
Having trained their system with half a million data sets, Messenger and co-workers then fed it 20,000 new waveforms to see how many it could correctly identify. They also analysed the same set of waveforms using matched filtering. They found that the two techniques performed nearly equally – their ability to find the buried signals depending in a very similar way on the signal-to-noise ratio and on the probability of mistaking noise for signal. However, because the bulk of computation for deep learning occurs during training, the new technique was far quicker – taking just a few seconds to analyse all the unknown waveforms rather than several hours.
According to Glasgow group member Hunter Gabbard, this greater speed might prove handy as interferometers become more sensitive and detect gravitational waves more often. This, he says, could help alert astronomers to signals from merging neutron stars so that they can point their telescopes to the patch of sky in question and pick up the accompanying electromagnetic radiation before it disappears.
Recognizing glitches
The Glasgow group, however, is not the only one to have applied artificial intelligence to gravitational-wave detection. In particular, Daniel George and Eliu Huerta of the University of Illinois in the US have already published two papers showing that deep learning can operate orders of magnitude faster than matched filtering. They have also used their neural network to estimate properties of gravitational-wave signals, such as the masses of radiating black holes, as well as analysing real, as opposed to simulated, LIGO data. Such data, they point out, can contain what are known as glitches – noise that can mimic a signal – as well as purely Gaussian noise.
LIGO detects first ever gravitational waves – from two merging black holes
Rory Smith of Monash University in Australia is slightly more cautious about the potential for deep learning. He says it “could one day show promise”, suggesting it might prove particularly useful for distinguishing astrophysical signals from glitches, but prefers to develop more physics-based “principled” approaches. “There’s still a lot of room to better understand the signals and data that we have without resorting to black-box techniques,” he argues.
Messenger and colleagues describe their work in Physical Review Letters.




