Soon after the invention of the laser in the late 1950s many dubbed the discovery as “a solution in search of a problem”. Nowadays lasers are used in an enormous range of scientific and technological applications, thanks to their high intensity and their ability to emit light in an extremely narrow range of wavelengths. Indeed, the laser has revolutionized the whole field of optics and now plays a central role in the world’s communications networks. The market for lasers, optical amplifiers and other optoelectronic components is worth billions of dollars every year.

Atomic physicists are hoping that the invention of the “atom laser” will spark a similar revolution in the field of atom optics, or matter-wave optics as it is also known. Researchers in this field have relied heavily on the analogy between light and the wave-like nature of atoms. Lenses, mirrors and beam splitters have all been developed to control atomic beams just as their optical counterparts manipulate light. But what has been lacking in atom optics, until recently, is a source capable of producing an intense, highly directional, coherent beam in which all the atoms have the same wavelength just like the photons in a laser beam. This would be an atom laser.

Bose-Einstein basics

The idea for an atom laser predates the demonstration of the exotic quantum phenomenon of Bose-Einstein condensation in dilute atomic gases. But it was only after the first such condensate was produced in 1995 that the pursuit to create a laser-like source of atomic de Broglie waves became intense.

In a Bose condensate all the atoms occupy the same quantum state and can be described by the same wavefunction. The condensate therefore has many unusual properties not found in other states of matter. So why can we think of a Bose condensate as a coherent source of matter waves? To address this crucial point we have to remind ourselves of some of the physics behind the properties of laser light.

In a laser all the photons share the same wavefunction. This is possible because photons have an intrinsic angular momentum, or “spin”, of the Planck constant h divided by 2p. Particles that have a spin that is an integer multiple of h/2p obey Bose-Einstein statistics. This means that more than one so-called boson can occupy the same quantum state. Particles with half-integer spin – such as electrons, neutrons and protons, which all have spin h/4p – obey Fermi-Dirac statistics. Only one fermion can occupy a given quantum state.

A composite particle, such as an atom, is a boson if the sum of its protons, neutrons and electrons is an even number; the composite particle is a fermion if this sum is an odd number. Sodium-23 atoms, for example, are bosons, so a large number of them can be forced to occupy the same quantum state and therefore have the same wavefunction. To achieve this, a large number of atoms must be confined within a tiny trap and cooled to submillikelvin temperatures using a combination of optical and magnetic techniques (see “Bose condensates make quantum leaps and bounds” and Townsend, Ketterle and Stringari in further reading).

In this article we will concentrate on the properties of the condensates rather than on their creation. An important property of laser light is that it is monochromatic. By analogy, in a Bose-Einstein condensate all the atoms have the same energy and hence the same de Broglie wavelength. If this property can be maintained when the atoms are released from the condensate, we will have a highly monochromatic source of matter waves.

Another important property of laser light is that its intensity remains very stable. This property (called second-order coherence, which is discussed below) is rarely exploited in practical applications, but it is a feature that distinguishes a laser from a thermal light source, such as a filament lamp.

Output coupling

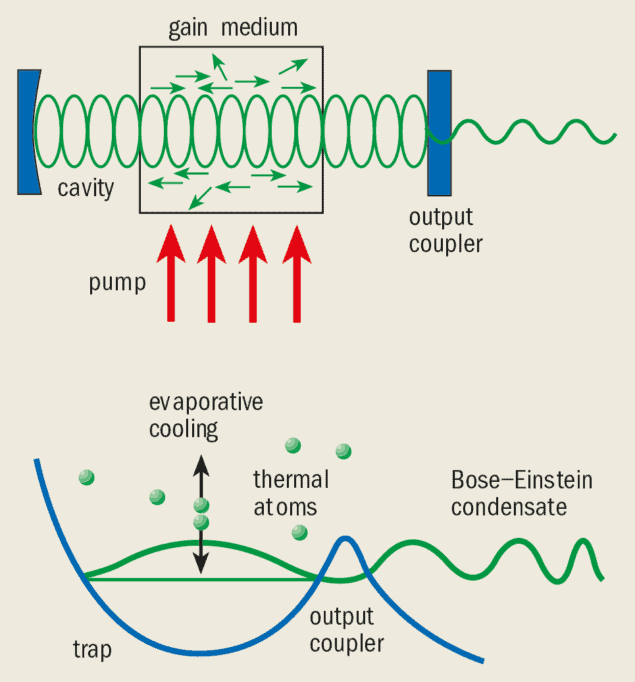
Bose-Einstein condensates are produced in confining potentials such as magnetic or optical traps by exploiting either the atoms’ magnetic moment or an electric dipole moment induced by lasers. In a magnetic trap, for instance, once the atoms have been cooled and trapped by lasers, the light is switched off and an inhomogeneous magnetic field provides a confining potential around the atoms. The trap is analogous to the optical cavity formed by the mirrors in a conventional laser (see figure 1).

But to make a laser we need to extract the coherent field from the optical cavity in a controlled way. This technique is known as “output coupling”. In the case of a conventional laser the output coupler is a partially transmitting mirror. Output coupling for atoms can be achieved by transferring them from states that are confined to ones that are not, typically by changing an internal degree of freedom, such as the magnetic states of the atoms.

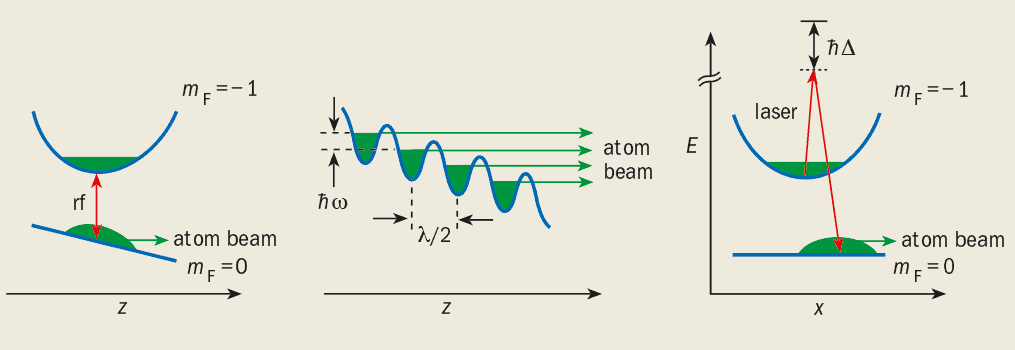
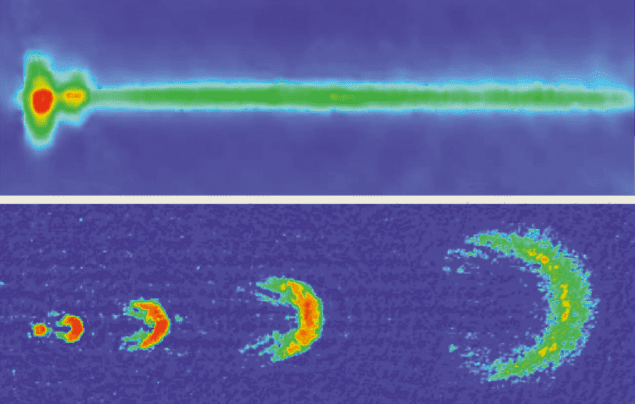
The first demonstration of atomic output coupling from a Bose-Einstein condensate was performed with sodium atoms in a magnetic trap by Chris Townsend, Wolfgang Ketterle and co-workers at the Massachusetts Institute of Technology (MIT) in 1997. Only the atoms that had their magnetic moments pointing in the opposite direction to the magnetic field were trapped. The MIT researchers applied short radio-frequency pulses to “flip” the spins of some of the atoms and therefore release them from the trap (see figure 2c). The extracted atoms then accelerated away from the trap under the force of gravity. The output from this rudimentary atom laser was a series of pulses that expanded as they fell due to repulsive interactions between the ejected atoms and those inside the trap (see figure 3a).

In the MIT experiment, fluctuations in the confining magnetic field caused variations in the frequency needed to flip the spins of the atoms in the trap. To get round this problem, the radio-frequency field was pulsed on a timescale that was short compared with the period over which the magnetic field changed. The short, pulsed nature of the output coupling meant that the coherence length (i.e. the distance over which the matter waves remained “in step”) was limited to the length of the condensate itself. However, the coherence length can be increased by essentially “dribbling” the condensate out of the trap using a low rate of continuous output coupling.

Recently Theodor Hänsch and colleagues at the Max Planck Institute for Quantum Optics in Munich extracted a continuous atom beam that lasted for 0.1 s. The Munich team used radio-frequency output coupling in an experimental set-up that was similar to the one at MIT but used more stable magnetic fields (see figure 3b).

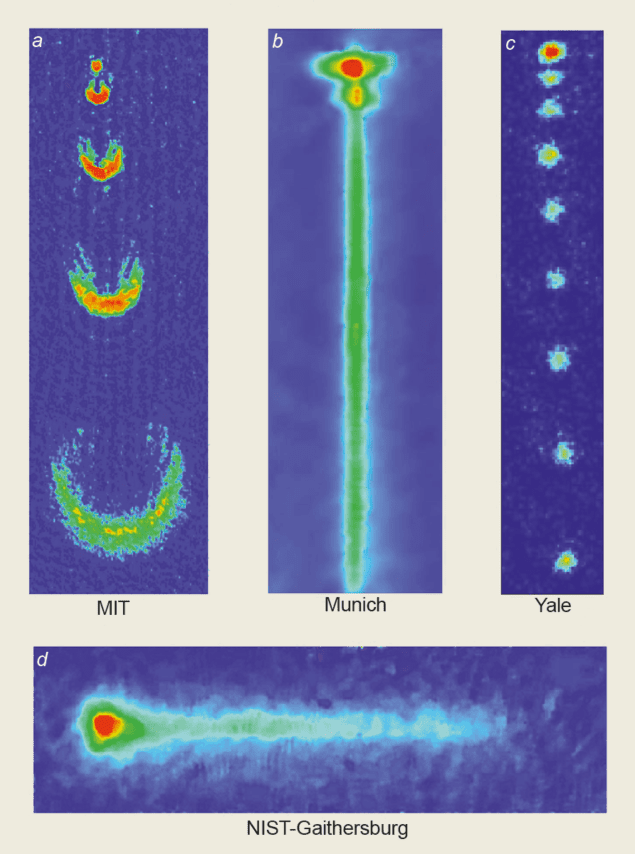
In 1998 Brian Anderson and Mark Kasevich at Yale University in the US demonstrated how to extract atoms from a one-dimensional, periodic optical trap, known as an optical lattice. Two laser beams pointing in opposite directions interacted to form a standing wave that trapped the atoms in the vertical direction. The optical potential was sufficiently shallow that the atoms were able to both tunnel out of the traps and accelerate away via gravity (see figure 2b). The Yale team loaded the optical lattice with atoms from a Bose-Einstein condensate. This meant that the atoms that escaped from each trap were “phase coherent” i.e. the phases of the matter waves were correlated. The series of downward-falling output pulses was akin to the output of a mode-locked, pulsed laser (see figure 3c).

A new output-coupling technique was recently demonstrated by two of the authors (William Phillips and Kristian Helmerson) and colleagues at the US National Institute of Standards and Technology (NIST) in Gaithersburg, Maryland. The atoms were extracted from a magnetic trap, using an optical technique known as stimulated Raman scattering, to change the quantum state of the condensate atoms from one that is confined to one that is not. The condensate atoms absorb photons at one wavelength and emit photons at a slightly different wavelength (figure 2c). This gives the atoms a “momentum kick” away from the remaining trapped atoms. Both the magnitude and direction of the output beam can be selected by varying the orientation of the laser beams. Unlike the other output-coupling schemes, the NIST technique produces an atom laser that does not rely on gravity.

This output-coupling scheme has an additional advantage: the atoms in the beam have a transverse-momentum spread that is greatly reduced. In the other atom lasers repulsive interactions between the atoms cause a large momentum spread. In the NIST experiment, however, the atoms receive a large kick in the selected direction and spend little time in the presence of the other atoms, thereby reducing the problem.

The laser light used to release the atoms from the trap can be pulsed or continuous, just like the radio-frequency radiation in the other experiments. In the NIST experiments the magnetic field used to trap the atoms had a rotating component. The repetition rate of the output-coupling pulses was essentially synchronized to this rotating field. The rate was fast enough so that the clouds of atoms leaving the trap overlapped in a horizontal and essentially continuous beam (see figure 3d).

The coherence length of the various atom-laser beams has not been measured directly. Nevertheless, the NIST team has shown that two successive pulses are fully coherent over their pulse length, which is the size of the condensate. Because the output-coupling methods are coherent, it is likely that the coherence length of the lasers in figure 3 is in fact much larger than the size of the condensate.

Atom-laser theory

Theoretical studies of atom lasers have been stimulated by the increasing availability of experimental data. The challenge is to develop a quantum field theory of output coupling and then use it to optimize the design of practical systems. In 1998 Bernhard Kneer and colleagues at the University of Ulm in Germany developed a theoretical model that combined various aspects of optical-laser theory and the theory that describes static Bose-Einstein condensates. These treatments, however, do not fully address the question of the coherence of the output beam.

In reality, light and matter waves are not completely coherent – a fact that greatly complicates any theoretical description. The coherence of a condensate or output beam can be characterized using the theory of “partially” coherent matter-wave fields. The theory incorporates various so-called coherence functions that provide quantitative information about the coherence. The simplest of these, first-order coherence, tells us whether we can see interference fringes formed by two overlapping fields. Higher-order coherence functions can represent intensity correlations between fields, for example.

According to the theory, the matter waves output by an atom laser are coherent in two respects: they contain a narrow range of wavelengths and they are much more stable in intensity than thermal beams. In 1997 Robert Dodd and co-workers at NIST calculated the intensity stability for a trapped condensate within the framework of quantum field theory. We now need to do this for the flowing output from a condensate. Researchers at Oxford University are aiming to calculate the coherence functions for the output-coupling schemes mentioned earlier using so-called finite-temperature field theory. The aim of the work is to tune the output-coupler parameters to maximize the coherence of the atom-laser output.

An important challenge in building a continuous atom laser is to design an output-coupling scheme that keeps the phase of the matter waves “in step” over a long period of time. Suppose that we describe the matter wave by I(x,t) = A(x,t) cos(wt + f(x,t)) and we can keep the intensity, A, constant. The overall coherence of the output is then limited by the stability of the phase, f, over time and in space. If the phase wanders over time then it will also limit the line width of the atom laser via the uncertainty principle. Several theoretical studies to date have addressed the question of phase stability, while the stability of the condensate in real systems remains an area of active research.

Atom-laser applications

The possibility of producing a coherent beam of atoms that could be collimated to travel long distances, or brought to a tiny focus like an optical laser, opens up a whole host of applications. Although it would be imprudent to try to predict all of the applications that will arise, there are reasons to believe that the atom laser will be a significant scientific tool in the future. Atom lasers may have a major impact on the fields of atom optics, atom lithography, precision atomic clocks and other measurements of fundamental standards.

One application for which the coherence of an atom laser is critical is atom holography. Just as conventional holography uses the diffraction of a photon beam to reconstruct a 3-D image, atom holography uses the diffraction of atoms. As the de Broglie wavelength of the atoms is much smaller than the wavelength of light, an atom laser could create much higher resolution holographic images. Atom holography might be used to project complex integrated-circuit patterns, just a few nanometres in scale, onto semiconductors.

The first atom holograms were demonstrated in 1996 by Fujio Shimuzu and colleagues at the University of Tokyo, in collaboration with Jun-ichi Fujita at NEC Research, using laser-cooled atoms. However, the matter waves in these experiments were only partially coherent because the atoms were not all in the same quantum state.

In the case of laser-cooled gases, the level of coherence needed to create a hologram is achieved by selecting a small portion of the atoms. Although this increases the spatial coherence of the matter waves, it is at the expense of the flux or number of atoms available for the duration of the experiment (which is often determined by the overstretched patience of the graduate student). The problem would be alleviated by having a source in which most of the atoms are in the same quantum state. An atom laser is such a source and could provide a much more intense and fully coherent beam of atoms.

Holography is a two-step process. First, a hologram – a sort of diffraction grating containing information about the object – is produced. Then a beam of light (or atoms) is diffracted by the hologram to form the image. In optical holography, the hologram is often made by interfering a laser beam with light that has been reflected from an object. The resulting diffraction pattern is recorded on photographic film. However, the diffraction pattern can also be generated by computer, so that an image can be formed without ever actually using an object.

In the atom-holography experiments, an image has been created by diffracting a coherent beam of atoms through a grating that was manufactured using electron-beam lithography. The image was recorded on a “microchannel plate” – a detector that is sensitive to atoms. So far, atom holography has been able to produce 2-D images, and not the familiar 3-D ones of optical holography.

A related application, which might also benefit from a source of coherent matter waves, is atom interferometry. In an atom interferometer an atomic wave packet is coherently split into two wave packets that follow different paths before recombining. The interference pattern created when the two wave packets recombine tells us something about the phase difference between the two paths. Atom interferometers that are more sensitive than optical interferometers could be used to test quantum theory, and may even be able to detect changes in space-time (see Physics World March 1997 pp43-48). This is because the de Broglie wavelength of the atoms is smaller than the wavelength of light, the atoms have mass, and because the internal structure of the atom can also be exploited.

Until now, all atom-interferometry experiments have used thermal atomic beams, analogous to the lamps that were used in the early days of optics experiments. Filtering is typically used to reduce the energy spread of the beam and achieve the degree of coherence needed to see the interference effects. The coherence length, however, is short, limiting the use of atom beams to interferometers that have “arms” of equal length – otherwise the interference pattern would be washed out.

Atom lasers would allow the use of devices with unequal path lengths, such as Michelson interferometers. Such devices may provide a way to measure lengths over large distances with unprecedented precision.

Nonlinear atom optics

Just as the invention of the laser enabled the field of nonlinear optics to flourish, intense sources of coherent matter waves have opened up a similar field in atom optics. Until recently, most atom-optics experiments could be thought of as single-particle phenomena where the interactions between particles could be neglected. In 1993 Pierre Meystre and colleagues at the University of Arizona in the US considered a new kind of atom-optics experiment where interactions between the atoms were crucial. They called this new field “nonlinear atom optics”.

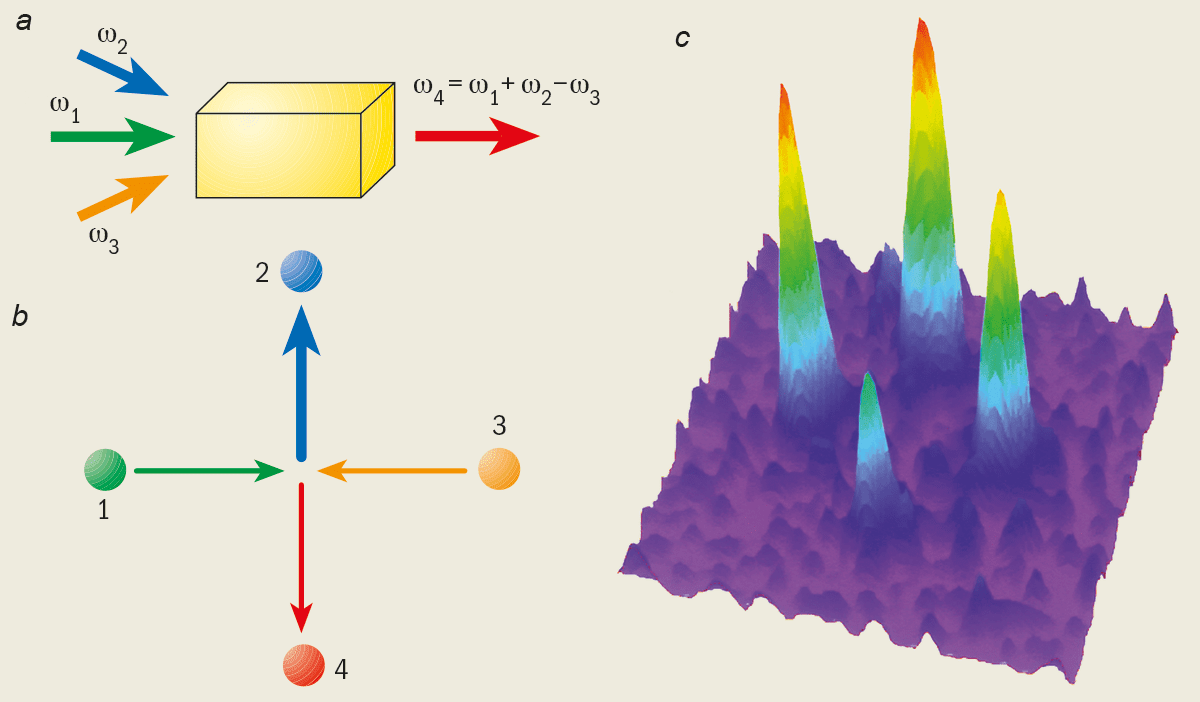
In conventional nonlinear optics, photons interact with each other through some mediating material, such as transparent crystal. A common nonlinear optical phenomenon is “four-wave mixing”. Here, three waves are sent into a nonlinear medium and the exchange of energy and momentum between the waves results in the production of a fourth wave (see figure 4). A quantum mechanical description of this process involves two photons from separate beams annihilating while two other photons are created. One of these photons adds to the third beam and amplifies it, while the other represents a new, fourth beam.

In 1998 Paul Julienne from NIST, and Marek Trippenbach and Yehuda Band from Ben-Gurion University of the Negev in Israel predicted that the nonlinear mean-field interactions between atoms in a Bose-Einstein condensate, like the one at NIST, could lead to four-wave mixing of matter waves. They predicted that if three condensates of appropriate momenta collided, the term in the nonlinear Schrödinger equation that describes the interactions between the atoms would give rise to a fourth. At the atomic level, this process can be described as a collision between two atoms from separate matter-wave beams. One of the atoms is stimulated so that it scatters in the direction of the third incident matter-wave beam. By the conservation of momentum, the other atom goes off to make a fourth, separate beam.

The actual experiment performed at NIST did not use three separate condensates. Instead, lasers were used to divide a single condensate into three different momentum states via a process called Bragg diffraction. This is similar to the stimulated Raman process described earlier, except that the atoms return to the same magnetic sublevel. However, the absorption and emission of photons gives the atom a momentum kick in a well defined direction.

Starting with a condensate at rest, two separate pulses of interfering laser beams were applied to create the Bragg “diffraction grating” that divided the atoms roughly equally into three different momentum states, including the state of the initial condensate. When these pulses were applied fast enough – that is before the different momentum states had a chance to separate – atoms in a fourth momentum state were produced (see figure 4c).

The future of atom lasers

Although we have touched on some of the future applications of atom lasers, most of them (and even those that we cannot predict) are likely to depend on future developments in atom lasers themselves. Again, using developments in optical laser technology as a guide, we speculate on some of the possible future directions of atom-laser research.

Most continuous-wave optical lasers are truly continuous in the sense that they are continually fed energy or “pumped” so that they can supply photons indefinitely. A truly continuous source of coherent matter waves could be similarly achieved only if the condensate could be replenished continually. Schemes for steady-state condensate formation have been devised but so far none has been demonstrated in the laboratory.

The cavity in an optical laser is typically many wavelengths long and as a result can support several different frequencies or modes. In a Bose-Einstein condensate, however, the atoms typically occupy the lowest energy state of the trap. It remains to be investigated whether condensates can be produced in higher-energy states and then extracted from the trap to give a higher-energy beam of atoms.

In recent years laser cooling and neutral-atom manipulation have developed into mature areas of atomic physics and have boosted the development of matter-wave optics. More recently the discovery of Bose-Einstein condensation has heralded the new field of atom lasers, one that promises more exciting developments as the range of systems and degree of control over them increases.