Bursting balloons is good fun, but there is also some fascinating physics lurking in how the fabric of the balloon is ripped apart. Two physicists in France have studied the bursting process using a high-speed camera, and have discovered that there is a critical point in the inflation of a balloon beyond which it will create beautiful flower-like patterns when it bursts. The research could boost our understanding of how materials fail when subjected to high degrees of stress.
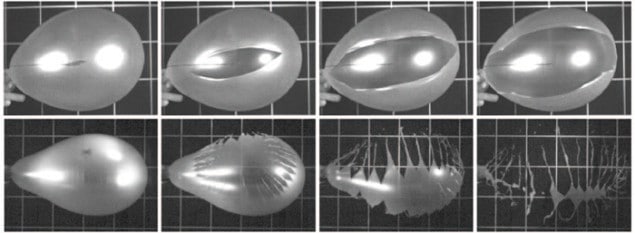
The French artist Jacques Honvault is famous for his high-speed photographic images, including a spectacular shot of a balloon fragmenting just after it is popped. This flower-like image fascinated the physicist Sébastien Moulinet of the École Normale Supérieure in Paris, because the fragmentation pattern is very similar to the patterns of cracks that can form when a material such as glass is struck by a hammer.
Blowing bubbles
To try to understand why these patterns occur, Moulinet and Mokhtar Adda-Bedia made balloons by forcing air into a latex membrane that is stretched over a circular aperture – a process akin to blowing a soap bubble. They then filmed the rupturing process at 60,000 frames per second using a high-speed camera (see video and image).
In some of their experimental runs, the balloons were filled to a relatively low internal air pressure and then pierced with the tip of a scalpel. In these cases, the slit made by the blade simply expanded as the balloon burst, leaving a piece of latex with just one slit in it.
Y-shaped cracks
Things changed dramatically, however, when the balloons were inflated to (or near to) the pressure at which they would burst spontaneously. In these cases the initial slit began to expand but then would suddenly split into two cracks that move off at angles to create a “Y” shape. These cracks would then undergo a similar division, and the process continued until the balloon was shredded into a number of finger-like pieces.
To understand the bursting process, the researchers looked at balloons made of latex of four different thicknesses and also varied the degree to which the balloons were inflated – the latter being related to the tension in the latex membranes. They found that the crucial parameter is the stress within the material – the ratio of the tension to the thickness of the latex. When the stress is above a critical value of about 1.8 MPa, the balloon will fragment. Below this critical value, the balloon will come apart in a single slit.
Speed of sound
Moulinet and Adda-Bedia believe that at low stress values the crack moves relatively slowly through the material, relieving stress as it goes. Higher stress values, however, correspond to faster crack-propagation speeds. The physicists believe that the critical stress value corresponds to the crack moving at its maximum speed. This was measured to be about 570 m/s, which the two physicists say is probably the speed of sound in the latex membranes. Because the crack can move no faster, the stress is relieved by creating two cracks.
Moulinet told physicsworld.com that he was “happy and amazed to be able to reproduce Honvault’s bursting balloon in the lab”. He also points out that the study could help scientists to understand how materials fail under stress. Moulinet and Adda-Bedia are now taking a closer look at how the cracks divide, and in particular the angles between the cracks.
The study is described in Physical Review Letters.