Researchers at Google Quantum AI have made an important breakthrough in the development of quantum error correction, a technique that is considered essential for building large-scale quantum computers that can solve practical problems. The team showed that computational error rates can be reduced by increasing the number of quantum bits (qubits) used to perform quantum error correction. This result is an important step towards creating fault-tolerant quantum computers.
Quantum computers hold the promise of revolutionizing how we solve some complex problems. But this can only happen if many qubits can be integrated into a single device. This is a formidable challenge because qubits are very delicate and the quantum information they hold can easily be destroyed – leading to errors in quantum computations.
Classical computers also suffer from the occasional failure of their data bits and error-correction techniques are used to keep computations going. This is done by copying the data held by a sequence of bits, so it is easy to spot when one of the bits in that sequence fails. However, quantum information cannot be copied and therefore quantum computers cannot be corrected in the same way.
Logical bits
Instead, a quantum error-correction scheme must be used. This usually involves encoding a bit of quantum information into an ensemble of qubits that act together as a single “logical qubit”. One such technique is the surface code, whereby a bit of quantum information is encoded into an array of qubits.
While this can be effective, adding extra qubits to the system adds extra sources of error and it had not been clear whether increasing the number of qubits in an error correction scheme would lead to an overall reduction in errors – a highly desired effect called scaling.
For practical large-scale quantum computing, physicists believe that an error rate of about one in a million is needed. However, today’s error correction technology can only achieve error rates of about one in a thousand, so significant improvement is required – which is a big challenge.
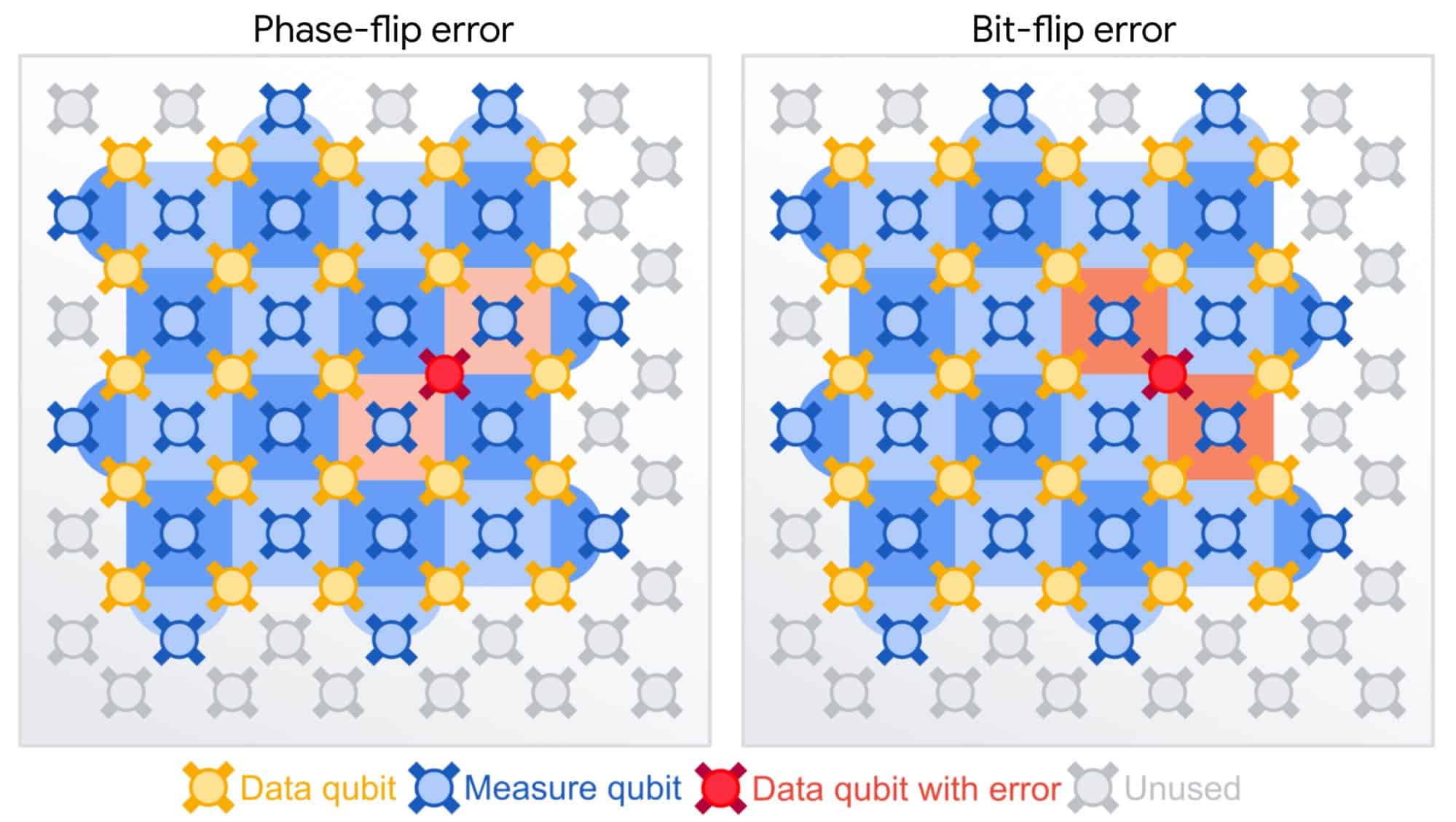
Bit flip and phase flip
Now, researchers at Google Quantum AI have taken an important step forward by creating a surface code scheme that should scale to the required error rate. Their quantum processor consists of superconducting qubits that make up either data qubits for operation or measurement qubits that are adjacent to the data qubits and can either measure a bit flip or a phase flip – two types of error that affect qubits.
The team then undertook a series of improvements to this basic design to boost its ability to deal with errors. The researchers used advanced fabrication methods to reduce error rates in individual qubits, including an increase in their dephasing lifetime. They also improved operational protocols, such as performing fast, repetitive measurements and leakage reset – where leakage refers to the unwanted transition of a qubit into a quantum state that is not used in computations.
Resetting leakage states
Error correction requires repeatedly retrieving intermediate measurement results in each error-correction cycle. These measurements must have low errors themselves so that the system can detect where errors on data qubits have occurred. The measurements must also be fast to minimize decoherence error across the qubit array. Decoherence is a process whereby the quantum nature of qubits deteriorates over time. Additionally, leakage states must be reset.
The team implemented a process called dynamic decoupling, which allows for both qubit measurement as well as the isolation that is needed to avoid destructive crosstalk between qubits. Here the qubits are pulsed to maintain entanglement and to minimize a qubit’s interaction with its measured neighbours. The advanced protocol also puts a number on the maximally allowed crosstalk interactions between qubits. Crosstalk introduces correlated errors that can confuse the code.
When running the experiment, the results must be interpreted to determine where errors have occurred, without full knowledge of the system. This was done using decoders that have access to more detail about their specific device to make better predictions of where errors occurred.
More means less
The researchers assessed that scalability of their design by comparing a “distance-3 array” logical qubit that comprised a total of 17 physical qubits with a “distance-5 array” that comprised 49 qubits. They showed that their distance-5 qubit array had an error rate of 2.914% and outperformed the distance-3 qubit array, which had an error rate of 3.028%. Achieving this reduction by increasing the size of a qubit array is an important achievement and it shows that increasing the number of qubits is a viable path to fault tolerant quantum computing. This scalability suggests that an error rate better than one in one million could be achieved using a distance-17 qubit array that comprises 577 qubits of suitably high quality. The team also looked at a 1D error correction code, which only focuses on only one type of error – bit or phase flip. They found that a 49-bit scheme can achieve error rates of around one in one million.
Can we use quantum computers to make music?
Julian Kelly, director of quantum hardware at Google Quantum AI, calls this result “absolutely critical” for scaling towards a large-scale quantum computer, adding that this experiment is a necessary gauntlet that every hardware platform and organization will need to pass through to scale their systems.
He says that the team’s next steps are to build an even larger and highly robust logical qubit that is well below the threshold for error correction. “The goal is to demonstrate algorithmically relevant logical error rates at a scale well beyond the systems that exist today. With this, we will cement that error correction is not only possible, but practical and lights a clear path towards building large-scale quantum computers,” he tells Physics World.
Hideo Kosaka, a quantum engineer at Japan’s Yokohama National University and who was not involved in this research, says that the surface code is considered the best practical method for scaling the number of qubits in a quantum processor since it allows a simple structure in 2D. Although he mentions that it is limited to a class of errors called Pauli errors, it would be enough in practice with possible future improvements of the device including shielding from cosmic ray impacts. Even though Kosaka thinks that this is just a starting point, where the researchers must improve their performance much more to reduce the number of physical qubits and error correction cycles, he does state that “no-one believed this would be realized within 20 years when we started research on quantum information science”.
The research is described in Nature.




