Overfishing is a worldwide problem and many of the world’s fish stocks are severely depleted. A fundamental question in light of the current state of affairs is whether it is at all possible to manage fishing grounds so that they remain sustainable? If so, how can the sustainability of fish stocks be best achieved and ensured? Surprisingly, perhaps, techniques from mathematics and physics are being used to answer these questions.

The primary cause of overfishing, and the consequent impoverished state of many fish stocks, is not due to poor science. Rather, it is due to economic and sociological factors. However, fisheries scientists sometimes “get it wrong”. Recent cases in point are the collapse of the cod stock off Newfoundland in 1990 and in the Barents Sea in 1999. Furthermore, lack of knowledge and understanding of the ecosystem and the dynamics of stocks make it harder for fisheries scientists to advise governments against the increasing exploitation of the world’s fish stocks.

Better understanding and improvements to the theories and models of the processes governing the dynamics of marine ecosystems are needed, and this is where physics and mathematics can help. Marine ecosystems are prime examples of large complex systems, and such systems are studied extensively throughout physics (Physics World December 1999 p57). However, unlike physics there are no clear “laws” in ecology, only general considerations, such as “big fish eat small fish”. The existing models therefore tend to be conceptual (see, for example, K G Magnússon 1999 J. Marine Research Institute (Reykjavik) 16 295-305).

Marine ecosystems are also extremely complex, so it is usually difficult to isolate cause and effect. For example, it is difficult to demonstrate the effects of biological interactions between species, due to the confounding effect of the physical environment. In addition, experiments are usually not feasible: the risk and/or the economic stakes are too high to justify experimenting with an ecological resource. Therefore it is not possible to test theories directly. However, “unintentional” experiments, such as the accidental depletion of a fish stock, can give useful information.

Moreover, direct measurements of the important variables, such as the biomass, are seldom possible. The number of fish cannot be counted directly, and instead has to be estimated using mathematical models of stock dynamics together with data, such as the age distribution of the catch, trends in catch rates and so on.

The tasks in fish ecology and fisheries can be divided into several closely connected parts. First we need to understand and model the processes that govern the dynamics of biological populations, including internal dynamics, and inter-species effects such as predator-prey interactions and competition for food. Next we have to develop mathematical models and statistical techniques that allow us to estimate the abundance and changing density of fish stocks, and predict future trends in a probabilistic manner. We then have to advise the relevant authorities on how many fish can safely be caught without jeopardizing future yields or, as is becoming increasingly important, adversely affecting specific components of the ecosystem. Ideally, this means presenting a range of options together with the likely consequences and a measure of the risks involved with each option.

Complexity and cod

The main driving force in the dynamics of fish populations is “recruitment”, which is usually defined as the number of fish reaching a certain age or size at which they are large enough to be caught by fishing fleets. Recruitment depends on a number of factors, such as the size of the spawning stock and environmental conditions. Understanding the processes that influence recruitment is perhaps the most important task in researching fish ecology.

Let us consider a familiar species, the Atlantic cod. Each female can produce millions of eggs that hatch into larvae, which drift with the currents. These larvae become juveniles, and three or four years later the fish are large enough to be recruited to the “fishable” part of the stock. By that time, however, their numbers are reduced to less than 1% of what they were at the time of hatching. Understanding what takes place from the time of spawning to the time the fish are recruited is a fundamental task in fisheries research.

A multitude of factors come into play: physical environmental conditions such as the temperature, salinity and turbulence of the sea are important, as is the availability of food for the larvae and juvenile fish. Cannibalism and predation on larvae and juveniles can also play a large part. So far it has been difficult to find models of recruitment that have sufficient explanatory and predictive power.

Many of the same biological and environmental factors affect older fish as well. The rates with which the fish are eaten by predators are relatively easy to observe and have been quantified, modelled and simulated. Meanwhile, food-consumption rates and the resulting growth rates of individual fish have also been modelled, although empirical verification has been elusive. Attempts have also been made to model migrations and spatial structure in fish stocks, but this work is still at an early stage.

Apart from recruitment, fishing operations – the resulting catch rates and the mortality rates caused by fishing – are the single most important factor affecting the dynamics and stock sizes. A great deal of work has been carried out to describe this process and predict the effects of various types of management rules for regulating fishing at sea. Other processes that must be considered include natural mortality rates, maturation (and what determines it), competition and density dependence.

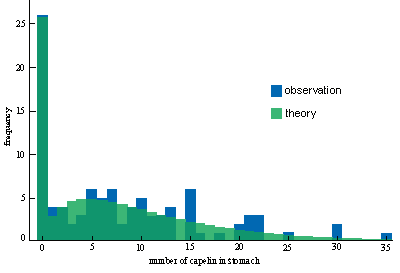
All of the processes governing the dynamics of ecosystems are random. Ideally, the models developed to describe them should be stochastic, and give results and predictions in terms of probability distributions. The theory of stochastic processes – which is widely used throughout physics – has thus been used to model and analyse the changes in population sizes. Species interactions such as predation have also been modelled this way (see figure).

However, due to the complexity of ecosystems, deterministic models are frequently used as a first approximation. Such models can provide useful qualitative information, for example on the stability and oscillations in populations, and on the direction of changes that result from certain actions. Nevertheless, the fact remains that because of the large random element in ecosystem dynamics, some degree of uncertainty is inherent in all estimations of the state of fish stocks and in all predictions. This is due to noisy observations as well as the stochastic nature of the dynamics.

Fisheries science and fisheries management must therefore learn to deal with this by attempting to quantify and model the uncertainty, and by managing fisheries with this in mind. The greater the uncertainty, the more cautious the management policy must be.

New approaches to fishing

The methods of statistical physics and stochastic geometry may prove to be useful in understanding and modelling the recruitment process. Initially, the eggs and larvae are like particles drifting in space. Therefore, when modelling their distribution and density, the interactions with other “particles” – such as food particles, other larvae competing for food, and predator “particles” – suggest the use of methods from statistical physics. These methods can be used to derive the probability distribution of the various particle types in a given region of space, the distribution of inter-particle distance, the contact rates between predator particles and prey particles, and so on.

Indeed, stochastic geometry has already been applied to the ecology of plankton (see B Rothschild 1992 Phil. Trans. R. Soc. London B336 225-237). The next step is to apply these methods to the ecology of eggs and larvae, thereby potentially improving the understanding of the recruitment process.

Statistical physics may also have a role to play in understanding the dynamics of fish schools (E Bonabeau and L Dagorn 1995 Phys. Rev. E51 R5220-R5223). Physical models of particle aggregations can be used to model such phenomena as the aggregation and splitting up of fish schools, and studies have demonstrated that the size distributions of fish schools may be governed by power laws. Better understanding and improved models of the dynamics of fish schools, their migrations, and the factors governing the spatial distribution of fish, are of crucial importance in fish ecology. As yet, however, this remains essentially an unsolved problem.

The relatively recently discovered phenomenon of stochastic resonance may also be relevant in fish-population dynamics. This effect can occur when noise is superimposed on a weak periodic signal, which would otherwise not be detectable, and this noise leads to large amplitude fluctuations. Stochastic resonance has been observed in a large variety of systems in nonlinear optics, condensed matter and biophysics (L Gammaitoni et al. 1998 Rev. Mod. Phys. 70 223-287). It has been hypothesized that the recurring outbursts and collapses in some fish stocks are a stochastic-resonance phenomenon where environmental noise is superimposed on a weak predator-prey signal, or some other deterministic oscillatory signal.

The methods of applied mathematics and physics are indispensable in the studies of fish ecology and fisheries. Although a large number of unsolved issues remain, there is no doubt that mathematics and physics may lead to a better understanding of marine ecology and help us to protect our fragile environment.