Nearly a century after Einstein predicted the existence of gravitational waves, the long effort to detect them directly is heating up. David Appell explains how a major upgrade at the Laser Interferometry Gravitational-wave Observatory may soon bring the hunt to a successful close

In the dry scrubland of eastern Washington State, a few miles from what was once America’s premier plutonium factory, sits a massive laboratory, its two long arms stretching off into the distance. On windy days, tumbleweeds roll by, piling up against the arms’ concrete housing and creating headaches for the lab’s maintenance workers. Inside, though, there is a buzz of activity as scientists at the Laser Interferometer Gravitational-Wave Observatory (LIGO) prepare for the most exciting period in the facility’s 14-year history. Later this month, they will begin observations with an upgraded machine, new instruments and a corresponding sense that this time, when they go on a gravitational-wave hunt, they’re going to catch a big one.
Gravitational waves were predicted by Albert Einstein in 1916 as a consequence of the field equations of his general theory of relativity. These 10 coupled nonlinear equations formulate the universe as the dynamic interplay between mass–energy and space–time. As the physicist John Wheeler put it, “Matter tells space how to curve, and space tells matter how to move.” One prediction of the general theory is that when massive bodies move around, they cause the fabric of space–time to warp, generating ripples that propagate outwards at the speed of light. These ripples are known as gravitational waves, but they are not the familiar sinusoids found in electromagnetism. Instead, they stretch space in one direction perpendicular to the line of travel, while simultaneously compressing it in the other – a bit like lips puckering up and down for a kiss.
No prediction made by Einstein’s equations has ever been proved wrong, and in the 1970s observations of a binary pulsar – a rapidly rotating neutron star in orbit around another neutron star – strongly suggested that gravitational waves do indeed exist (see “Pulsar detectives” below). However, nobody has ever detected such waves directly, despite decades of trying.
LIGO was built to change that. From 2002 until 2010, laser beams travelled from the lab’s hub down its two long, perpendicular arms, where they reflected off huge, hanging masses and were recombined back near their origin. The idea was that a passing gravitational wave would cause the masses to move enough for the length of the arms to change and produce a detectable phase shift in the interference pattern of the recombined laser beams. On a handful of occasions during LIGO’s first period of experimental operations, researchers thought they had spotted such a shift – only for the supposed signal to be revealed as noise or, in one case, a deliberate fake generated by researchers within the collaboration, as a test of their internal data-checking procedures.
Now, however, the LIGO facility near Hanford, Washington – along with its twin in Livingston, Louisiana – is entering a new era. In March contractors completed a $221m upgrade of the dual facilities that improved their ability to detect the feeble waves of gravity by a factor of 10. Thanks to this upgrade – known as Advanced LIGO, or aLIGO – researchers should be able to detect gravitational waves that originate anywhere within a sphere of about 420 million light-years in radius, centred on the Earth. That is still only a small fraction of the total universe, but it’s a thousand-fold increase (by volume) on what was possible before the upgrade. As the upgraded system kicks into high gear and achieves its designed sensitivity in 2016 or 2017, the scientists at LIGO are quietly confident that they will see something real.
Only an attometre
The recently completed aLIGO upgrades all have the same goal: reducing noise. Noise poses challenges for many physics experiments, of course, but for the dual LIGO machines and their interferometric kin, the problem is particularly acute. Although gravitational waves come from some of the most massive and energetic systems in the universe (such as a pair of black holes or neutron stars orbiting one another) their amplitudes are exceedingly small by the time they reach Earth. In fact, a passing gravitational wave is expected to change the length of LIGO’s 4 km-long arms by only a few attometres (10–18 m) – around 1000 times less than the diameter of a proton (see “How LIGO works” below).
To ensure that the observatory can detect such a tiny change, almost every aspect of LIGO has been upgraded. For starters, a new isolation system has been installed to keep seismic noise (caused, for example, by passing trucks or tiny earthquakes) negligible across the range of frequencies that interest would-be wave observers. The dual US facilities are vital here, since noise seen in one facility but not the other can be ruled a local hiccup, not a passing gravitational wave.

At higher frequencies, though, the performance of the LIGO detector is limited by shot noise, which arises from the quantum nature of light. Basically, the number of photons produced by the laser fluctuates with time, creating a degree of uncertainty in the amplitude and phase of the beam. Increasing the laser’s power mitigates this problem somewhat, because the signal produced by a passing gravitational wave varies in proportion to the power, while the shot noise is proportional to the square root of the power. Accordingly, aLIGO boosts the power of the facility’s laser by more than an order of magnitude, from an initial input of 10 W to about 200 W.
That, however, creates a new problem. Each of those laser photons packs a tiny momentum punch and, collectively, they generate enough radiation pressure to make the masses at the end of each arm twitch ever so slightly. To counteract this, the masses have been beefed up: the aLIGO masses are both larger in diameter (34 cm instead of 25 cm) and more massive (40 kg instead of 11 kg) than before. That reduces their radiation-pressure-induced motion down to a level comparable to the thermal noise in the wire that suspends them – noise that has itself been reduced by replacing the old steel wire with fused silica fibres.
Putting the squeeze on
To really get a handle on shot noise, though, you need ingenuity as well as more powerful lasers and bigger masses. This is where the expertise of physicists like Sheila Dwyer comes in. A postdoctoral researcher at LIGO’s Hanford site, Dwyer began working at the lab in 2010, when she was a PhD student at the Massachusetts Institute of Technology. Her graduate work (conducted with the astrophysicist and gravitational-wave detection specialist Nergis Mavalvala) spanned quantum optics, quantum measurement theory and gravitational-wave detection, and it prepared her to play a central role in one of the most important aLIGO upgrades: the switch to a laser that emits light in an exotic form called a “squeezed state”.
Like all particles, the photons in squeezed light obey the uncertainty principle: the product of the uncertainties in any two complementary properties (such as amplitude and phase) always equals or exceeds ℏ/2. What makes squeezed light special is that the uncertainty in one of these variables has been “squeezed” down, while the uncertainty in the other is correspondingly allowed to balloon upwards. At LIGO, the fluctuations in phase are squeezed, so that the phase shift of the recombined beam can be measured more precisely. Of course, this means that the fluctuations in the beam’s amplitude become relatively large – making it all the more important that the mirrored masses used in aLIGO be as heavy as is reasonably possible.
Dwyer explains that LIGO is not the first gravitational-wave interferometer to use squeezed light. That honour belongs to the GEO600 experiment in Sarstedt, Germany, which began working with squeezed light in 2011 and now uses squeezing in its normal operations. Physicists there found that at certain frequencies (around 3 kHz), squeezing reduced quantum noise by a third, increasing the machine’s detection rate of gravitational waves in that frequency band by a factor of (3/2)3 (about 3.4). For LIGO, Dwyer showed in her doctoral thesis that using squeezed light would increase detector sensitivity by 80%, leading to an improved detection rate of almost a factor of six.
Knowing what to look for
While experimentalists have focused on upgrading LIGO’s physical components, theorists have been improving their understanding of what a gravitational-wave signal might look like. To help identify a passing wave, numerical relativists have calculated the waveforms that several of the most likely sources of gravitational waves are expected to generate. Thanks to their efforts, any signal registered at LIGO can be compared with about 10,000 expected waveforms for gravitational waves created by binary neutron stars, around 100,000 created by binary black holes and on the order of a million waveforms from neutron-star–black-hole binaries. This last number is larger than the others because the black hole’s angular momentum can couple to the orbital angular momentum of the binary pair, producing a much more complicated waveform (see “Relativity’s new revolution“).
In addition to building the database of expected waveforms, some researchers have been developing algorithms that look for gravitational-wave signals from other, unimagined sources. This type of search (known as a “burst” search) does not make any assumptions about the waveforms it is looking for, explains Duncan Brown, a gravitational-wave astronomer at Syracuse University in New York. “That way, when the universe goes bump in the night, LIGO will feel it,” he adds.

Astronomers have also worked out how many events aLIGO might expect to see as it approaches its design sensitivity. Binary neutron stars are considered the most promising source of gravitational waves, and (based on observations made with conventional telescopes) researchers estimate that aLIGO could see up to three binary-star coalescences – events in which two stars merge to form a single body – in its first year of operations. In its second year, as further technical improvements expand the fraction of the universe being observed, it might see a further 20 coalescences, and perhaps as many as 200 after four years. But it could also see none at all. Although that would be a surprise, it is possible that noise could, despite the upgrades, drown out a gravitational-wave signal; that binary-star coalescences could occur less often than astronomers think they do; or even that the strong-field, nonlinear gravitational regime, where coalescences finish, lies beyond general relativity.
The collapse of a star’s core as it becomes a supernova would also generate gravitational waves, unless the collapse is spherically symmetric. However, the maximum amount of gravitational-wave energy expected in such an event is much smaller than from binary coalescences (by a factor of at least 107). This means that gravitational waves from a core collapse may be seen only if the collapse happens in our cosmic backyard: within the Milky Way or its smaller, satellite galaxies – the Large and Small Magellanic Clouds.
The era of ‘multimessenger astronomy’
Whatever its cosmic source, the first direct detection of a gravitational wave will be big news. It will confirm a prediction from general relativity, but more importantly it will also give astronomers, astrophysicists and gravity theorists entirely new information about the objects they study. Indeed, astrophysicists hope that gravitational-wave observatories will someday operate as routinely as optical telescopes do today. If that happens, gravitational waves could fundamentally alter our picture of the universe, just as radio-wave and X-ray astronomy altered it from the placid, silent galaxies Edwin Hubble observed at visible wavelengths to the raucous universe we know today, full of quasars and pulsars, black holes and neutron stars. At some point, it may even be possible to observe cosmic events such as supernovae with light-based telescopes, neutrino detectors and gravitational-wave observatories – a new type of science dubbed “multi-messenger astronomy”.
More prosaically, a detection at LIGO or another ground-based observatory could also pave the way for a more ambitious successor facility. Dwyer, the LIGO postdoc, is part of a small group working on plans for the next generation of detectors. An underground observatory with arms 40 km long could bring another factor of 10 in sensitivity, she says, and it could, in theory, detect gravitational waves generated a mere billion years after the Big Bang – corresponding to a region of space–time far bigger than aLIGO’s current sphere of sensitivity.
Still more ambitious are plans to put a gravitational-wave observatory in space. Designs for the European Space Agency’s eLISA project, for example, call for three satellites arranged in an “L” shape so that each “arm” – consisting of empty space – is 1 million km long. The separation distances would be monitored to detect gravitational waves at frequencies between 0.03 mHz – below which the spacecraft are buffeted by fluctuations in solar radiation pressure, solar wind and cosmic rays – and 100 mHz. Within this range, expected gravitational-wave sources include galactic short-period binary stars and supermassive black-hole binaries. Once gravitational-wave detection is routine on Earth, new ideas, even beyond eLISA, will surely abound. The sky – no, the universe – is the limit.
Pulsar detectives
The existence of gravitational waves was implied in a beautiful series of observations made more than 30 years ago by Joseph Taylor Jr and Joel Weisberg, utilizing a new type of pulsar discovered by Russell Hulse and Taylor in 1974. The pulsar PSR B1913+16 is a rapidly rotating neutron star that emits electromagnetic radiation, in orbit around a neutron star that was not seen to pulse. The general theory of relativity predicts that such a system will radiate energy, E, at a rate of
where m1 and m2 are the masses of the two bodies orbiting one another in circular orbits a distance r apart. (The calculation and expression for an elliptical orbit is a bit more complicated.) Note that the radiated power, P, is negative because the system is losing energy as the two masses spiral in towards one another.
For the Earth–Sun system, this energy loss rate comes to a feeble 200 W (less than used by a toaster), and a related calculation shows that the distance between them changes by only 400 fm (10–15 m) per year. But for a binary pulsar system such as PSR B1913+16, the rate of energy loss is almost 1025 W – equivalent to about 2% of our Sun’s output of electromagnetic radiation. By monitoring the system over several years, Taylor and Weisberg found that the stars’ separation was shrinking rapidly, by about 2 cm per day. More importantly, their observations showed that the cumulative shift of the stars’ orbital periastron (the point where the stars are closest together) decreased in a way that almost exactly followed the predictions made by general relativity. Subsequent work found an even tighter agreement.
Hulse and Taylor were jointly awarded the 1993 Nobel Prize for Physics for their discovery of the first binary pulsar. The Taylor and Weisberg result, more than anything, convinced physicists that gravitational waves exist.
How LIGO works
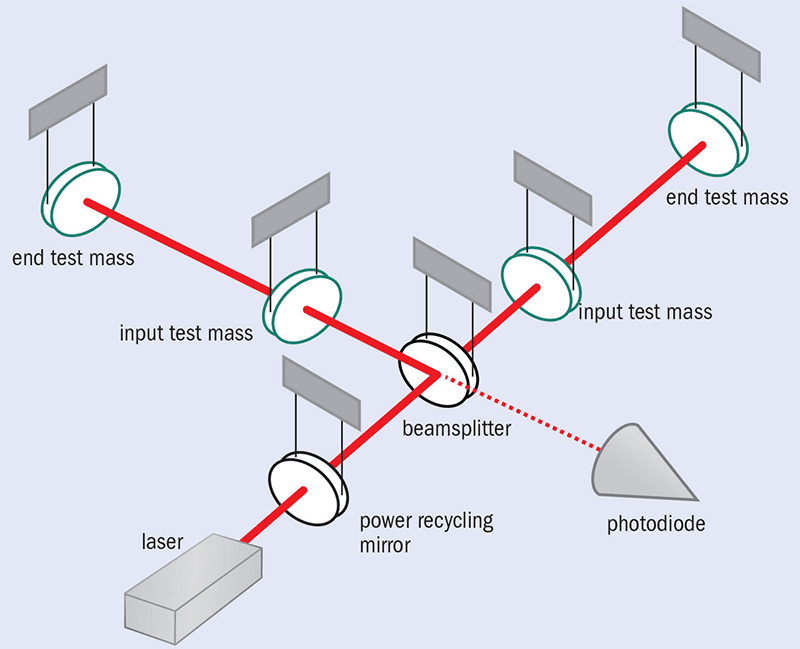
LIGO and other interferometric gravitational-wave observatories (such as VIRGO in Italy, GEO600 in Germany and KAGRA in Japan) consist of two long arms built at a right angle to each other. At the end of each arm hangs a highly polished “test mass” that acts as a mirror for a laser beam that is split at its source, with separate beams reflected down each arm. If a gravitational wave from a distant source washes through the detector, it will change the distance between space–time points in the detector ever so slightly, producing an alteration in the length of the interferometer’s arms.
The magnitude of this length change ΔL will be the arm length (4 km in LIGO’s case; 2 km for VIRGO and KAGRA; 600 m for GEO600) multiplied by a dimensionless strain factor h ∼ (GM/Dc2)(v2/c2), where M is the mass of the system generating the gravitational wave, v the characteristic velocity of the system’s components (such as two black holes orbiting one another) and D its distance from the detector. The value of h varies inversely with the distance of the source, but with the most likely sources – coalescences of binary stars in nearby galaxies and superclusters – h is expected to be of the order 10–21. Hence, to detect a gravitational wave, LIGO needs to be able to measure a change in the length of its arms of about 4 × 10–18 m.
To accomplish this remarkable feat, gravitational-wave astronomers rely on some sophisticated optics. In each of LIGO’s two arms, the beam is reflected up to 400 times in a Fabry–Perot cavity, travelling a total distance many times the facility’s arm length. The two beams are then recombined at a photodetector, which measures the phase difference of the two beams. The change in the light travel time for each beam will be Δt = 2(ΔL/c) = 2hBL/c, where B is the number of bounces, creating a phase shift ΔΦ = (2π)f Δt = 4πhBL/λ – about 10–9 radians, where f is the laser frequency and λ its wavelength.
In its initial phase, LIGO was designed to detect gravitational waves with frequencies from about 40 Hz to the highest gravitational-wave frequencies expected, 10,000 Hz, with its strain sensitivity lowest at about 100 Hz. The aLIGO upgrades improve on this by shifting the observatory’s lowest detectable frequency down to 10 Hz, and boosting its strain sensitivity by a factor of 10, to values of h below 10–22. (Below about 1 Hz, even small seismic vibrations and inhomogeneities in the Earth’s gravitational field from atmospheric fluctuations create insurmountable noise.) As LIGO scientist Rick Savage puts it, “We’re far beyond splitting hairs here.”



