Last summer, the neutron celebrated its 80th birthday. This was not, of course, the 80th anniversary of its birth, for the neutron is only about one second younger than the universe itself. Rather, the celebrations marked eight decades since James Chadwick published a paper announcing the discovery of an electrically neutral particle to sit alongside the previously discovered proton within the atomic nucleus.

Quite soon after Chadwick’s landmark discovery, scientists realized that this neutral particle held enormous potential as a tool for studying nature’s fundamental laws. Neutrons offer a complete laboratory for experimental physicists. They experience all four known fundamental forces – gravity, the electromagnetic force, the weak force responsible for radioactivity and the strong force that keeps the particles in atomic nuclei bound together – but crucially, they are electrically neutral and thus insensitive to the effects of electric fields. Neutrons are therefore excellent candidates for investigating how gravity operates at the microscopic scale and how it fits in with the weird and wonderful world of quantum mechanics.

However, the neutron’s greatest asset can also be a drawback in practical terms. Since they have no electric charge, neutrons can easily pass through substances or penetrate deeply into them. Indeed, this property is exploited in condensed-matter research and certain types of imaging. But it also means that – unlike beams of protons, such as those in the Large Hadron Collider (LHC) at CERN – neutrons cannot be guided or focused using electric fields, and in general they are difficult to isolate and “hold” for further study.

The solution – which was already being hinted at in the 1950s, though it would be more than a decade before it was put into practice – is to cool the neut­rons down to very low temperatures. Neutrons are officially “ultracold” at 2 mK above absolute zero. At such temperatures, their mean velocity is less than 6 m/s, so they can only travel about 2 m upward against the pull of the Earth’s gravity. They are also totally reflected from certain materials, such as copper or stainless steel, at any angle of incidence. This is useful as it makes it possible to store and observe ultracold neut­rons for a relatively long time, and thus to make very high-precision measurements of their properties.

The effects of new particles or forces may show up in the static and decay properties of the neutron

Today, a growing community of scientists at my institution, the Institut Laue-Langevin (ILL) in Grenoble, France, and other facilities around the world are using ultracold neutrons to test aspects of the Standard Model of particle physics. Like our high-energy counterparts at the LHC, our goal is to find evidence of “new physics” beyond the Standard Model – which, despite its tremendous success, cannot explain or predict some of the most basic, yet unanswered, questions in physics, such as why the elementary particles have the masses that they do, and why the universe evolved to have more matter than antimatter. However, ultracold-neutron researchers go about this task in a very different way. In an accelerator, the energies of the colliding particles are often high enough to reproduce temperatures, densities and conditions not seen since shortly after the Big Bang. In contrast, ultracold-neutron research takes place at much lower energies, so we do not actually produce new particles that can be directly observed in a specialized particle detector. However, theory predicts that the effects of new particles or forces may show up in the static and decay properties of the neutron. Careful study of these properties therefore enables us to test predictions from the Standard Model and look for new physics beyond it.

Early experiments

The identity of the first person to observe ultracold neutrons is a minor Cold War mystery, one of several that arose as a result of frequent obstructions to the free flow of information from East to West (and vice versa). On the Soviet side, Yakov Borisovich Zel’dovich made an important theoretical advance in 1959, when he published a paper proposing a method of storing neutrons at low temperatures and also made the first predictions of the properties of ultracold neutrons and what they could be used for. Despite this, it was not until nearly 10 years later that his countryman, Fedor L’vovich Shapiro, succeeded in extracting them from a reactor at the Joint Institute for Nuclear Research (JINR) in Dubna, Russia.

For their neutron source, Shapiro and his team used the JINR’s pulsed reactor. After slowing down, or “moderating”, the fission neutrons with paraffin, the resulting population of slower – but still warm, or “thermal” – neutrons was then sent through a curved guide system that was designed with several sharp turns in the horizontal plane. These neutrons could not travel the whole length of the guide without striking the guide wall. Only neutrons in the very-low-energy “tail” of the Maxwellian distribution of thermal neutrons were reflected, rather than absorbed, when they collided with the guide walls, and were thus able to reach the detector at the other end. The flux of ultracold neut­rons in the extracted beam at Dubna was only about two or three neutrons per 1000 seconds, but despite this obstacle Shapiro pressed ahead, convinced that slow-moving neutrons could help answer some of the fundamental questions in physics. In the summer of 1968, he and his colleagues successfully defied cynicism from their peers by observing these tiny cold particles and proving they could be stored for several seconds.

At around the same time, on the other side of the Iron Curtain, ultracold neutrons were also being extracted from the research reactor at the Technische Universität München in Germany. Albert Steyerl was working on research of a more applied nature, investigating the scattering of low-energy neutrons in different materials as a function of their velocity. He selected neutrons from a secondary graphite moderator and used the Earth’s gravitational field to slow them down, sending the neutron beam vertically through an 11 m long curved tube. Some of the neutrons that emerged at the top end of the tube had lost so much energy that they had become ultracold, and Steyerl was able to confirm this by measuring their velocities.

Regardless of which group came first, what is certain is that following these initial breakthroughs, the 1970s and 1980s saw a number of institutes in both East and West set up their own ultracold-neut­ron “factories”. However, the highest achievable densities of stored neutrons were still relatively low, typically 0.1 per 1 cm³, which limited the measurements that could be performed. As a result, scientists started to investigate other techniques for producing cold neut­rons, such as cooling down the neutron spectrum within the reactor itself. This strategy increased the proportion of neutrons with velocities low enough for them to be stored for further study.

The technique adopted at the ILL in 1985 begins with energetic fission neutrons produced in the institute’s high-flux reactor. These neutrons are moderated by heavy-water molecules in the tank that contains the reactor core. Inside this tank is a second moderator full of liquid deuterium at 25 K. As the thermal neutrons pass through this second moderator, they lose energy by colliding with the cold deuterium nuclei and emerge with average velocities of around 700 m/s. As in Steyerl’s early experiments, the neutrons are then sent upwards through a guide, slowing down further under the influence of gravity. The neutrons emerge at the top of the pipe with average speeds of about 50 m/s and are then sent into a large vacuum vessel. This vessel contains a turbine with metal blades that rotate backwards when the neutrons hit them (a design first proposed and implemented by Steyerl in 1976). This back-rotation “cushions” the neutrons and causes them to lose some of their kinetic energy. The basic principle is similar to pulling back your tennis racket just as the ball hits it; in technical terms, the neutron gets Doppler shifted from a velocity of about 50 m/s down to about 5 m/s.

As well as being highly effective, the turbine’s mechanical mechanism provides researchers with a very reliable, constant-intensity source of ultracold neutrons. This has proven to be a major benefit to scientists working on high-precision measurements, as the flux of ultracold neutrons and the storage densities achievable with this system are about 50 times higher than was previously possible. As a result, the ultracold neutrons produced at the ILL have been the foundation of some of the longest-running and most important experiments in this field.

The fall of a neutron

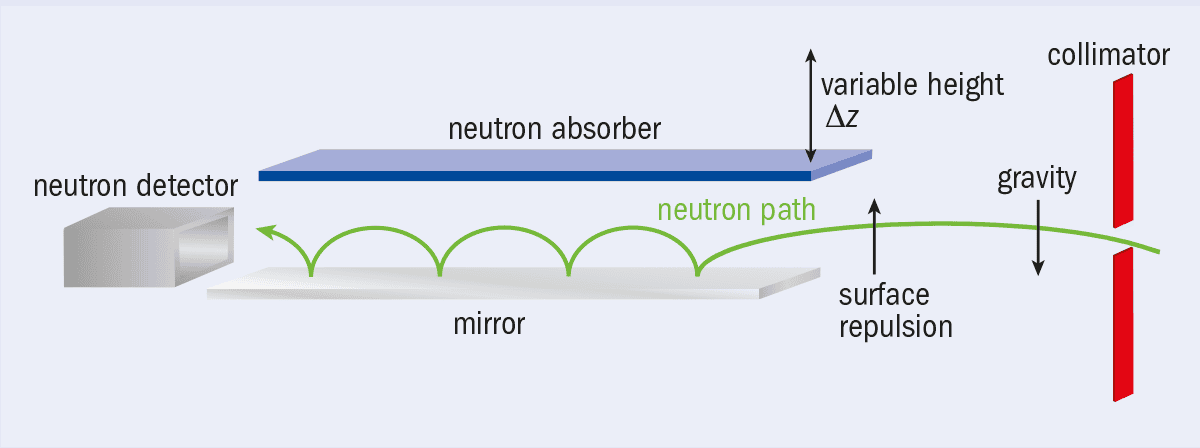
One of the experiments performed using the ILL’s turbine system involved “bouncing” ultracold neut­rons along a mirror to see how they behave under the influence of gravity. In this experiment (V Nesvizhevsky et al. 2002 Nature 415 297), neutrons leaving the turbine were directed through a slit composed of two parallel plates, each about 10 cm long and separated by a distance Δz that could be varied by a few tens of microns (figure 1). The upper plate had a rough surface that absorbed any neutrons that collided with it, while a lower plate made of standard optical polished glass reflected neutrons like a mirror. The combination of the mirror and the Earth’s gravitational field formed a potential well: a neutron falling towards the mirror would interfere with its own reflected wave, and this self-interference created a standing wave in the neutron density along the vertical direction.

One would normally expect the neutron transmission rate T to be proportional to Δz^1.5 (the additional power of 0.5 is down to the fact that increasing Δz allows neutrons with a greater spread of vertical velocities to enter the system, as well as improving their chances of being transmitted through it). Instead, the researchers saw T rise sharply from a negligible background level as soon as they increased Δz above 15 μm – the height at which the spatial wavefunction of neutrons in the ground state began to “fit” between the two plates. This study marked the first time that quantum states of matter had been observed in a gravitational field, and it opened the door to more complex experiments. For example, in 2011 a research team from the Vienna University of Technology and the ILL modified the parallel-plate arrangement so that the mirrored plate could be vibrated at particular frequencies, boosting the neut­rons into higher quantum energy states (T Jenke et al. Nature Phys. 7 468).

The next step will be to measure very precisely the energy differences between the various quantum states of a neutron in the Earth’s gravitational field. Such measurements are important because they provide a means of testing Newton’s theory of gravity at length scales of a few microns or millimetres. Any deviations from predicted values could reveal the existence of a new, short-range “fifth force” that couples to the neutron via some as-yet-undiscovered force-mediating boson. Conversely, if such deviations are not observed, that would place limits on the strength of the hypothetical fifth force and constrain theories of physics, such as string theory or extra dimensions, that incorporate such a force.

Here today, gone…when?

Although neutrons remain stable for billions of years within the atomic nucleus, free neutrons decay into protons, electrons and electron antineutrinos after a little less than 15 minutes. But the neutron lifetime is not known with great accuracy, and the accepted value for it has changed several times as experiments became more precise. Even after 60 years of experiments, there remains about a second’s worth of uncertainty in the current figure. Finding a more precise value for the neutron’s lifetime would be tremendous as it could help to answer a number of fundamental questions in physics.

Finding a more precise value for the neutron’s lifetime would be tremendous as it could help to answer a number of fundamental questions in physics

The first of these questions concerns the synthesis of nuclei in the aftermath of the Big Bang and the make-up of the matter that formed in the first few minutes of the universe. We know that during this period, protons and neutrons came together to form the first light elements, which in turn became the raw material for the first stars. We also know that the most common element formed was hydrogen, followed by a much smaller amount of helium and traces of lithium. However, the exact ratios of these elements actually depend to a large extent on the lifetime of the neutron. Had that lifetime been much smaller than it is, the universe would consist almost entirely of hydrogen; much larger, and it would contain only helium. The neutron’s true lifetime must be somewhere between these two extremes, and being able to pin down its value more precisely would allow us to test theories of the early universe.

As well as helping us to understand the make-up of “normal” matter in the early universe, knowing the precise lifetime of the neutron would also help scientists make more accurate predictions of the total amount of matter created. This, in turn, might reveal how much dark matter must exist to make our theories of the universe’s evolution consistent. Finally, a better knowledge of the neutron’s lifetime could provide insight into the operation of the weak force, since the decay of free neutrons is based purely on weak interactions. Precise measurements of the neutron’s lifetime can tell us much about the strength and structure of this force, which also governs nuclear fusion reactions, such as those that take place within stars.

Experiments that aim to improve the accuracy of the lifetime measurement can be grouped into two categories, known as “counting the dead” and “counting the survivors” (F E Wietfeldt and G L Greene 2001 Rev. Mod. Phys. 83 1173). The first type of experiment uses a beam of neutrons that are counted as they pass through a detector. After the beam has travelled some distance, a second detector measures how many protons or other decay products (“dead neut­rons”) are left behind. With experiments of this type, such as the one at the National Institute of Standards and Technology (NIST) in Maryland, US, the principal challenges are correctly counting the “live” neutrons entering the beam and then ensuring that all of the neutron decay products in the beam path are detected and accounted for. Several techniques, such as beam guides and new types of detectors, have been developed to improve this counting accuracy.

The second type of experiment uses neutrons that are stored in a container coated with a neutron-reflecting material, or in a magnetic “bottle” that traps neutrons using their sensitivity to magnetic fields. After neutrons are loaded into the container and a certain number of seconds have passed, the “surviving” neutrons are counted and the neutron bottle is emptied. This measurement is then repeated for several different storage times in order to trace out an exponential decay curve from which the neut­ron’s lifetime can be calculated.

In stored-neutron experiments, the absolute number of neutrons remaining after a particular time is not important. Instead, what matters is how this number changes as storage times are increased. Hence, stored-neutron experiments, such as the one currently operating at the ILL, are less sensitive to detector inefficiencies than is the case for beam-type experiments. However, they are sensitive to leakages caused by the scattering or absorption of neutrons in the storage container. Such leakages are one reason why magnetic bottles are being developed to replace forms of storage that allow the neutrons to bounce off the container walls like ping-pong balls.

Broken symmetries

Although the neutron appears electrically neutral overall, it is composed of up and down quarks, which carry opposing fractional electric charges. If the average positions of these charges within the neutron did not coincide, the neutron would have an electric dipole moment (EDM) and would be affected by an electric field. The existence of a neutron EDM would directly violate symmetries of nature (figure 2) related to parity (P) and time (T). To get a physically intuitive picture of why this is so, imagine the neutron (which has a nuclear spin) as a spinning top. If you take a symmetrical top, flip it upside down and watch a time-reversed film of it precessing as it spins on its axis, it will look the same as it did before these transformations took place. But if the top is not symmetrical – if, in this analogy, the neutron has an EDM – you will be able to tell the two systems apart, so P and T symmetries must be violated.

The violation of T symmetry implies that a neutron EDM would also violate the combined charge–parity (CP) symmetry. The reason for linking the two is that there is no physical process that simultaneously disobeys charge, parity and time (CPT) symmetry; as far as we know, all physical laws would remain the same if the electric charges and spatial coordinates of all the particles in the universe were inverted and time went into reverse. Hence, either both CP and T symmetries must be violated, or neither of them. Examples of CP violation are of great interest to physicists because most explanations for why our universe is full of matter, and not antimatter, rely on a significant degree of CP violation taking place just after the Big Bang. And while there are several experimentally verified examples of CP violation in processes associated with the weak force, these do not contribute enough to explain the matter–antimatter imbalance we now observe. This is one of the significant shortcomings of the Standard Model – it does not include a sufficient degree of CP violation.

The idea that the neutron might have a non-zero EDM was first proposed by Norman Ramsey and Edward Purcell in 1950 and the first experiments (using thermal neutrons) to put an upper limit on the EDM’s magnitude were conducted at the Oak Ridge National Laboratory in Tennessee, US, a year later. Subsequent experiments using ultracold neutrons have lowered this limit, but searching for a neutron EDM is by no means an easy task. To give you an idea of the challenge the neutron-science community faces in trying to measure it, imagine blowing a neutron up to the size of the Earth. On this scale, the current limit on the maximum size of the neutron EDM would correspond to a separation between positive and negative charge centres of less than 3 μm – about the width of a hair – within the centre of the Earth (C A Baker et al. 2006 Phys. Rev. Lett. 97 131801).

However, some theories that go beyond the Standard Model (and that might resolve the issue of why the universe is composed of more matter than antimatter) predict a neutron EDM somewhat smaller than this, so neutron researchers are developing even more sensitive experiments to measure it. The experiments taking place at the ILL begin by loading a spin-polarized sample of ultracold neutrons into a storage bottle. A very stable, homogeneous and well-controlled magnetic field is then applied to the system, and as the neutron spins precess around the field’s axis (similar to the principle upon which magnetic resonance imaging, or MRI, is based) their Larmor precession frequency is measured. Next, a very strong electric field is applied in a direction that is either parallel or anti-parallel to the magnetic field. If the neutron has an electric dipole moment, it will “detect” whether the electric and magnetic fields are parallel or anti-parallel, and its spin precession frequencies will be different in the two cases.

More neutrons, more science

The sensitivity of this frequency-difference measurement depends on three factors: the strength of the applied electric field; the storage time; and the number of neutrons in the apparatus. It is difficult to increase the field because of the need to avoid charge breakdown. As for the storage time, it cannot be higher than the 880 s lifetime of a free neutron – though in practice, leakages reduce the storage lifetime to around 250 s. Physicists are therefore looking for new materials that offer a higher charge-breakdown threshold and longer storage times. However, perhaps the most promising strategy for improving the sensitivity of the neutron EDM measurement is instead to increase the number of neutrons we can store. This approach is also true for other types of measurements on ultracold neutrons (and, generally, all particle-physics experiments): the more particles you have, the more precise the results you can obtain.

Consequently, groups around the world are developing a new generation of sources that should deliver higher densities of stored neutrons and open up new avenues for research. At present, new sources are either planned, under construction or have recently gone into service at facilities in Canada (TRIUMF), Germany (Technische Universität München, Johannes Gutenberg University Mainz), Japan (J-PARC, Research Center for Nuclear Physics), Russia (Petersburg Nuclear Physics Institute), Switzerland (Paul Scherrer Institute) and the US (Los Alamos National Laboratory, North Carolina State University). We hope these new sources will make it possible to improve our measurements of the properties described in this article – as well as others not discussed, such as the neutron’s degree of neutrality and the spatial asymmetries in the way it decays (D Dubbers and M G Schmidt 2011 Rev. Mod. Phys. 83 1111).

As storage densities increase and losses are reduced, new applications of ultracold neutrons may become feasible. For example, the wavelength of ultracold neutrons is comparable to the diameter of a nanoparticle, and since they tend to bounce along a surface many times before being absorbed, it might be possible to use them as probes to study surface and interface physics at scales of a few angstroms. Long hailed as a means of probing fundamental theories about the nature of matter and the early universe, it is possible that these extremely cold particles could find a use in more down-to-earth applications, too.