Financial bonds are usually seen as safe and dependable investments, but a recent crash in the value of “ultra-long” bonds was bigger than conventional mathematical models could have predicted. They should have used rollercoaster physics, as Jon Cartwright explains

In the high-octane world of high finance, bonds are not usually the most exciting assets. Safe, slow, dependable, they are supposed to be the sensible choice for investors seeking long-term financial security. Often issued by governments that want to raise money to fund major projects, the bonds will be bought by investors who are effectively loaning their cash with guaranteed, long-term paybacks.
In 2022, however, the safety of bonds appeared to change. According to the US financial-analysis firm Bloomberg, the global bond market suffered an “unprecedented” loss between January and September of over 20%, in response to rising interest rates. Worse still, the value of a particular class of bonds – those that would mature and be cashed in over periods as long as 100 years – tumbled by as much as 60%.
To use a transport analogy, bonds have been behaving less like a smooth, dependable family saloon car, and more like a rollercoaster. In fact, the size of the losses has been beyond the usual predictors of bond behaviour. But for the physicist-turned-financier Jessica James, who is managing director at Commerzbank AG in London, the turbulence in the bond market came as no surprise.
In May 2021 James and two Commerzbank colleagues published a paper in the journal Quantitative Finance (21 1067), in which they pointed out that such a dramatic drop in value was a likely scenario – precisely because, as it turns out, very-long-term bonds and rollercoasters share similar physics. “There can,” says James, “be an extreme sensitivity to interest rate changes.”
Bonds: a simple guide
The basic concept of a bond is simple. It’s a debt, or an IOU: a contract between an “issuer” (such as a government or company) that needs to borrow money, and a “purchaser” (an insurance company, pension fund, bank or individual investor) that is prepared to loan the money for a specified time.
When that time is up, the bond is said to have reached “maturity” and the issuer must repay its debt in full. Until then, the purchaser can expect a regular stream of smaller payments, or “coupons”, from the issuer, which are a fixed percentage of the final sum. Issuers are usually large companies, banks or governments seeking to raise millions or billions of dollars.
Let’s say you buy a bond worth $1000 from an issuer with a coupon rate of 5% and a maturity of 10 years. As the purchaser, you’ve spent $1000, but will receive 5% × $1000 = $50 every year for the next 10 years, totalling $500. When the 10 years are up, the issuer will – hopefully – pay you back your original $1000.
That “hopefully” is important. Like any other financial investment, bonds carry a risk. The issuer might go bankrupt and be unable or unwilling to pay you back. And even if the issuer does pay you back in full, the money will – owing to inflation – not be worth as much as it once was in terms of purchasing power.
In our example, you can expect to accumulate a total of $500 in coupon payments once your $1000 bond has matured after 10 years. But if inflation is, like the coupon rate, 5%, then the $1000 itself will effectively have fallen in value by $629 compared with an equal investment that had kept pace with inflation. (The compounding effect of inflation means that 5% year-on-year equates to about 6.29% over 10 years.)
In other words, you’ll have lost more than you gained, and you’d have been better off putting your cash in gold or other investments that typically gain during periods of inflation. It’s why bond purchasers hope their coupon rates are much higher than inflation, so that their bonds retain their value, and on maturity realize net gains. And since interest rates tend to follow inflation, bond purchasers keep a close eye on inflation rates too.
Of course, if the economic situation looks bleak, a purchaser can always sell his or her bonds to someone else – for a price that reflects that new situation, and the current financial health of the issuer. In fact, that’s precisely what happened in the bond markets during 2022.

Time traders
As inflation and interest rates rose, maturity payments became less attractive in present value terms. Investors therefore saw their bonds plummet in value and so progressively sold them on the expectation that inflation will continue to rise and their bond values will continue to fall.
Existing bonds, therefore, have become less valuable assets. A bond that was worth, say, $1000 in January 2022, might have been worth only, say, $800 by September. This volatility in the value of a bond is reflected in the “yield”, which is roughly the coupon payment divided by the bond value.
In January the yield would have been $50/$1000 = 5%. But by September, the yield will have risen to $50/$800 = 6.25%. So if the bond falls, the yield gets bigger and the investment becomes poorer. The bottom line is that for anyone buying a bond, rising yields are bad news.
Enter the ultra-long bonds
Despite this uncertainty, bonds have traditionally been viewed as fairly safe investments relative to stocks, which on the whole promise greater returns, but at greater risk. In fact, almost anyone with a pension will own a few bonds via their pension provider, having bought them as part of a diverse portfolio.
Once a bond is paid off it ceases to exist, which means the bond market is the sum of all current bonds. Indeed, the global bond market is enormous. The International Capital Market Association has estimated that, as of August 2020, the overall size of global bond markets was worth $128.3 trillion ($128.3 × 1012).
Bonds have become so important largely because of the economic situation that nations in Western Europe, North America and elsewhere have faced since the 2008 global financial crisis. After a crash, people tend to tighten their wallets, businesses struggle and staff get laid off. In response, central banks try to stimulate the economy by cutting interest rates, which encourages people to borrow and spend more money.

But within months of the 2008 crash, interest rates were already very low, at just 1%. By 2020, they were even less, hovering close to zero. So like other central banks, the Bank of England created vast amounts of new money and used it to buy bonds issued by the UK government and large corporations. The method, known as quantitative easing, pushes up the overall price of bonds, which in turn drives down interest on bank loans, so people can borrow and spend more easily.
Within a year of the crash, the UK had bought £200bn of bonds for this purpose. By 2020, having also had a Eurozone debt crisis, Brexit and a coronavirus pandemic to contend with, that figure had risen to nearly £900bn.
Yet the sheer size might not be the most incredible aspect of the modern bond market. Historically, most bonds, government included, have had maturities between one and 30 years, reflecting the time periods over which people feel naturally inclined to speculate. But in recent years, a new type of bond has come to the fore, with “ultra-long” maturities of up to 100 years.
Several countries, such as Argentina, Austria and Mexico, have sold these century-long bonds. So too have large corporations, including the Walt Disney Company and Coca-Cola in the US. Even academic institutions, such as the University of Oxford in the UK, have sold them.
Although ultra-long maturities might seem ridiculous – most people will be long dead before the final pay out – they have proved attractive for investment groups or individuals who intend ultimately to sell their bonds and collect coupon payments in the meantime. In fact, James believes the rise of the ultra-long bond is directly due to the post-2008 economic situation.
“The problem is that when interest rates are very low, organizations like pension funds almost can’t invest,” she says. “They’re searching for any safe-looking instrument that has a positive yield associated with it. Also, bond issuers were keen to get folk interested in their debt. The one place you could still issue a bond with a positive coupon was in the very-long-maturity range.”
Jessica James: from physics to finance

Jessica James completed a PhD in theoretical atomic physics at the University of Oxford in 1994 under the supervision of Patrick Sandars, who had previously taught Stephen Hawking before the latter went to Cambridge. James admits she was “not going to be his next Hawking” – so when the First National Bank of Chicago approached the Oxford physics department for suitable postdocs, she was quick to accept a flight over for an interview.
Switching from physics to finance – to become a quantitative financier or “quant” – is these days a well-trodden path. But James claims that, when she got the job in Chicago in the mid-1990s, she was one of the first. With powerful computing becoming more widely available, the bank wanted to put more resources into modelling commodities mathematically, and to find out fair prices for bond contracts.
During her career in Chicago and at other banks, James has written books about her work, and in 2001 started an academic journal, Quantitative Finance. Originally part of IOP Publishing, which also publishes Physics World, the journal is now owned by Taylor & Francis. James has also written a Physics World Discovery ebook on the field.
Mathematical modelling
A physicist by training (see box above), James herself did not talk up the virtues of ultra-long-term bonds. Indeed, after moving into her current role at Commerzbank in 2012, she began to have doubts about the character of the ultra-long-term bond market. Despite not being complicated, the mathematics that’s used to estimate the sensitivity of the value of bonds to underlying changes in interest rates was, she feels, overly simplified.
To a first approximation, investors would assume that the relationship between total return and yield is linear, with a first derivative (i.e. slope) equal to the bond duration. In other words, the longer the duration, the more likely the return is to deviate from its original figure. If investors wanted to be more precise, they would plot the relationship between return and yield as a simple quadratic curve, with a second derivative known as “convexity” (due to the curve’s convex shape).
Convexity tends to look attractive for bond investors, says James, because it suggests that a bond holder will make bigger gains when interest rates and yields drop, and smaller losses when they rise. “The idea that convexity is good for bond holders has become totally embedded in the thinking process,” says James. “It made long-dated bonds look great.”
For James, however, there was an obvious reason to be cautious about very-long-term bonds. Over the course of a century, some degree of inflation is pretty much a given, making the final payback of a bond practically worthless. If, say, inflation were to average 5% year-on-year, as it has over the past 60 years, then a $1000 bond bought now would be worth, in real terms, about $7.60 in a century’s time.
It’s not that this isn’t understood. It’s bond maths and it’s relatively easy
Jessica James
“You don’t have the cushion of the final payment being a dominant part of the bond’s value, as you do in a short-term bond,” says James. “It’s not that this isn’t understood. It’s bond maths and it’s relatively easy. But usually it’s only these two derivatives [duration and convexity] that are looked at. The loss can be much higher.”
Looking past second derivatives is not unusual for physicists. When faced with a complex system or function, they are apt to approximate it to increasing degrees of precision by using a “Taylor expansion”. In other words, rather than just expressing the function using linear and quadratic terms, you also include cubics (third derivative), quartics (fourth derivative), and so on.
Engineers concerned with passenger vehicles are also familiar with higher derivatives. According to Newton’s second law, a force on a car, say, will give it an acceleration, which is the second derivative of position. But as any driver knows, suddenly applying a force (an accelerator or brake) is likely to cause passengers considerable discomfort, and possibly even a spilled coffee.
Vehicle designers therefore often try to minimize the third derivative of position, appropriately called “jerk”, which describes the rate of change of acceleration over time. Further comfort can be achieved by considering the fourth derivative of position, which is the rate of change of jerk, or “jounce”. It’s why modern rollercoaster loops are not circular, as you might expect, but teardrop-shaped.
Riding the big dipper
While they might both have their fair share of thrill-seekers, there is not much that theme parks and financial markets have in common. Still, James and her Commerzbank colleagues Michael Leister, Christoph Rieger and Hauke Siemssen wondered how much merit the inclusion of these higher, third and fourth derivatives of bond value with respect to yield had for risk assessment. As it turns out, quite a lot (figure 1).
When James and colleagues looked at models that included the higher terms, they realized that models incorporating duration and convexity alone had been underestimating gains when yields and interest rates fell, and underestimating losses when yields and interest rates rose. The effects were most apparent for very long bonds. “A 100-year bond is not a stable instrument,” says James. “It’s a highly volatile instrument.”
1 Century blues: the problem of ultra-long-term bonds
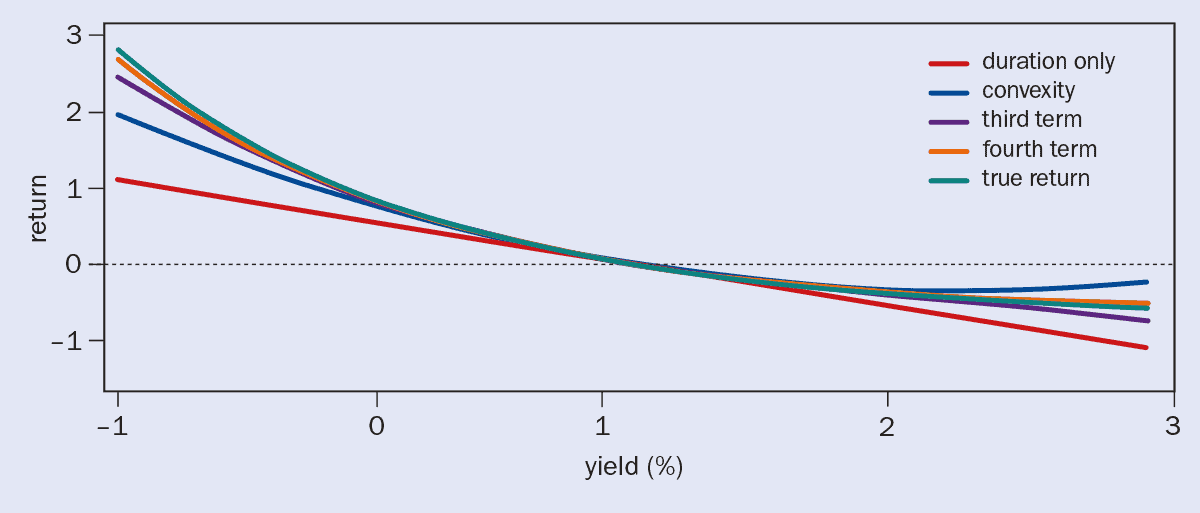
Jessica James, Michael Leister and Christoph Rieger from Commerzbank AG in Frankfurt and London have used mathematics to calculate the return for an ultra-long-term bond that matures in 100 years. This graph plots the return as a function of yield after a yield change, where yield is roughly the coupon payment divided by the bond value, with high yields being bad news for those buying the bonds (see main text). In this example, we’ve assumed the bond has a coupon payment of 2% with an initial yield of 1%. The return depends on how many terms are included in the mathematical series expansion of the return: first-order term only (“duration” – red curve); second-order term (“convexity” – blue curve), third-term (purple) and fourth-term (orange). Once you include higher terms, it is clear that models incorporating only first-order terms and second-order terms underestimate return at low yields – but underestimate the financial losses on these ultra-long bonds as yields rise.
In January 2022, some eight months after James and colleagues published their paper, their predictions were put to the test. In response to rapidly rising inflation, central banks across the world began to hike interest rates faster than at any time since the 1990s. The Bank of England, for example, raised the UK interest rate from 0.25% at the start of the year to 3% by November, with further rises due.
Suddenly, the real sensitivity of century bonds to interest rates became apparent. One issued by the University of Oxford, for example, dropped in value by nearly half, as did another issued by the German state of North Rhine–Westphalia. Yet another, issued by Austria – according to Bloomberg, one of the most highly rated government debtors – fell by over 60%.

Twists, turns, thrills and spills: the physics of rollercoasters
It is, of course, impossible to know how risky the purchasers considered these bonds. If they had estimated potential losses due to interest rate hikes on the basis of duration and convexity, as is common, they would have substantially underestimated the dangers. In the case of the North Rhine–Westphalia bond – which was issued in 2021 for €3bn – such an analysis would have predicted a loss of 35%. Had they considered third and fourth derivatives, however, they would have predicted a loss of 52% – within 2% of the actual figure.
David Blake, an economist at City, University of London, agrees that the inclusion of third and fourth derivatives improves the accuracy, and such calculations are “worth doing with very-long-term bonds”. He also says it is “quite neat” that James and colleagues have provided a straightforward means to include the derivatives in calculations of bond returns in response to yield changes via the derivation of “closed form” formulae, which can be computed in a finite number of steps. He adds, however, that the formulae will only work for standard, fixed-income bonds paying regular coupons, and not those depending on more complex contracts.
The power of new thinking
The collapse in the long-term bond market might deter investors from turning to such century bonds in the same way they once did. But, says James, they are unlikely to go away – not least because ultra-long-term debt has a longer history than many people can remember.
Gertrude Janeway, one of very few widows of American Civil War veterans who lived to see the 21st century, was still collecting a $70 pension cheque every month from the Veterans Administration when she died in 2003 – almost 140 years after the war ended. Meanwhile, in 2014 the UK government chose to redeem about £2.5bn of “perpetual” bonds (those without any fixed maturity) that it issued 300 years ago – before the Napoleonic Wars.
The message is clear. Very ultra-long-term debt is probably here to stay, and it will continue to thrill financiers – and physicists – with its ups and downs for many years to come.
• This article was corrected on 12 December 2022. A $1000 bond will have fallen after 10 years by $629, assuming inflation and a coupon rate of 5% (with the 5% year-on-year equating to about 6.29% over 10 years, not 6.5% as stated). Also a $1000 bond bought now would be worth, in real terms, about $7.60 in a century’s time (not $6.80 as originally stated).



