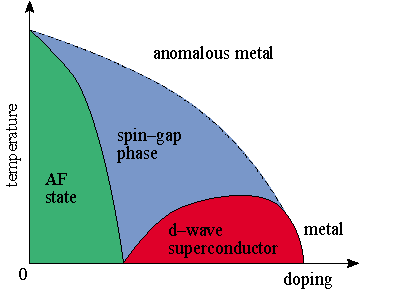
Even a decade and a half after the discovery of high-temperature superconductivity in ceramic compounds containing copper-oxide planes, these materials continue to puzzle condensed-matter theorists. The challenge is not simply to find a reasonable formula that predicts the uniquely high values for the superconducting transition temperature in the cuprates. Rather, superconductivity is but one aspect of the unique and complex phase diagram exhibited by this class of materials. Depending on the temperature and the level of doping, the cuprates can be insulators, metals or superconductors. The non-superconducting or “normal” phase also exhibits unusual properties (see figure).
Before the mid-1980s, superconductivity – which is defined as the absence of resistance to electrical current – had only been observed in metals and metallic alloys that had been cooled below 23 K. In 1986, however, Georg Bednorz and Alex Müller discovered that when lanthanum copper oxide, which is an insulator, is “doped” with barium, it becomes a superconductor with a transition temperature, Tc, of 36 K. Similar materials with higher transition temperatures soon followed, including yttrium barium copper oxide (YBCO), which has a Tc above the temperature of liquid nitrogen and opened up the possibility of new applications. The highest transition temperature currently known is 130 K in a mercury-based cuprate at room pressure. (Tc tends to increase with pressure.)
Amazingly, although more than 50 superconducting cuprates are now known, they are all variations on a single theme – lightly doped copper-oxide planes. Extensive research to find high-temperature superconductivity in other families of materials has been singularly unsuccessful. So what is so unique about the cuprates that enables them both to entice us with promises of novel applications and to challenge our fundamental understanding of electrons in solids?
A common feature of all superconductors – both the low- and the high-temperature variety – is that the electrons somehow overcome their mutual electrostatic repulsion to form “Cooper pairs”. Since these pairs do not have to obey the Pauli exclusion principle, they can condense into a single quantum state below a certain temperature. This is what gives superconductors their unusual properties. In low-temperature superconductors the electrons pair together so that their total orbital angular momentum is zero – a so-called s-wave state. Interactions between the electrons and phonons (vibrations of the crystal lattice) are responsible for the pairing.
In high-temperature superconductors, on the other hand, the pairs are in a so-called d-wave state, a superposition of states in which the angular momentum is non-zero. This d-wave symmetry has been clarified only recently by elegant experiments. But how does one turn the Coulomb repulsion between electrons into a form of attraction that binds the Cooper pairs together?
The phonon-based pairing mechanism in low-temperature superconductors requires the Coulomb repulsion to be described in terms of so-called Landau-Fermi liquid theory. In this theory the properties of single electrons are changed or “renormalized” by interactions with other electrons to form “quasiparticles”. The properties of the material can then be understood in terms of weak residual interactions between quasiparticles.
For many years, theorists worked with the Landau-Fermi theory – which has been remarkably successful in most metals – in an attempt to show that Cooper pairs with non-zero angular momentum could be formed from Coulomb repulsion alone. However, the cuprates never form a Landau-Fermi liquid. But what causes the breakdown of the Landau-Fermi liquid theory, which is otherwise so successful, and what is the nature of the resulting electron liquid?
Such a breakdown can occur near a symmetry-breaking transition, such as the transition from paramagnetism to antiferromagnetism (in which the magnetic moments or “spins” on neighbouring atoms point in opposite directions). This sort of transition leads to superconductivity in the so-called heavy fermion metals at high pressure. This direction is being followed by many groups, but others are sceptical. They point out that the Landau-Fermi model breaks down above the superconducting transition temperature and over a wide range of doping levels (see figure). They also point out that the onset of superconductivity is often the only symmetry-breaking transition that actually occurs. (Superconductivity breaks an abstract mathematical symmetry called gauge symmetry.)
If one rejects the above scenario, then one has to find a way to stabilize a non-Landau-Fermi liquid without a broken symmetry. Further, this new form of electron liquid should form a d-wave superconductor when cooled below a certain temperature. One promising approach is based on the idea of a doped resonant valence bond (RVB) state. The RVB state was first proposed by Philip Anderson many years ago to describe a lattice of antiferromagnetically coupled spins where the quantum fluctuations are so strong that long-range magnetic order is suppressed. The system resonates between states in which different pairs of spins form singlet states that have zero spin and hence no fixed direction in space. But how does a doped RVB state behave? And why does doping stabilize a RVB state when the undoped state prefers an ordered magnetic state? Currently a comprehensive theory is lacking, but there are encouraging signs.
The RVB state is just one of many theoretical approaches to high-temperature superconductivity. Other competing theories include those based on fluctuating stripes (in certain cuprates at low temperature the doped holes are observed to localize along parallel lines, called stripes, in the copper-oxide planes), and those that propose to unite the superconducting and antiferromagnetic phases in a larger symmetry group (so-called SO(5) theories). Other theories are based on the polaron mechanism and seek to exploit the strong coupling between electrons and phonons in oxide materials.
Lastly, we can ask what the final theory should predict. First, it should describe the full complex phase diagram. Second, it should reveal the special conditions in the cuprates that lead to this very special behaviour. From this should follow some suggestions for other materials that would show similar behaviour. While it may not be possible to predict Tc accurately – because, for instance, of a lack of precise input parameters – the final theory should give the correct order of magnitude and explain the trends that are observed in the cuprates. These trends include the increase in Tc as we move from single-layer cuprates to those containing two and three copper-oxide layers. These challenges are likely to keep theorists busy for years to come, but hopefully not another decade and a half.



