The recent discovery of magnetic materials that are also superconductors has reconciled two physical phenomena that were previously thought to be incompatible.

The startling transition of a metal into its superconducting state is revealed by the complete disappearance of electrical resistivity at low temperatures. Indeed, the current in a closed superconducting circuit can circulate forever without damping. Another fundamental property of the superconducting state was discovered in 1933 when Walther Meissner and Robert Ochsenfeld demonstrated that superconductors expel any residual magnetic field. Similarly, superconductivity can be destroyed by applying a magnetic field that exceeds some critical value.
Superconductivity and magnetism usually try to avoid each other – this feature can be exploited to, for example, levitate a magnet above superconductor. So the recent discovery of compounds that are both ferromagnetic and superconducting at the same time came as a surprise to many physicists.
Singlet and triplet superconductivity
The microscopic theory of superconductivity was created by John Bardeen, Leon Cooper and Robert Schrieffer in 1957. According to this so-called BCS theory, the electrons team up to form pairs, known as Cooper pairs, due to interactions with the crystal lattice at low temperatures. Electrons in these Cooper pairs have opposite values of momentum, meaning that the pairs themselves generally have zero orbital angular momentum. The formation of Cooper pairs also leads to the creation of a superconducting energy gap, which means that single electrons cannot occupy states near the Fermi surface. Such energy gaps – which are essentially equal to the energy needed to break up the Cooper pairs – show up clearly as exponential drops in the specific heat and thermal conductivity at what is known as the critical temperature, Tc.
The BCS theory is quite successful at explaining the properties of most superconductors. But the discovery in 1986 of a new class of materials that superconduct at high temperatures remains a challenge to theorists, and there is still no unambiguous theoretical explanation for this phenomenon.
The observation of superconductivity in organic conductors, heavy-fermion systems, the ruthenates and, most recently, the new ferromagnetic superconductors provides strong arguments for the existence of more exotic types of superconductivity. Indeed, superconductivity in ferromagnets must result from a different type of electron-pairing mechanism. In these materials, electrons with spins pointing in the same direction team up with each other to form Cooper pairs with one unit of spin, resulting in so-called triplet superconductivity. In contrast, conventional superconductivity – also known as s-wave singlet superconductivity – occurs when electrons with opposite spins bind together to form Cooper pairs with zero momentum and spin.
A magnetic field can destroy singlet superconductivity in two ways. The first of these effects is known as the orbital effect and is simply a manifestation of the Lorentz force. Since the electrons in the Cooper pair have opposite momenta, the Lorentz force acts in opposing directions and the pair breaks up. The second phenomenon, known as the paramagnetic effect, occurs when a strong magnetic field attempts to align the spins of both the electrons along the field direction.
Singlet superconductivity is destroyed by fields greater than Hp ~ 1.8Tc, where Tc is the critical temperature at which the material loses its electrical resistance. Such fields, however, do not wreck triplet superconductivity because the spins of both electrons may point in the same direction as the field. This means that triplet superconductivity can only be destroyed by the orbital effect.
Various types of magnetic ordering and superconductivity
Ferromagnetism arises when a large number of atoms or electrons align their spins in the same direction. There are actually two sources of magnetism in metals – localized magnetic moments and the “sea” of conduction electrons. Local magnetism occurs in rare-earth metals (such as gadolinium) and the actinides (such as neptunium) due to the incomplete filling of electrons in the inner atomic shells. This leads to a well defined magnetic moment at every fixed atomic site, which in turn produces long-range magnetic coupling due to the exchange of conduction electrons.
The second type of magnetism – known as band magnetism – arises from the magnetic moments of the conduction electrons themselves. In a metal, the electrons are “itinerant”, that is they are free to move from one atomic site to another, and they tend to align their magnetic moments in the direction of an applied field. This also occurs in the uranium-germanium alloys UGe2 and URhGe2, the two ferromagnetic superconductors that were recently discovered by groups at Cambridge University in the UK and at the French atomic energy commission (CEA) laboratory in Grenoble.
Ferromagnets only have a net magnetic moment at low temperatures; the internal magnetic field spontaneously appears at the so-called Curie temperature, which is typically in the range 10-1000 K. At higher temperatures, however, the magnetic moments of the atoms continually change their direction so that the net moment is zero. A similar magnetic transition occurs in antiferromagnets – materials in which the spins of neighbouring atoms point in opposite directions. This transition takes place at the Néel temperature and leads to the disappearance of the internal magnetic field.
Although superconductivity and magnetism seem to be antagonistic phenomena, could they co-exist in the same compound? This question was first posed by the Russian theorist Vitaly Ginzburg in 1957, but early experiments in 1959 by Bernd Matthias, then at Los Alamos, demonstrated that a very small concentration of magnetic rare-earth impurities – even a few per cent – was enough to completely destroy superconductivity when ferromagnetic ordering was present.
The origin of this destructive phenomenon is a quantum-mechanical interaction between the spins of the electrons and the atomic magnetic moments. Below the superconducting transition temperature, this “exchange interaction” attempts to align the Cooper pairs. Exchange interactions therefore place stringent limits on the existence of superconductivity.
However, superconducting crystals that have an antiferromagnetic sub-lattice of rare-earth atoms can, and do, exist. The first such materials – ternary compounds of rare-earth (RE) elements and molybdenum sulphide (REMo6S8) – were discovered in 1975 by Øystein Fischer’s group at the University of Geneva. Two years later Matthias, who was then at Bell Labs in New Jersey, and co-workers found the same behaviour in a series of rhodium-boride alloys (RERh4B4). Most of these compounds superconduct below a critical temperature between 2 K and 10 K, and undergo a magnetic phase transition in the range 0.5-4 K (see Fischer in further reading).
Neutron-scattering experiments have confirmed that the superconducting phase of practically all of these compounds has long-range antiferromagnetic order. Indeed, superconductivity and antiferromagnetism can co-exist quite peacefully because, on average, the magnetic moments in these compounds have almost no effect on the Cooper pairs – i.e. the exchange interaction is zero.
Internal conflicts
But can superconductivity and ferromagnetism co-exist? The answer to this question is much more fascinating. Some clues can be found in erbium rhodium boride (ErRh4B4) and holmium molybdenum sulphide (HoMo6S8) – the superconductivity of both these materials is destroyed by the onset of a first-order ferromagnetic phase transition.
For example, ErRh4B4 is a superconductor below 8.7 K. When it is cooled to the Curie temperature of 1 K, a “modulated” magnetic structure appears, rather than ferromagnetic ordering (figure 1). What this means is that neighbouring magnetic moments are aligned in the same direction, although the amplitude of the magnetization varies sinusoidally in space. But the ErRh4B4 remains superconducting at this temperature. Strictly speaking, the material is not ferromagnetic because it contains “domain-like” structures with alternating magnetic moments. This structure has been detected by neutron-scattering experiments and its period has been measured to be about 10 nm.
Moreover, in 1983 Sunil K Sinha, George Crabtree and co-workers at Argonne National Lab performed a simultaneous neutron-scattering and resistivity experiment on ErRh4B4. They showed that further cooling to 0.8 K brings about a first-order phase transition into the ferromagnetic phase and the superconductivity disappears. ErRh4B4 is a very rare example of a compound the superconducting properties of which are destroyed at very low temperatures.
What is the origin of such behaviour and what is the nature of the co-existent phase in the temperature interval between 0.8 K and 1 K? In the magnetic state, the presence of a localized atomic magnetic moment affects the spin distribution of the surrounding electrons due to the exchange interaction. This “induced” electron spin in turn interacts with the magnetic moments of other atoms – the so-called Ruderman-Kittel-Kasuya-Yosida interaction. The energy gained by the atoms due to the magnetic transition far exceeds the energy gained by the electrons as they form Cooper pairs at the superconducting transition. Thus magnetism is a much more robust phenomena compared with superconductivity. As a result, superconductivity cannot prevent the magnetic transition, it is only able to modify it.
The modulated ferromagnetic phase appears when ErRh4B4 and HoMo6S8 are cooled below their Curie temperatures. Phil Anderson and Harry Suhl pointed out in 1959 that the period of such sinusoidal magnetic structures, d, is greater than the atomic distance, a, yet smaller than the size of the Cooper pairs, xi (the so-called superconducting coherence length). Simply speaking, this magnetic structure looks like an antiferromagnet from the large-scale viewpoint of superconductivity because neighbouring domains point in opposite directions. But from the microscopic viewpoint of magnetism, the structure looks like a ferromagnet because the magnetic moments of neighbouring atoms point in the same direction (see Fischer in further reading).
However, the creation of domain walls costs energy, so at low temperatures it is energetically more favourable for all the magnetic moments to point in the same direction. Therefore ErRh4B4 turns into a true ferromagnet below 0.8 K and the superconductivity is destroyed.
Strictly speaking, there are no examples of materials in which singlet superconductivity and ferromagnetism co-exist. In all the known singlet ferromagnetic superconductors, like ErRh4B4 and HoMo6S8, a non-uniform magnetic phase appears in the superconducting state rather than a ferromagnetic phase. Similarly, it is very unlikely for singlet superconductivity to appear in the ferromagnetic state because the exchange interaction forbids the formation of Cooper pairs. Superconductivity and ferromagnetism looked destined to remain apart.
Superconductivity turns exotic
Until now we have only considered superconductivity caused by electrons located on the same atomic site teaming up to form Cooper pairs with zero spin. However, other pairings can occur – notably when there is a strong local Coulomb repulsion. This repulsion also plays a crucial role in the appearance of magnetism, helping to establish long-range order or slowly fluctuating magnetic correlations.
Unconventional electron pairing and magnetism are therefore often coupled, and understanding the interplay between the two phenomena is currently one of the key questions in condensed-matter physics. Magnetic interactions can also play an important role in attracting electrons to each other. Antiferromagnetic correlations lead to singlet pairing (with zero spin), while ferromagnetic correlations favour triplet pairing (with one unit of spin).
Another physical system where triplet pairing occurs is superfluid helium-3, and the long tradition of comparing superfluidity and superconductivity looks set to continue. Studies of helium-3 suggest that unconventional superconductivity will be highly anisotropic, i.e. it will depend strongly on the energy and momentum of the electrons. This means that any scattering by impurities in the material is likely to break apart the Cooper pairs. (In comparison, s-wave singlet superconductivity is much more robust and can only be destroyed by magnetic impurities that flip the spins of the charge carriers.) As a result, unconventional superconductivity can only appear in materials with a very high purity.
Superconductivity and itinerant magnetism at the critical pressure
Iron, cobalt and nickel are the best known metallic magnets, and their magnetic properties are governed by the conduction electrons that are free to move throughout the metal. These delocalized electrons populate an energy band that is filled up to the Fermi level, and they give rise to itinerant magnetism. The same band description governs the magnetic behaviour of the newly discovered ferromagnetic superconductors zirconium zinc (ZrZn2) and the uranium compounds UGe2 and URhGe2. In all of these materials, the electrons at the Fermi level are surrounded by a cloud of other charge carriers, which gives them a huge effective mass (up to 100 times greater than the mass of a “bare” electron) and causes them to move slowly. But if the density of states at the Fermi level becomes too high, then a magnetic instability will occur that splits the energy band into two, one part for “spin-up” electrons and one for “spin-down”.
Over the past few decades the theory of itinerant magnetism has been developed and a consistent approach has emerged called “spin-fluctuation” theory (see Springford in further reading). This approach describes how electrons are influenced by the fields produced by others in the Fermi sea. Moreover, spin-fluctuation theory is well suited to describing the “quantum critical point” where a small change in pressure destroys the magnetic ordering of atoms in a solid metal and the Curie temperature vanishes. These transitions are driven solely by quantum fluctuations, rather than thermal effects, and are characterized by a critical pressure, Pc (see Sachdev in further reading).
Quantum critical points have attracted a great deal of attention lately because the large slow spin fluctuations that occur near the critical pressure play a key role in the making and breaking of Cooper pairs. Moreover, experimentalists can apply a range of pressures to a material using a diamond anvil cell and look for any drastic changes to the properties around Pc.
Heavy-fermion systems, including the cerium-indium alloy CeIn3, are very sensitive to pressures – a tiny variation in density drastically modifies the low-temperature properties (figure 2). Many groups have studied the antiferromagnetic quantum critical point in heavy-fermion systems in detail, following pioneering work by Didier Jaccard at the University of Geneva in Switzerland on cerium copper germanium (CeCu2Ge2) a decade ago. More recently Gil Lonzarich’s group at Cambridge has discovered antiferromagnetic quantum critical points in cerium indium (CeIn3) and cerium palladium silicon (CePd2Si2). In all of these examples, the existence of superconductivity surrounding the quantum critical point strongly supports the spin-fluctuation theory.
Last year Siddharth Saxena and co-workers at Cambridge teamed up with Andrew Huxley and colleagues at Grenoble with the aim of studying a ferromagnetic quantum critical point in a polycrystalline sample of uranium germanium (UGe2). One of the current authors (JF) was quite reluctant to investigate UGe2 again as it had already been extensively studied by our Japanese colleagues. The same author was therefore surprised to discover that UGe2 became superconducting in the ferromagnetic phase (see figure 3 and Saxena et al. in further reading).
The findings partly confirmed a prediction of the spin-fluctuation approach that had been developed 20 years ago. According to this theory, a triplet superconducting domain should exist on both sides of the critical pressure. However, the experiments showed that it only appeared on the ferromagnetic side.
Dai Aoki and Huxley at Grenoble later found that uranium germanium had similar properties, while Christian Pfleiderer’s group at the University of Karslruhe in Germany revealed the same behaviour in the zirconium-zinc alloy ZrZn2. And earlier this year Katsuya Shimizu of Osaka University in Japan and co-workers reported superconductivity in the high-pressure phase of iron (see further reading). This latest breakthrough represents a milestone in superconductivity research, where one of the main goals is to discover the phenomena in simple elements. However, as we will explain later, the high-pressure hexagonal-close-packed phase of iron is not a ferromagnetic superconductor.
Uranium ferromagnets go superconducting
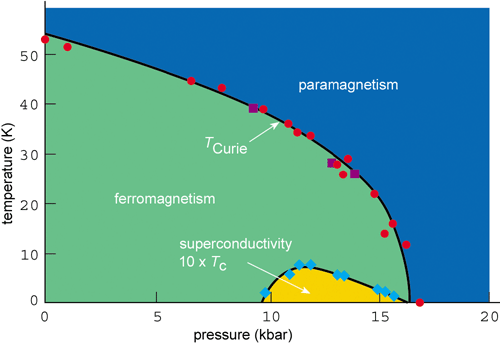
Physicists had believed that UGe2 was a good example of a so-called Ising ferromagnet. At ambient pressure, all the magnetic moments are aligned below 53 K. However, as increasing pressure is applied to the ferromagnet, the Curie temperature decreases rapidly and eventually vanishes at 17 kbars due to the presence of a quantum critical point (figure 3). Above the critical pressure, UGe2 is paramagnetic and the magnetic moments only align in the presence of a magnetic field.
The discovery of superconductivity in polycrystalline UGe2 by Saxena, Huxley and co-workers was just part of the story. They also found that the superconducting and ferromagnetic phases co-exist up to Curie temperatures of 30 K. Since the charge carriers experience a large effective magnetic field due to the alignment of spins, triplet pairing is a sound hypothesis.
At the same time, single-crystal studies at Grenoble demonstrated that UGe2 also displays the Meissner effect, one of the hallmarks of a superconductor. Soon afterwards microscopic neutron-diffraction experiments also proved the co-existence of superconductivity and ferromagnetism in UGe2. There was even the suggestion that superconductivity might be a bulk property of uranium ferromagnets.
The real proof of bulk superconductivity was obtained last year by Naoyuki Tateiwa and co-workers in Osaka. They observed a specific-heat anomaly at the critical temperature, a classic sign of a superconducting energy gap. The anomaly indicates that at least 15% of the sample superconducts and suggests that the underlying mechanism is due solely to the pairing of electrons with spins pointing “up”.
Recently, the Grenoble group discovered that uranium rhodium germanium (URhGe) is a ferromagnetic superconductor at ambient pressure. It has many similar properties to high-pressure UGe2 – it loses its resistance below 0.3 K, exhibits the Meissner effect and has a large specific-heat anomaly at the superconducting critical temperature.
Unlike UGe2, however, no high-quality crystals of URhGe have been produced so far. When this difficulty has been overcome, the observation of a ferromagnetic superconductor at ambient pressure will open the door to the same diverse range of experiments that have been carried out on the heavy-fermion superconductors, the ruthenates and the high-temperature superconductors. Moreover, new effects are expected to appear when the ferromagnetic domain structure is modified by magnetic fields or by changing the shape of the specimen. By altering the microstructure, we can create weak links between the ferromagnetic domains that should lead to new and interesting electronic networks.
ZrZn2: a promising case
Materials that exhibit itinerant magnetism without local magnetism have attracted a great deal of interest lately because the formation of the electronic band structure is simple. Earlier this year Christian Pfleiderer and co-workers at Karlsruhe made low-temperature measurements on samples of the weak ferromagnet ZrZn2 that had been prepared 10 years earlier by Stephen Hayden, who was then at Cambridge. The results showed that ZrZn2 superconducts only when it is a ferromagnet (i.e. below the critical pressure) and not when it is a paramagnet (i.e. above Pc).
ZrZn2 is a much weaker isotropic ferromagnet than UGe2 and URhGe. This means that coherent spin waves will appear below the temperature at which magnetic ordering sets in, while a transverse incoherent component will exist above. In comparison, only longitudinal modes are involved in UGe2. The big surprise was that superconductivity seems to exist up to 22 kbar and is weakly dependent on pressure, at least at low pressures. Once again there is no trace of superconductivity in the paramagnetic phase.
Curiously, the electrical resistance of ZrZn2 below the superconducting transition remains finite, rather than vanishing altogether (figure 4). In addition, there are no signs of any specific-heat anomaly at Tc. Both of these characteristics strongly indicate that superconductivity in ZrZn2 is inhomogeneous and only exists in clusters throughout the material.
Some theorists have argued that the disappearance of the Curie temperature and the superconducting critical temperature at the quantum critical point are sound justification of the phenomena. This may turn out to be the case, but the origin of the residual resistivity, and thus incomplete superconductivity, must be clarified. Either way, ZrZn2 is a promising example of a ferromagnetic superconductor and its true nature will be revealed by new experiments on crystals with improved purity.
Iron under pressure
Pressure can induce changes in crystal structure, and iron is no exception. Indeed, the high abundance of the element and the very high pressures deep inside the Earth’s core mean that the structure of iron is of special interest to geophysicists. The change in the crystal structure drastically modifies the magnetic properties of iron (figure 5).
The interplay of three crystal structures – dubbed the alpha, epsilon and gamma phases – and their electronic and magnetic properties can be represented on a pressure-temperature phase diagram. (The alpha, epsilon and gamma phases correspond to the body-centred-cubic, hexagonal-close-packed and face-centred-cubic crystal structures, respectively.) Moreover, the phase transitions that occur are all first order, and the transition between the alpha and epsilon phases has previously been studied in detail with the Mössbauer effect.
At low pressures and low temperatures, iron is the well known ferromagnet with a body-centred-cubic structure. As the pressure increases towards the quantum critical point at 40 GPa, the crystal structure changes to hexagonal close packed and magnetic measurements have shown the iron to be paramagnetic, rather like some heavy-fermion compounds. This suggests that spin fluctuations can occur with a rather low characteristic energy. According to Saxena and Peter Littlewood of Cambridge, this epsilon phase of iron is likely to be dominated by antiferromagnetic interactions, unlike similar structures in cobalt.
Recent resistivity experiments by Shimizu and co-workers at Osaka clearly show that the epsilon phase of iron does superconduct over a large pressure range (figure 5). The Osaka group has shown that its resistance drops by 10% at the critical temperature and it has a Meissner effect that is comparable with a reference sample of superconducting indium at 3.2 K (see figure 4). Here the finite resistance below Tc can be understood because the iron fails to turn into a pure hexagonal-close-packed structure due to experimental difficulties, and because the measurements were made with two gold leads (see lower part of intro figure).
As Saxena and Littlewood emphasized in an article in Nature about Shimizu’s work, the interest in the electric and magnetic properties of hexagonal-close-packed iron lies in the key role it plays in the inner core of the Earth and in stabilizing the planet’s magnetic field. Shimizu’s results will have a big impact as experimental groups rush to characterize the magnetic fluctuations in the epsilon phase. The first step will be to conduct resistivity measurements on a pure sample of epsilon iron and combine these finding with the Mössbauer results. The origin of the superconductivity in high-pressure iron may be antiferromagnetic, rather than ferromagnetic, but no-one knows for sure and the origin of the pairing mechanism remains a mystery.
Experiments versus theory
The theoretical debate on itinerant ferromagnetic superconductors starts with the idea of ferromagnetic spin fluctuations and predicts a superconducting phase on either side of the quantum critical point. But recent experiments reveal that superconductivity only occurs on one side. Krastan Balgoev of Boston College and co-workers have proposed that singlet pairing is restricted to the ferromagnetic phase, but their argument is, unfortunately, confined to low-energy excitations. Meanwhile, Ted Kirkpatrick of the University of Maryland has argued that superconductivity in weak ferromagnets (like ZrZn2) arises due to the coupling of longitudinal fluctuations with transverse spin waves.
For highly anisotropic materials like UGe2, Kazumasa Miyake and Shinji Watanabe at Osaka suggest that the majority of “spin-up” electrons may fulfil other conditions that lead to charge or spin-density waves with their own pairing mechanisms. Finally, classic electron-phonon coupling might also be possible in these complex materials since only the electrons on some small part of the Fermi surface may be coupled to ferromagnetism.
Goals for the future
Superconductivity and magnetism were long thought to be incompatible. Now various examples have been found thanks to improvements in the quality of samples that can be produced. The goals are to search for new examples and to formulate a theory that can explain the underlying pairing mechanism. Whenever new experimental data appear, the theoretical response is fast and leads to a number of different predictions and theories. What is clear, however, is that both the theoretical and experimental communities have been stimulated by the richness of the physics offered by these new materials. The race is now on to find a clear example of triplet pairing in a ferromagnetic superconductor.