
An international team led by researchers at Rutgers University in the US has found a way to create “flat” electronic bands – that is, electron states in which there is no relationship between the electrons’ energy and velocity – in graphene simply by causing the material to buckle. This new strategy could be used to produce so-called “superlattice” systems that serve as platforms for exploring the collective behaviour of electrons in strongly interacting quantum systems. Such behaviour is known to be linked to high-temperature superconductivity, but a complete understanding is still lacking.
Flat bands are especially interesting for physicists because electrons become “dispersionless” in these bands – that is, their kinetic energy is suppressed. As the electrons slow down almost to a halt, their effective mass approaches infinity, leading to exotic topological phenomena as well as strongly correlated states of matter associated with high-temperature superconductivity, magnetism and other quantum properties of solids.
A fine-tuning challenge
Flat bands are, however, difficult to engineer, and researchers have only observed them in a handful of physical systems. An example is twisted bilayer graphene, which is created by placing two sheets of graphene on top of each other and slightly misaligning them. Under these conditions, the atoms in the graphene sheets form a quasi-periodic moiré pattern with a period that is determined by the relative twist between the sheets’ crystallographic axes, rather than the spacing between individual atoms.
The result is a “superlattice” in which the material’s unit cell (that is, the simple repetition of carbon atoms in its crystal structure) expands to a huge extent – as if the 2D crystal were being stretched 100 times in all directions. This stretching dramatically changes the material’s interactions and properties. Notably, it undergoes a transition from an insulator to a superconductor at a “magic” twist angle of 1.1° and a temperature of 1.7 K.
“Magic angle” graphene has been studied extensively since its discovery in 2018. However, because the “magic” effect disappears at slightly larger or smaller twists, very accurate fine-tuning of the material is required to achieve the desired electronic band structure.
Pseudo-magnetic fields
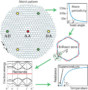
A team led by Eva Andrei of the Department of Physics and Astronomy at Rutgers has now developed an alternative means of producing flat electronic bands. She and her colleagues began by placing graphene on an atomically flat substrate of niobium diselenide or hexagonal boron nitride. Using scanning tunnelling microscope topography and computer simulations, they found that the graphene sheet buckled when cooled to 4 degrees above absolute zero. This buckling is driven by compressive strain within the graphene sample, which develops when ridges that formed during the sample’s fabrication collapse as it cools.
As the graphene buckles, a “mountain and valley” landscape forms that electrons in the material experience as pseudo-magnetic fields. “These fields are an electronic illusion, but they act as real magnetic fields,” Andrei explains. The result, she says, is a dramatic change in the material’s electronic properties – including the emergence of flat bands.
Researchers solve magic angle mystery
Unlike earlier realizations of a pseudo-magnetic fields that were mostly local in their extent, the buckling transition observed in this work produces a global change in the electronic structure of graphene, with a sequence of flat bands spread throughout the material.
According to the team, the new technique could thus become a general strategy for creating other superlattice systems and using them to explore interaction phenomena characteristic of flat bands.
The researchers, who report their work in Nature, say they would now like to develop ways of engineering buckled 2D materials with novel electronic and mechanical properties for use in applications such as nanorobotics and quantum computing.



