Particles called anyons that do not fit into the usual categories of fermions and bosons may lead to high-performance quantum computers, explains Frank Wilczek

Textbooks on quantum mechanics traditionally divide elementary particles into two types: fermions and bosons. Fermions such as electrons have antisymmetric wavefunctions, which means that a minus sign (i.e. a phase of π) is introduced into a system when two fermions in that system are interchanged. Bosons such as photons, on the other hand, have symmetric wavefunctions that do not change when two bosons are exchanged. Fermions and bosons also have different intrinsic angular momentum or spin: fermions have half-integer spins in quantum units, while bosons have integer spins.
But in 1977 a small band of theoretical physicists spearheaded by Jon Leinaas and Jan Myrheim at Oslo University in Norway realized that for particles living in two, rather than three, dimensions there are many other mathematical possibilities. Among these are particles that introduce any phase when they are interchanged, not just 0 or π.
In the early 1980s I named the hypothetical new particles “anyons”, the idea being that anything goes – but I did not lose much sleep anticipating their discovery. Very soon afterwards, however, Bert Halperin at Harvard University found the concept of anyons useful in understanding certain aspects of the fractional quantum Hall effect, which describes the modifications that take place in electronics at low temperatures in strong magnetic fields. In 1985 Dan Arovas, Bob Schrieffer and I, all of us then at the Kavli Institute for Theoretical Physics in Santa Barbara, proved that a successful theory of the fractional quantum Hall effect does indeed require particles that are neither bosons nor fermions. These developments spawned a vast literature, featuring beautiful and elaborate mathematics.
Until very recently, however, the subject of anyons had still been almost entirely theoretical. Suddenly, over the last few months, that has changed with the appearance of serious – though not entirely uncontroversial – claims that anyons have been observed directly. Meanwhile, several groups have proposed a new generation of experiments that will be more decisive in proving that anyons exist.
Fractional fluids
Strange things happen in semiconductors that are very pure, very cold and subject to strong magnetic fields. In particular, a phase of matter called a fractional quantum Hall effect fluid appears. In this state, electrons as we know them decompose so that electric charge is no longer transported in discreet lumps of charge e, but in fractions of that unit (see “Fractional quantum Hall effects”)
The fact that these fractional electrons are anyons could lead to a new kind of semiconductor technology that goes beyond electronics. An “anyonic” circuit would operate in ways that are impossible for conventional electronic circuits, and it is precisely this behaviour that physicists are ultimately hoping to exploit. Indeed, conceptual designs for anyonic quantum computers are already on the drawing board, such as those of Parsa Bonderson and co-workers at the California Institute of Technology (arXiv.org/abs/cond-mat/0508616).
To understand how these applications arise, we first need to introduce the idea of quantum statistics. In everyday life, we think of sameness as a limiting case of similarity: there are subtle distinctions between “identical” twins, for example. In quantum mechanics, however, objects can be truly identical. This profound identity is the basis of quantum statistics, and the reason behind the distinction between fermions and bosons.
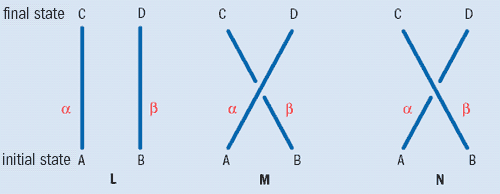
For instance, suppose that we want to calculate the probability that two identical particles α and β, which are originally at points A and B, will arrive at points C and D a certain time later. According to the rules of quantum mechanics, we can get this probability by adding the so-called amplitudes of every possible route that the particles can take to get from the initial to the final state, and then take the square of that sum.
If α and β are truly identical, then each of these possible routes leads to the same final state. For example, one route will leave α at position D and β at C, while another will leave β at C and α at D. Although the final state is the same, there is a clear distinction between the two ways of getting there: one is a direct process and the other is an exchange process (see Quantum statistics). We therefore need to supply a rule for how to properly combine the amplitudes of these topologically distinct processes. The simplest rule is to add them, and that rule defines bosons; the next simplest rule is to subtract them, and that defines fermions.
For many years, physicists thought that these two rules were the only consistent ones. In the case of particles moving in three (or more) dimensions, that is certainly the case. For particles confined to two dimensions, however, things are different. The reason is that there is no way to continuously deform the “over” process in which the path of particle α loops over particle β (path M in figure) – to the “under” process N without the paths of the two particles crossing one another. (Note that the rules of the game require these paths – which represent the world-line of the particle – to ascend through time without looping back, and that their end-points are fixed.)
Similarly, in 2D it is no longer true that doubling process M renders it trivial. Even though a and b will not have been interchanged, the doubled loop is even more entangled. This change opens up possibilities beyond the simple minus sign we had for fermions, and these possibilities essentially define anyons.
Anyons in reality
Talk of particles confined to two dimensions might seem more than a little academic, but 2D systems such as thin layers of semiconductors on insulating substrates are ubiquitous in microelectronics. The key insight is that quantum mechanics can suppress degrees of freedom. For instance, because atomic energy levels are discrete, the highest levels will not be accessible if a system is studied at sufficiently low energies and temperatures. As a result, certain kinds of motion cannot occur. If a semiconductor happens to be layered in such a way that the motion of electrons in the third dimension is quantized, then it can be rigorously considered as 2D.
Even to those of use who had been musing about the hypothetical possibility of anyons, their emergence as concrete physical realities in the theory of the quantum Hall effect in the mid-1980s came as something of a shock.
Although observable consequences of anyon behaviour are simple to sketch out, they are difficult to achieve experimentally. The latest experimental developments in the anyon story are all based on the same theme: a circuit consisting of a drop of fractional quantum Hall effect fluid with an island in the middle. An electric current can flow from one side of the drop to the other via two different paths, but if there are anyons on the island they will affect the way we add the contributions of these paths together. By studying the net current in the circuit, such a device is therefore sensitive to the presence of different numbers of anyons on the island. Last year Fernando Camino and co-workers at Stony Brook University were able to control the overall size of such an island using an applied voltage, which enabled them to create a “quasiparticle interferometer” (2005 Phys. Rev. B 72 075342). With it, the researchers detected the fringes that arise when particles with different fractional statistics interfere with one another, although the team did not attempt to introduce or resolve individual anyons.
That vital next step will be addressed by a new generation of experiments, such as those proposed by Sankar Das Sarma at the University of Maryland and colleagues (2005 Phys. Rev. Lett. 94 166802), Eun-Ah Kim and co-workers at the University of Illinois at Urbana-Champaign (2005 Phys. Rev. Lett. 95 176402) and Nick Bonesteel and co-workers at Florida State University (2005 Phys. Rev. Lett. 95 140503). The circuits in these experiments will contain several islands, allowing more intricate situations in which paths go over one island and under another. We can then imagine connecting islands together and moving anyons around, thus opening up the vast potential of anyonics.
Entering Hilbert space
Suppose that we are presented with a configuration of anyons and asked to predict how they will behave. In order to apply the rules of quantum mechanics, including the sorts of path-dependent factors described earlier, we have to know not only where the anyons are but also the likelihood that they arrived there in different ways. More precisely, what we need is the quantum-mechanical amplitude for each possibility. Achieving this would become a tricky proposition indeed if we had to keep track of their entire histories to find out how the particles’ world-lines got tangled up.
Alternatively, we can cast the problem in a different, more abstract space that includes a new variable – let’s call it “knottiness” – to describe the distinct classes of tangles. In this language, we need to know the amplitude for each value of knottiness. If we have a reasonably large number of particles, then their world-lines can get entangled in a very large number of different ways. Thus if we can access physical behaviour for systems of anyons that depends on their knottiness, we will have gained entry into a vast new space. We will, in fact, be wading into the oceans of quantum-mechanical Hilbert space.
Unfortunately, this knot-dependent information is difficult to maintain, measure and manipulate. Physicists are now just wetting their toes: learning to swim will be challenging indeed, and a quantum computer is a distant dream. Such a device would operate by moving anyons around, thus creating a highly structured knottiness that could be read-out by observing the behaviour of subsequent “probe” anyons. The vastness of Hilbert space offers enormous potential for increased storage space and bandwidth, and taming it is an inspiring goal for 21st-century physics. Anyonics might just provide the means to get us there.
More about: anyons
Parsa Bonderson et al. Detecting Non-Abelian Statistics in the μ=5/2 Fractional Quantum Hall State arxiv.org/abs/cond-mat/0508616
F. E. Camino et al. Realization of a Laughlin quasiparticle interferometer: Observation of fractional statistics Phys. Rev. B 72 075342
Sankar Das Sarma et al. Topologically Protected Qubits from a Possible Non-Abelian Fractional Quantum Hall State Phys. Rev. Lett. 94 166802
Eun-Ah Kim et al. Signatures of Fractional Statistics in Noise Experiments in Quantum Hall Fluids Phys. Rev. Lett. 95 176402
N. E. Bonesteel et al. Braid Topologies for Quantum Computation Phys. Rev. Lett. 95 140503