Martin Bucher reviews The Cosmic Web: Mysterious Architecture of the Universe by J Richard Gott
Does the large-scale universe look more like meatballs, like Swiss cheese or like a sponge? A meatball universe would be composed of isolated, disconnected regions of high density embedded in a connected low-density background. The Swiss cheese universe would be precisely the opposite: low-density isolated voids embedded in a high-density connected background. A sponge is neither of the above or, if you prefer, a compromise between the two. In a sponge both the low-density and high-density regions are each connected, and ideally both the sponge and its “complement” (the network of holes) are identical in character, at least from a topological point of view.
The differences between these various types of universe – and how we can use ideas from topology to quantify and statistically analyse them – are described in detail in J Richard Gott’s The Cosmic Web: Mysterious Architecture of the Universe. In essence, Gott’s book is the story of how our current understanding of the universe’s large-scale structure emerged over the past 100 years. Note that by “large-scale” Gott means scales somewhere between the entire observable universe (which comprises a sphere with an approximate radius of 15 billion parsecs, or about 45 billion light-years) and a distance of approximately 20 million parsecs. Below that scale the universe is at present very clumpy, and at least for the purposes of this book uninteresting.
Gott begins his story around 1918, when Harlow Shapley dethroned the Sun from its supposed position at the centre of the Milky Way by mapping the distribution of globular clusters. These compact, spherically shaped, gravitationally bound objects comprise thousands of stars and are predominantly situated in the halo of our galaxy, above its dust-obscured disc (part of which we see in the night sky as the Milky Way). Shapley observed that the density of globular clusters depends not only on the angle with respect to the disc; it is also higher in the direction of the galactic centre, which lies roughly in the constellation Sagittarius. Shapley’s analysis showed that if one regards the Milky Way as a sort of saucer, we live somewhere near the edge.
From there, Gott’s story follows two parallel but intertwined threads. The first concerns progress on the observational front. Over the past century or so, we have seen ever-bigger telescopes coming online, and in parallel instrumentalists have developed ever-better ways of capturing and processing images. Once CCD images replaced photographic plates analysed by eye, the linearity and reproducibility of CCD measurement made it possible to carry out accurate photometry – a prerequisite for constructing precision quantitative surveys.
Thanks to these advances, catalogues of galaxies increased both in size and in depth, in a manner much resembling Moore’s law, and the frontiers of the universe were progressively pushed back.
Indeed, one could describe these developments as a march outward in distance and backward in time, and ultimately to the limits of our “light cone”. Our past light cone consists of those events (characterized by a position and time) from which a signal can travel to us today along some path without the velocity ever exceeding the velocity of light. Today the terra incognita of the universe has all been mapped out, at least at some rudimentary resolution. We cannot look back farther, because doing so would require signals to travel acausally, or faster than the speed of light – which, as Einstein taught us, is not possible. There remain, however, some gaps to be filled in at higher resolution, such as the epoch of the formation of the first stars and quasars. Although some basic clues exist concerning this epoch, a precise mapping must await more powerful infrared telescopes, and in particular the Square Kilometre Array and its precursors.
The other thread of this story concerns the theoretical front. Improved maps duly inspired a wide range of theories that could explain the origin of the structures being mapped out. Since the quality of the data improved only slowly, a wide range of theories remained tenable for significant periods of time. Many of these theories had little in common, and decisions on which was correct (or at least still viable) had to await better data. In the meantime, the various possibilities gave rise to lively debates – debates that could not however be resolved until better data became available.
Gott’s book combines necessary background material presented in a clear and pedagogical manner with a personal narrative emphasizing those aspects of the subject to which he and his collaborators have made original contributions. Many of the anecdotes make fun reading, emphasizing the human aspect of the endeavour. Gott explains how as a high-school student, he was fascinated by the question of how to fill space using regular polyhedra. A project on this topic won him second place in the prestigious Westinghouse Science Talent Search, and this same idea was the subject of his first published paper, in the American Mathematical Monthly. More recently, this old interest inspired work on a quantitative measurement known as the “genus statistic”, which can be used to analyse the topology of large-scale structures (such as the meatball, Swiss cheese and sponge universes previously described) and thus decide between competing notions of structure formation.
To appreciate Gott’s work on the genus statistic, some background is required. We start with the fact that the large-scale structure of the universe is often explained as arising from an initial state in which matter was distributed uniformly with a certain average density r, with low-amplitude density irregularities dr(x) superimposed. In this model, the total density field is given by r(x) = r + dr(x). Mathematically, the simplest way to set up a stochastic model for the primordial cosmological perturbations is by means of a Gaussian stochastic process. The density perturbation field dr(x) is expanded into Fourier modes and the Fourier coefficient for each mode is chosen randomly and independently according to a Gaussian probability distribution whose variance depends only on the wavelength of the mode. This variance as a function of wavelength is known as the power spectrum of the Gaussian stochastic process and suffices to characterize this process completely.
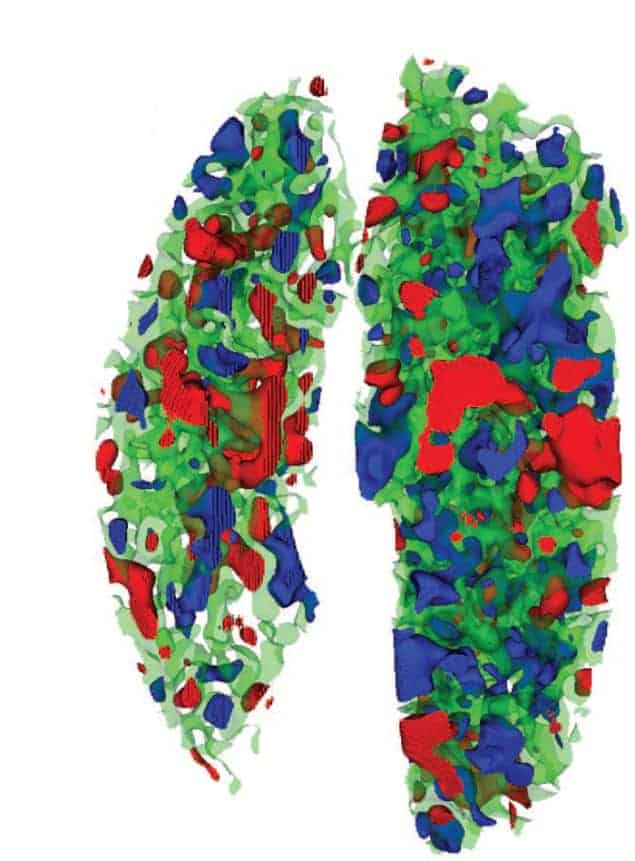
Because of the importance of Gaussian stochastic processes, most studies of large-scale structure focus on measuring the primordial power spectrum. This would be the end of the story if the primordial perturbations were indeed Gaussian. But Gaussianity should be tested by observation rather than decreed by fiat, and doing so requires new statistics beyond the power spectrum, because meatball-like or Swiss-cheese-like stochastic processes can be constructed with identical power spectra but appearances that are radically different to the eye. This is where the genus statistic comes in. It starts with a 3D catalogue of galaxies. The positions of these galaxies are used to create a smoothed galaxy density field rgalaxy(x,y,z), which is a sort of blurry approximation to the underlying density field r(x,y,z). Then the topology of the surfaces where rgalaxy(x,y,z) is constant is analysed; for example, the median density rmedian (defined as the density at which half the volume is more dense and the other half less dense) defines a 2D surface rgalaxyy(x,y,z)= rmedian. In a Gaussian theory this surface has the topology of a sponge, as shown in the figure above, which was produced using data from the Sloan Digital Sky Survey.
Today, the received wisdom is that the initial perturbations in the early universe were very nearly Gaussian random fields. The simplest inflationary models predict this, and recent extremely sensitive probes for primordial non-Gaussianity (particularly those using cosmic microwave background data) have failed to turn up any statistically significant evidence favouring a non-Gaussian stochastic process for the origin of the initial seeds of large-scale structure. But not so long ago the theoretical field was wide open, and models predicting different types of topology were able to explain the available data at the time. A Swiss-cheese universe, for example, might be explained as resulting from explosions, which would clear matter out of the voids.
This story, and the confusion it created within the cosmology community, is beautifully explained in Gott’s book. By going beyond a sort of “Cosmology 101” pseudo-history, in which observations are cherry-picked to suggest a linear path from past ignorance to current wisdom, Gott provides a complement to this more conventional story, artfully recounting the excitement, debates and false directions that led to our current “best bet” theoretical description of the universe.
- 2016 Princeton University Press £22.95/$29.95hb 272pp



