Ask a solid-state physicist to name the biggest discovery in the field over the past 50 years, and chances are the answer – if not high-temperature superconductivity – will be topological materials. These are materials in which bulk properties determine special behaviour along the surface or an edge, and they have profoundly changed the study of electrons in solids – as recognized by three Nobel prizes. Their earliest incarnations in physics have created a new standard for electrical resistance, and provided an independent means to determine the fine-structure constant, α, in quantum electrodynamics. These materials are also expected to bring great advances to information processing, resulting from topological electron behaviour in graphene, or the harnessing of topological qubits in quantum computing. Even exotic entities such as magnetic monopoles and Majorana particles, once a province of particle physics, have become the subject of solid-state topological study.

But now topology is going beyond the solid state. In the past few years, physicists have begun to realize that it could have a major role in fluid dynamics – the Earth’s oceans, for example, or plasmas, or the biological cells in fluid-like “active” matter. The research promises to provide a clear window through which to study what can otherwise be very murky areas of science. More importantly, it brings an entirely new area of mathematics to our understanding of the natural world; as well as to complex artificial systems of huge practical importance, namely fusion reactors. “Topology gives you a quick, direct way to see whether waves [in certain systems] exist,” says theorist Brad Marston of Brown University in Rhode Island. “Once you work through the logic, answers can come very simply.”

Topological research promises to provide a clear window through which to study what can otherwise be very murky areas of science

At the edge

Topology as a mathematical concept goes back a long time, at least to the 19th century. It describes properties of objects that do not change during continuous deformations. For example, a Möbius strip will always have one continuous edge and one continuous surface, no matter how much it is stretched or twisted. Similarly, a mug and a doughnut are topologically identical, if defined by the existence of a single hole. Topology is also what properly differentiates a line from a surface and, more broadly, what constitutes a dimension.

Physics, however, has not always been quick to see where topology matters. Indeed, the first topological property in the solid state was initially not even recognized as such. This is the quantum Hall effect, which concerns electron behaviour in a very thin (and therefore essentially 2D) semiconductor that is sandwiched between two other semiconductors. When a magnetic field is applied, the electrons in the 2D layer experience a perpendicular Lorentz force and begin to travel in tiny circles, similar to the orbits of bound electrons around atoms.

This is possible for all the electrons apart from those near the semiconductor’s edges, where there is not enough space for complete circles. Here, the electron trajectories are chopped off into semicircles – whenever each electron gets to the end of its semicircle, it zips straight along the edge itself. Thanks to the particular behaviour of these edge electrons, the edge itself becomes electrically conducting – unlike the interior of the semiconductor, which remains non-conductive.

The importance of the quantum Hall effect was immediately obvious after its discovery by the German physicist Klaus von Klitzing in 1980. As implied by the name, it stems from the conductance being perfectly quantized – a fact that has been exploited for the new international standard for electrical resistance (the ohm), and for precise determinations of α. Two years after von Klitzing’s discovery, the topological nature of the effect began to become apparent, thanks to work by the British theorist David Thouless. Both von Klitzing and Thouless won the Nobel Prize for Physics for their contributions, in 1985 and 2016, respectively.

Read more

David Thouless, Duncan Haldane and Michael Kosterlitz win 2016 Nobel Prize for Physics

Topological properties often involve behaviour in a certain dimension manifesting as something else – something much less trivial – in a lower dimension. As such, there is an intuitive sense in the quantum Hall effect being topological in origin: the straight, 1D trajectories the electrons take at the edges of the semiconductor can be viewed as projections of the 2D circles they take within. Topological properties sometimes also involve the breaking of one or more fundamental symmetries. In the case of the quantum Hall effect, the external magnetic field breaks time-reversal symmetry, such that solutions to the Schrödinger equation describing electron behaviour are no longer identical when time, t, is replaced by –t.

Robust effects

But it is not only the conductivity, and the quantization of that conductivity, that makes the quantum Hall effect special. Another topological hallmark is the robustness of the conductivity in the face of defects, temperature changes and other forms of disruption: the phenomenon is “topologically protected”. It is for this reason that the quantum Hall effect is earmarked for applications in computing, including quantum computing using qubits, which are notoriously hard to sustain against environmental decoherence.

Despite Thouless’s insight, it was not until the 2000s that interest in topology in the solid state really took off. This was after the prediction, and subsequent discovery, of edge conductance in thin insulators in the absence of an external magnetic field. Electrical insulators in the bulk, topological insulators have surface states that conduct electrons extremely well. In 2D topological insulators, an effective magnetic field is generated by every electron as its spin interacts with its orbital motion. The result is a quantum spin Hall effect, wherein spin-up and spin-down electrons travel in opposite directions along an edge. Shortly after the discovery of 2D topological insulators, physicists found examples of topological insulators operating in 3D: for these, it is electron behaviour in a 3D volume that manifests as spin conductance over a 2D surface.

Beyond the solid state

Today, topology is a huge topic in physics. But all this topological research has had one feature in common. It is physics of the solid state, or at least physics involving a discrete, periodic lattice (if topological photonics, another emerging topic, is to be included). That all changed in 2017 when Brown University’s Marston, together with Pierre Delplace and Antoine Venaille at the University of Lyon in France, studied the fluids that make up the Earth’s atmosphere and oceans from a topological perspective.

They were particularly interested in certain, unusual waves in the atmosphere and oceans at the equator, known as Kelvin and Yanai modes. Geophysicists had first identified these waves in the 1960s, describing them as classical solutions to the wave equation, but there were still numerous unknowns about them. They are confined to the Earth’s equator; they are persistent; and they only travel eastwards, never westwards. A condensed-matter physicist by training, Marston had already spent a decade statistically simulating fluid aspects of the climate system at mid latitudes before he came across these strange equatorial waves. “I could have made this connection 10 years earlier if I had been paying closer attention,” he says now. “This is what happens when scientific fields fragment. Geophysicists don’t go to condensed-matter seminars, and vice-versa. They aren’t exposed to topological ideas.”

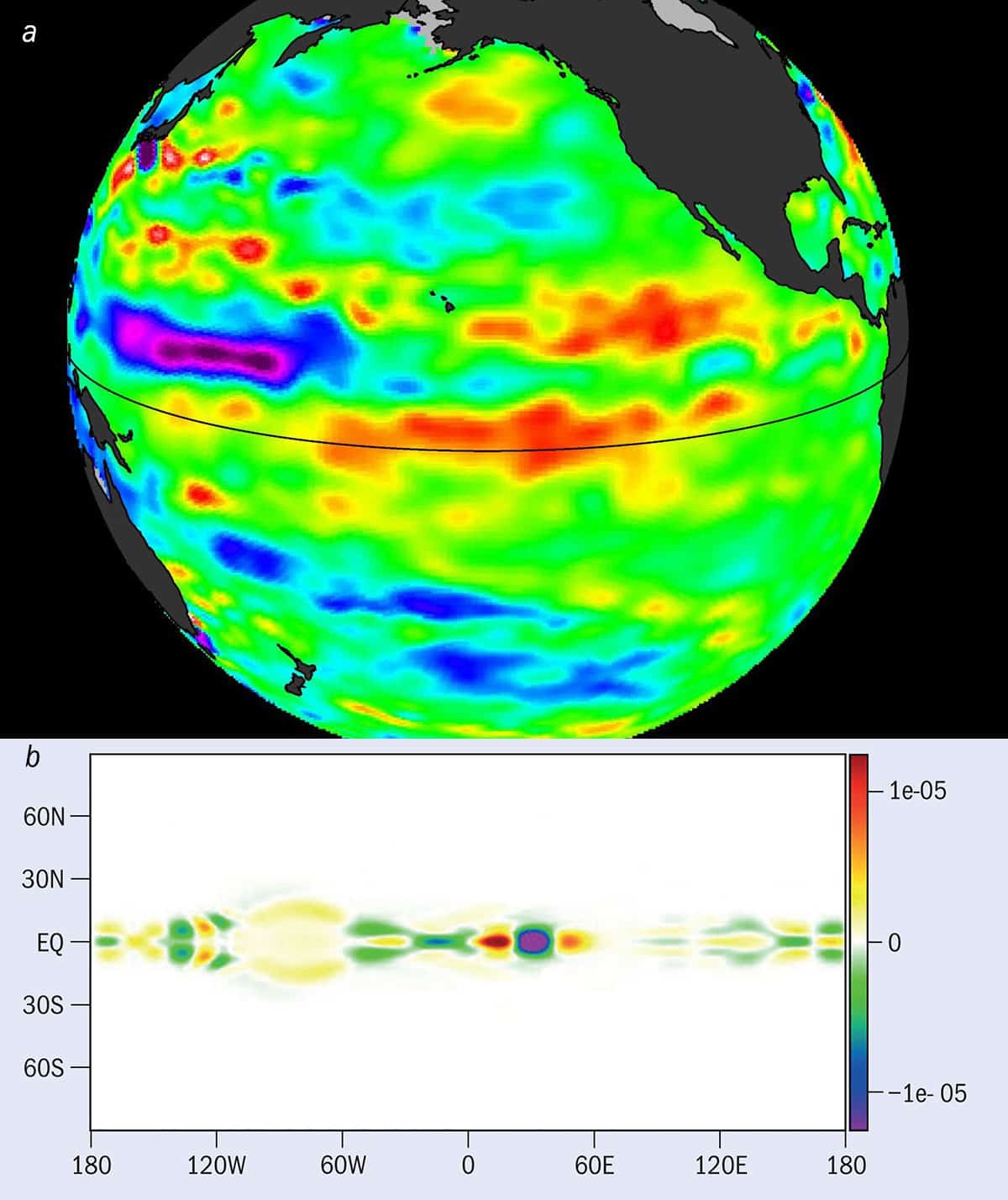
Helped by Marston’s background, the three researchers immediately noticed that these equatorial waves had topological characteristics. First of all, the slim layers of the Earth’s atmosphere and oceans can be approximated as 2D. Second, the constituent air and water molecules are, like electrons in the quantum Hall effect, encouraged into circular motion by a force acting perpendicularly to that motion – in this case the Coriolis force (which results from the Earth’s rotation). Like the magnetic field in the solid-state phenomenon, the Coriolis force breaks time-reversal symmetry. It also forms a natural boundary, or edge, at the equator, deflecting air and water currents clockwise in the southern hemisphere, and counter-clockwise in the northern hemisphere. With such ingredients, says Marston, it is possible to ascertain fairly quickly via topology that persistent waves should exist at the equator, regardless of the finer details of the Earth’s climate and ocean systems (figure 1).

But how many waves? All topological properties have a characteristic integer value, the first Chern number (named after the Sino-American mathematician who identified it in the 1940s), which is one way to find how many unique states the property should give rise to. In their study, Marston and his colleagues calculated a first Chern number equal to ±2, corresponding to two edge modes. Using topology, and without having to solve any classical wave equations with ungainly polynomials, the researchers had proved that the equator should harbour two unidirectional equatorial waves – the Kelvin and Yanai modes (Science 358 1075). Both of these waves are known to influence the El Niño Southern Oscillation in the Earth’s ocean–atmosphere system, which in turn has a significant climate impact, causing incidents of drought or flooding in equatorial countries. According to Marston, topological insights could help researchers model El Niño and other oscillations, which have hitherto been sources of high uncertainty in climate predictions.

Active flow

Inspired by a talk Marston gave on the results, a group led by Cristina Marchetti at Syracuse University, New York, swiftly explored topology in a very different type of fluid system: active matter. Such matter consists of any collection of units that are able to propel themselves by some means. There are numerous examples in the natural world, from flocks of birds to bacterial suspensions and migrating cells. Active matter often flows in thin layers, for instance through skin or the lining of the gut. And, like the Earth’s atmosphere, these layers often have a curvature – in the case of the eye, even an Earth-like spherical geometry. The difference with the Earth’s atmosphere is that biological active matter is not subject in any significant way to a perpendicular external force such as the Coriolis force. But the fact that the matter is active and propels itself breaks time-reversal symmetry.

In their analytical computation, Marchetti and colleagues found that the combination of active flow and curved geometries supports topological waves around the equator of a sphere, or the neck of an hourglass-shaped object known as a catenoid (figure 2). In a very general sense, the researchers say, these topological waves provide highways for information transfer within a flock, which are robust against disorder and backscattering (Phys. Rev. X 7 031039).

Marchetti’s group was not considering any particular type of active matter, and Suraj Shankar, a former member who is now based at Harvard University, US, is at pains to say that biology is too complex to speculate about the importance of the effect for particular systems. However, he does point out that some types of active matter are already known to harbour waves. For instance, the cells involved in wound healing transmit stress waves, which scientists believe may be involved in guiding the tissue’s growth and maintaining its integrity until the wound is fully healed. Given that wounds often occur on curved parts of the body, says Shankar, “it is not inconceivable that you end up with situations where these waves have a topological character”. Although experiments with active matter are difficult, and those on curved surfaces doubly so, he adds that other groups are already trying to observe the tell-tale signs of topology in active-matter systems.

Fluid topology

More and more research is turning to topology in fluids. A group led by Anton Souslov at the University of Bath in the UK, for example, has shown that in an active-matter system comprising chiral units, it is possible to design an interface that topological waves can flow into but not out of – a phenomenon that could be exploited to build perfect absorbers for soundproofing (arXiv:2010.07342). Meanwhile, Delplace, Venaille and Manolis Perrot at the University of Lyon have used topology to predict new types of trapped acoustic-gravity waves, known as Lamb waves. Observations of such Lamb waves could give us insight into the otherwise-invisible details of the stratification of distant planetary atmospheres, they say (Nature Phys. 15 781).

But perhaps the most intriguing area of this new fluid topology, from an application point of view, is plasmas. For these insights, we can thank a chance meeting of Marston with an old friend, Jeff Parker, a theoretical plasma physicist at Lawrence Livermore National Laboratory in California. The duo crossed paths at a fluid-dynamics workshop at the Aspen Center for Physics, Colorado, in 2017. By his own admission, Parker at the time knew very little about topology and the quantum Hall effect, but on hearing about Marston’s early work on geophysical waves he immediately saw similarities to models used in plasma physics. “I thought if it applies to fluids, it applies to plasmas,” he says. “It was intriguing to me – I was excited to be one of the first to look into it in plasmas.”

I thought if it applies to fluids, it applies to plasmas. I was excited to be one of the first to look into it in plasmas

Jeff Parker

Plasma waves

Marston and Parker began to work together, along with Ziyan Zhu at Harvard University and Steven Tobias at the University of Leeds in the UK. In a first foray into the topology of plasma physics, the researchers considered a system in which a magnetic field confines a plasma to a long cylindrical geometry. They found that, according to the topology of the system, a surface wave of electrons – what they term a “gaseous plasmon polariton” – should manifest along the outer boundary, where the plasma abruptly peters out into a vacuum (Phys. Rev. Lett. 124 195001). They have arranged to test their prediction at the Basic Plasma Science Facility at the University of California Los Angeles once COVID-19 restrictions have eased.

Having tested the waters of plasma topology, the same researchers, without Zhu but including Joshua Burby at Los Alamos National Laboratory in New Mexico, considered a more exciting system: the tokamak. In any radial cross-section of this doughnut-shaped geometry, contour lines can be drawn to represent the magnetic shear (where the magnetic field changes direction) in the ions making up the plasma. Parker, Marston and colleagues found that a magnetic shear varying from negative to positive from one slice to the next indicates the presence of a boundary with a Chern number of +1 on one side and –1 on the other. The ions at this boundary will therefore harbour a topological wave (Phys. Rev. Research 2 033425) (figure 3).

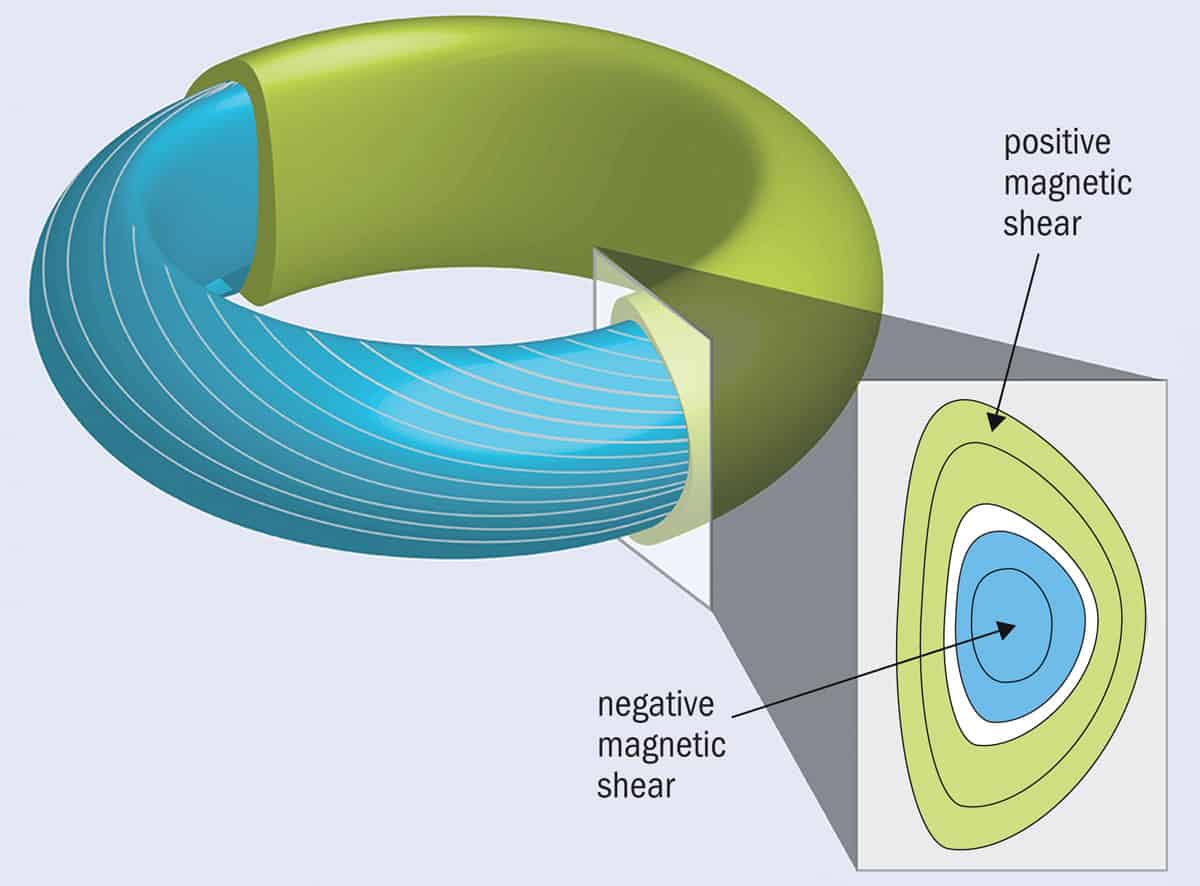
In fact, experimental plasma physicists are already aware of such waves. They are known as a reversed-shear Alfvén eigenmodes (RSAEs), and are something of a double-edged sword. On one hand, they can resonate with the products of a fusion reaction – alpha particles – causing them and their associated energy to be ejected from the confinement before they can be harnessed for fusion power. On the other hand, their characteristics can betray details about the magnetic-field structure of the plasma in the middle of a tokamak, where extreme conditions make it difficult to perform conventional diagnostics. Retrospectively predicting the existence of RSAEs, as Parker, Marston and colleagues have done, does not alter any of this physics. As in the case of equatorial waves in the Earth’s atmosphere and ocean systems, however, the result provides the tantalizing prospect of more topological insights into tokamaks, which can currently only confine plasmas from minutes to hours before they fizzle out.

Might it be possible that, with more study, physicists could find the tokamak conditions that deliver a topologically protected state of fusion – in other words, one that can be sustained indefinitely? “I think it’s a little way off, but that’s the dream,” says Parker. He believes the goal is analogous to exploiting the quantum Hall effect for stable qubits in quantum computing. That is, a goal that is speculative, but reasonable. Certainly, the physics of topological fluids is only just getting started. With applications already ranging from the Earth’s climate to active matter to plasmas, who knows what it will illuminate next?