As theories go, quantum mechanics has certainly been successful. Despite its many counterintuitive predictions, it has provided an accurate description of the atomic world for more than 80 years. It has also been an essential tool for designing today’s computer chips and hard-disk drives, as well as the lasers used in the fibre-optic communications of the Internet. Now, however, the ability to manipulate the quantum states of individual subatomic particles is allowing us to exploit the strange properties of quantum theory much more directly in information technology.

We are used to thinking of information as being abstract, but in fact all information requires a physical medium for its processing, storage and communication. The basic unit of information – a bit that is either “0” or “1” – can be represented physically by, for example, the current in a circuit or light in an optical fibre. As information is represented by ever smaller physical systems, quantum effects become increasingly important. The ultimate limit comes when bits are represented by the quantum state of a single particle, such as the polarization of a photon.

Applied to information, quantum theory throws up some very odd predictions. These are not only interesting as a test of quantum mechanics, but can also bring us practical applications that are simply impossible with “classical” information technology. For example, a quantum computer would work with bits that can be both “0” and “1” at the same time, allowing it to solve certain mathematical problems – such as factorizing very large numbers – that are virtually intractable using an ordinary computer.

Although practical quantum computers will take many years to develop, one manifestation of quantum information technology is already a reality: quantum cryptography. This ultra-secure way of sending messages is based on the fundamental postulate that measuring a quantum state will, in general, alter it. Thus, if we encode messages in individual quantum states, such as the phase of photons whizzing down an optical fibre, an eavesdropper who tries to intercept the message cannot avoid changing it. We can therefore test if the message has been read before it reaches the intended recipient – something that is impossible using classical signals.

The commercial potential of quantum cryptography has attracted private investment in several start-up companies in the US and Europe. The firm id Quantique, for example, spun out from pioneering research at the University of Geneva; while in the US, commercial developments are led by MagiQ Technologies, based in New York and Massachusetts. Recently a third start-up called SmartQuantum has been established in Brittany, France, and major corporate players such as HP, IBM, Mitsubishi, NEC, NTT and Toshiba all have active quantum-cryptography programmes. With several quantum-cryptography products already on the market, the quantum information industry has arrived.

The key to security

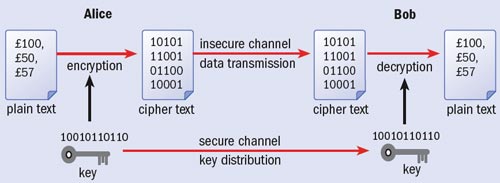
Cryptography is a vital part of today’s computer and communication networks, protecting everything from business e-mails to bank transactions and Internet shopping. Information is generally kept secret using a mathematical formula called an encryption algorithm, together with a secret “key” that the sender uses to scramble a message into a form that cannot be understood by an eavesdropper. The recipient then uses the same key – typically a long binary number – with a decryption algorithm to read the message.

Although modern algorithms such as the Advanced Encryption Standard (AES) are very hard to break without the key, this system suffers from an obvious weakness: the key must be known to both parties. Thus the problem of confidential communication reduces to that of how to distribute these keys securely – the encrypted message itself can then safely be sent along a public channel (figure 1). A common method is to use a trusted courier to transport the key from sender to receiver.

However, any distribution method that relies on humans is vulnerable to the key being revealed voluntarily or under coercion. In contrast, quantum cryptography, or more accurately quantum key distribution (QKD), provides an automated method for distributing secret keys using standard communication fibres. The revolutionary feature of QKD is that it is inherently secure: assuming that the laws of quantum theory are correct, we can prove that the key cannot be obtained by an eavesdropper without the sender and recipient’s knowledge. Furthermore, QKD allows the key to be changed frequently, reducing the threat of key theft or “cryptanalysis”, whereby an eavesdropper analyses patterns in the encrypted messages in order to deduce the secret key.

The first method for distributing secret keys encoded in quantum states was proposed in 1984 by theoretical physicists Charles Bennett at IBM and Gilles Brassard at the University of Montreal. In their “BB84” protocol, a bit of information is represented by the polarization state of a single photon – “0” by horizontal and “1” by vertical, for example. The sender (Alice) transmits a string of polarized single photons to the receiver (Bob) and by carrying out a series of quantum measurements and public communications they are able to establish a shared key and to test whether an eavesdropper (Eve) has intercepted any bits of this key en route.

The BB84 protocol allows us not only to test for eavesdropping, but also to guarantee that Alice and Bob can establish a secret key even if Eve has determined some of the bits in their shared binary sequence, using a technique called “privacy amplification”. Imagine, for example, that Eve knows 10% of the key bits shared by Alice and Bob. Being aware of this, Alice and Bob could then publicly agree to add together (using modular arithmetic) each adjacent pair of bits to form a new sequence of half the length. Eve may also do this, but since she will need to know both bits in a pair in order to correctly determine their sum, she will find that she now shares a much lower fraction of the new bit sequence with Alice and Bob.

So much for the principle. In practice, generating the pulses of single photons required for BB84 is not easy. Despite recent progress using single atoms or semiconductor quantum dots to generate single photons (see Physics World February 2003 “Single photons on demand”), most practical QKD systems use weak laser pulses to send the bits that make up the key. This method has an Achilles heel: the laser will sometimes generate pulses containing two or more photons, each of which will be in the same quantum state. As a result, Eve could split off one of these photons and measure it, while leaving the other photons in the pulse undisturbed, thus determining part of the key while remaining undetected. Even worse, by blocking the single-photon pulses and allowing only the multi-photon pulses to travel through to Bob, Eve could determine the entire key.

Until true single-photon sources become available commercially, the most common defence is to strongly attenuate the laser to limit the rate of multi-photon pulses. However, this also means that many pulses contain no photons at all, reducing the rate at which the key can be transmitted. In 2003 a new trick to get round this problem was proposed by Hoi-Kwong Lo at the University of Toronto and Xiang-Bin Wang at the Quantum Computation and Information Project in Tokyo, based on earlier work by Won-Young Hwang at Northwestern University in the US.

Their idea was to intersperse the signal pulses randomly with some “decoy pulses” that are weaker on average and so very rarely contain a multi-photon pulse. If Eve attempts a pulse-splitting attack, she will therefore transmit a lower fraction of the decoy pulses to Bob than the signal pulses. Thus by monitoring the transmission of the decoy and signal pulses separately, Eve’s attack can be detected. This means that stronger laser pulses may be used securely – for instance, last year at Toshiba we demonstrated a 100-fold increase in the rate that keys can be transmitted securely over a 25 km fibre. The decoy-pulse protocol has caused great excitement in the QKD community, with four independent groups having just reported experimental demonstrations of the technique.

Weak laser pulses are not the only way to carry out quantum cryptography. For example, QKD using a true single-photon source has recently been demonstrated at Stanford University, the CNRS in Orsay and Toshiba. Furthermore, in 1991 Artur Ekert, while a PhD student at the University of Oxford, described an alternative to the BB84 protocol that exploits another counterintuitive prediction of quantum mechanics: entanglement. Pairs of entangled photons have quantum states that are strongly correlated, such that measuring one photon affects the measurement of the other. If Alice and Bob each have one of the pair, they can therefore use their measurements to exchange information. This technique has been demonstrated by researchers at the University of Vienna, the Los Alamos National Laboratory and the University of Geneva, and was even used in 2004 to transfer money between Vienna City Hall and an Austrian bank. However, weak-laser QKD is the most mature approach, and the basis of the commercial QKD systems that are now coming on the market.

Practical QKD

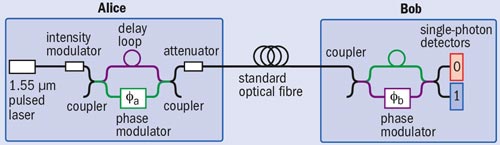
Information can be encoded in the quantum state of photons in several different ways. The first laboratory demonstration of QKD by Bennett and Brassard in 1989 over 30 cm of air used the polarization state of photons. However, transmitting photons along an optical fibre can randomize their polarization, so a better approach pioneered by Paul Townsend, formerly of BT Labs in the UK, is to alter the phase of the photon. In this method, weak laser pulses are injected into an interferometer by Alice. By applying different voltages to a “phase modulator” in one arm of the interferometer, Alice can encode bits as a phase difference between the two emergent pulses sent to Bob – for example with 0° representing “0” and 180° representing “1”. Bob then passes the pulses through another interferometer and determines which of his two detectors, corresponding to “0” and “1”, they emerge at (see figure 2).

For this scheme to work, we must keep the relative lengths of the interfering paths in Alice and Bob’s interferometers stable to a few tens of nanometres. However, temperature changes of just a fraction of a degree are enough to upset this balance. An ingenious solution to this problem was introduced by the Geneva group in 1997, which led to the first QKD system suitable for use outside the lab. The idea is to send the laser pulses on a round trip from Bob to Alice and then back to Bob so that any changes in the relative arm lengths are cancelled out. A QKD system based on this design is currently available for about €100,000 from the University of Geneva spin-out company id Quantique.

At the Toshiba lab in Cambridge, we have developed an alternative compensation technique that allows pulses to be sent just one way, by sending an unmodulated reference pulse along with each signal pulse. These reference pulses are used as a feedback signal to a device that physically stretches the fibre in one of the two arms of the interferometer to compensate for any temperature-induced changes. In trials with the network operator Verizon, the one-way QKD system was continuously operated for over a month without requiring any manual adjustment.

We can assess the performance of QKD systems by the rate at which secure bits can be exchanged. The faster the secure-bit rate, the more frequently the key can be changed, thus inhibiting cryptanalysis. Typical secure-bit rates for complete QKD systems are in the range 10–50 kbit s^–1 for a 20 km fibre link. Although this may seem low compared with the rate data are transferred in optical communications (typically 1–40 Gbit s^–1), it is enough for up to 200 AES encryption keys (each of which comprises 256 bits) to be sent per second – sufficient for most cryptographic applications.

The secure-bit rate that can be achieved decreases with the length of the optical link due to the scattering of photons from the fibre. For this reason, the best performance is usually achieved using photons with a wavelength of 1.55 µm, at which standard optical fibre is most transparent. Even so, when the fibres get so long that the signal rate becomes comparable to the rate of false counts in Bob’s photon detector, sending a secure key is no longer possible. For the standard indium gallium arsenide (InGaAs) semiconductor detectors used to detect 1.55 µm photons, this distance is currently about 120 km. Recently the Los Alamos group has used low-noise superconducting detectors to extend secure key distribution to fibres 150 km in length. Significantly, these distances are long enough for almost all the spans found in today’s fibre networks.

Although the risk of cryptanalysis is mitigated by using QKD to frequently refresh the encryption key, it is not eliminated entirely. However, this can be achieved by encrypting the message using a “one-time pad”, which requires a random key that contains the same number of bits as the message. Each bit of the message is then encrypted by adding it to the corresponding bit in the key using modular arithmetic. Provided that the key distribution is unconditionally secure, as it is using QKD, and that the key is never reused, the one-time pad is completely immune to attack. The downside is the length of the key that must be exchanged. QKD bit rates are already sufficient to allow unconditionally secret voice communication using the one-time pad. In the future, higher bit rates will allow this security to be extended to other forms of data.

Today’s secure-bit rates are limited by how often the InGaAs detectors can detect a photon   currently once every 100 ns. Silicon-based photon detectors can operate almost 1000 times faster, but they are only sensitive to shorter-wavelength photons. As the quality of InGaAs detectors improves over the next few years, we can expect their frequency to catch up with that of silicon, leading to QKD bit rates that are orders of magnitude higher. In the interim, there are encouraging results showing that non-linear crystals may be used to shift 1.55 µm photons to shorter wavelengths for which the faster silicon detectors may be used. Higher detection rates have also been demonstrated using superconducting nanowire detectors, and recent advances with detectors based on quantum dots are also encouraging.

Towards a quantum network

One of the first real-life applications of QKD has been to secure fibre links between corporate sites in a city. Companies are increasingly using high-bandwidth optical connections between offices, data centres, server farms and disaster-recovery sites to obtain the speed and convenience of a local area network over a larger geographical area. In the early days of fibre deployment, immunity to “tapping” of sensitive data was often cited as a key advantage of fibre over copper cable. But in fact, eavesdropping on optical fibres can be accomplished by simply introducing a small bend in the fibre to extract a portion of the light; and, in the absence of quantum cryptography, it is almost impossible to detect.

At Toshiba, we have developed a “link encryptor” that can send data at 1 Gb s^–1 between corporate sites, combining AES data encryption with secure key distribution using one-way QKD (figure 3). Meanwhile, id Quantique announced that it will install its “Vectis” link encryptor between the two centres of data-hosting company IX Europe in Zurich. In the US, MagiQ Technologies has recently developed its own encrypted link, targeted at government applications including the military, intelligence gathering and homeland security.

An important next step will be extending QKD from single point-to-point links into a “quantum network” for key distribution. Networks allow a company to connect multiple sites securely and to add new sites for an incremental cost. Moreover, they allow the range of QKD to be increased from the length of a single fibre link to any distance covered by the network, and safeguard against outages of individual links by automatically routing traffic around them.

In October 2003 BBN Technologies set up a primitive but pioneering QKD network in Cambridge, Massachusetts, linking their site with Harvard and Boston Universities. The firm showed that it was possible to direct the stream of single photons between different receiving units using an optical switch, and it also introduced the idea of “key relay” along a chain of trusted nodes. Here, each pair of adjacent nodes in the chain stores its own local key. A global key may then be sent from one end of the chain to the other, over any distance, by using the local keys and a one-time pad to encrypt each hop.

A more sophisticated system is currently under development by the European SECOQC consortium, a collaboration of academic and industrial QKD researchers, classical cryptographers and telecoms engineers. It is developing the protocols required for routing, storage and management of keys within a meshed network that could in principle be very large. A trial implementation of the quantum net is planned in 2008 that will allow any two users at several sites across Vienna to establish a shared key.

These QKD networks assume that the intermediate nodes are secure, which is realistic if the network is operated by a single service provider. In the future, however, we can relax this condition using a device called a “quantum repeater”. Quantum repeaters are based on the principle of quantum “teleportation”, whereby a quantum state is transferred from one location to another, in principle over an arbitrary distance, using a pair of entangled particles. Recent developments such as a semiconductor device for generating entangled photon pairs and the teleportation of quantum states between photons and atoms bring the quantum repeater closer to becoming a reality.

Meanwhile, an alternative to using a fibre-optic network to send quantum keys over long distance may be to use free-space links to low-orbit communication satellites. In 2006 a collaboration between researchers at the universities of Vienna, Munich and Bristol implemented a free-space link over 144 km between Tenerife and La Palma.

Selling quantum cryptography

From the first laboratory demonstrations over 30 cm of air to the latest fibre-based systems operating over 100 km, QKD has certainly come a long way in the last two decades. The technology has shrunk into compact units the size of typical network equipment and is fully automated. But despite the technical progress there are significant barriers to the adoption of new cryptographic technologies.

A particular problem for QKD is selling technology based on quantum mechanics to clients who often know little about physics and are used to traditional cryptography. Another hurdle is the lack of a security certification process for the equipment. Users need reassurance not only that QKD is theoretically sound, but also that it has been securely implemented by the vendors. It is encouraging that there are several initiatives under way to establish common security standards for QKD.

As the market for QKD develops, we can expect that the price of equipment will drop significantly. Within 10 years we may see QKD used not only in corporate and government networks, but also in networks serving home users. Optical fibres are already used to deliver television, phone and Internet services to domestic users in several countries. Although current QKD systems are too expensive for such applications, they may become viable if miniaturization to microchip-scale and mass-production lead to the expected price reductions. The days when the products of the quantum-information industry serve every household may not be too distant.

The BB84 protocol

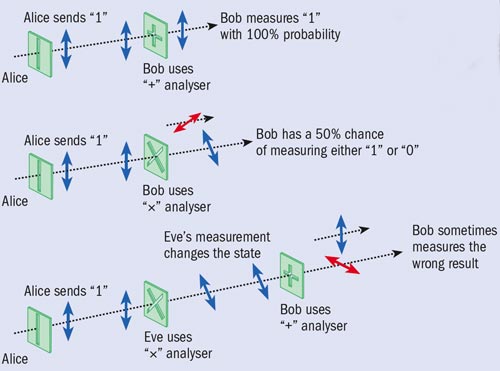
Quantum cryptography is a way of generating a shared secret key that can be used to encrypt and decrypt messages, for example by encoding information in the polarization state of individual photons. In the BB84 protocol, the sender (Alice) transmits photons to the recipient (Bob) in one of four different polarization states: horizontal (H), vertical (V), diagonal (D, 45°) and anti-diagonal (A, –45°). For each photon she sends, Alice randomly selects one of these polarizations, with H or D representing the bit value “0” (red) and V or A representing “1” (blue), depending on the “basis” she chooses. To measure the photons, Bob is equipped with an analyser that can distinguish either between H and V (+) or between A and D (×). He randomly (and independently from Alice) chooses which analyser he will use to measure each photon. If Bob selects the analyser that is compatible with Alice’s choice (top), he will determine the photon’s polarization, and thus the bit value, with certainty. If, on the other hand, Bob measures with the “wrong” analyser (middle), he will obtain a random result.

It seems problematic that half of Bob’s measurements result in a random bit value. However, Alice and Bob have a cunning solution. After Bob’s measurements have taken place, he reveals the sequence of analysers that he used. Alice then tells him which times he used the correct analyser, without revealing the bit that she sent. They can then discard all the measurements for which Bob used the wrong analyser, ensuring that they share the same bit sequence without any errors (in the absence of noise or imperfections).

This post-selection leaves an eavesdropper (Eve) at a disadvantage since she must guess which analyser to use to measure each photon (bottom). Inevitably Eve will sometimes select an analyser that is incompatible with Alice’s choice of polarization, and thus may obtain a result that differs from the bit Alice sent. The key to the secrecy of quantum cryptography is that by making this measurement, Eve inevitably changes the quantum state of the photon. Therefore, when Bob receives the photon, he will sometimes determine an erroneous bit value even when he and Alice used compatible measurements. By examining a small sample of their bit sequence for errors, Alice and Bob can therefore determine whether an eavesdropper was present.

At a Glance: Quantum cryptography

• The quantum states of individual subatomic particles can be used to encode information, opening up applications in communication and computing
• The most mature application of quantum theory to information processing is quantum cryptography, with products already on the market
• Quantum cryptography, also known as quantum key distribution, allows us to send encrypted messages the secrecy of which can be guaranteed by allowing an eavesdropper to be detected
• Secure messages have been sent over distances in excess of 100 km using quantum cryptography with photons carried by optical fibres
• The next step will be to establish a “quantum network” that could allow quantum cryptography to cover cities and eventually the globe

More about: Quantum cryptography

Toshiba Research Europe’s quantum-information group
A wiki for quantum-information research
The SECOQC consortium