Superfluids are among the most peculiar and counterintuitive of all materials. They have no viscosity, which allows an object travelling in a pure superfluid to move without friction. Similarly, they can flow effortlessly through narrow channels and pores that are virtually impermeable to conventional liquids. Superfluids are relatively rare and inaccessible, with only two known examples in liquids: helium-3 and helium-4. Now Peter Toennies and co-workers at the Max Planck Institute of Flow Research in Göttingen and the Russian Academy of Sciences in Moscow have revealed convincing evidence for superfluidity in liquid hydrogen (S Grebenev et al. 2000 Science 289 1532).

The first liquid in which superfluidity was recognized was helium-4 back in 1938. It loses its viscosity below 2.12  K. At the time Fritz London suggested that the phenomenon was associated with Bose-Einstein condensation (BEC), which occurs when an assembly of bosons (particles with zero or integer “spin”) is cooled below a critical temperature. In Bose-Einstein condensation a large fraction of all the particles in the assembly congregate in the zero-momentum ground state.

Superfluidity was later discovered in liquid helium-3, which has a critical temperature of 2.4 mK – about 1000 times smaller than the temperature at which helium-4 becomes a superfluid. Since helium-3 atoms have a half-integer value of spin (i.e. they are fermions), the mechanism behind superfluidity in this system is somewhat different. At the critical temperature, the helium-3 atoms can link up to form Cooper pairs. Because each pair is a boson, the system can then undergo Bose-Einstein condensation like its cousin, liquid helium-4.

Where else might superfluidity exist? The most long-standing example is the electron gas in a superconductor – the original instance of a Cooper-pair system (electrons are fermions). More recently, superfluidity has been observed in laser-cooled alkali gases. Meanwhile, astrophysicists believe that the neutron and proton fluids in neutron stars are superfluid, but this idea is, to say the least, rather difficult to test experimentally.

Although it is generally agreed that there is a close association between Bose-Einstein condensation and superfluidity, the exact relationship has yet to be established. For instance, the ground-state condensate of an ideal Bose-condensed system would clearly not be a superfluid because there is no reason why the atoms should not undergo collisions that would lead to the usual frictional effects. Inter-particle forces evidently play an important role in some way.

Over the years, a great deal of effort has gone into finding new superfluids for experimental investigation. A major difficulty is that materials other than helium solidify long before they have been cooled down to their critical temperature. Even the best candidate, hydrogen, has its triple point at 13.8 K, while the temperature at which Bose-Einstein condensation is predicted to occur is much lower. Hydrogen is therefore already a solid at the temperature at which Bose condensation is expected to take place.

Humphrey Maris of Brown University in the US has explored a possible way to overcome this problem by supercooling the liquid below its normal solidification point – but this has failed. The alternative approach pursued by Toennies and colleagues is radically different.

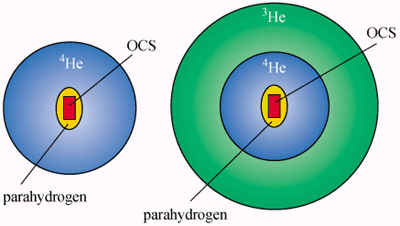
In their experiments at Göttingen, the researchers hold a tiny quantity of “parahydrogen” – a hydrogen molecule in which the proton spins point in opposite directions – within a microscopic helium droplet containing a large impurity molecule, linear carbonyl sulphide or OCS. Each of the droplets contains between 14 and 16 parahydrogen molecules.

In the stable state, the OCS molecule is at the centre of the droplet and is surrounded by a thin layer of hydrogen, which is itself surrounded by a relatively thick shell of liquid helium-4. It is also possible to add an outer shell of liquid helium-3 (figure 1).

The droplets cool almost instantly by evaporation as they enter a vacuum region in the apparatus through a nozzle a few microns wide. Those with a helium-4 outer shell reach 0.38 K, while the helium-3-coated droplets cool to 0.15 K. In both cases, the helium-4 shell has to be a pure superfluid with no viscous “grip” on the rest of the droplet.

The drops are analysed using an infrared laser as they travel from the source to a quadrupole mass spectrometer. The detector signal decreases markedly when the wavelength of the laser is tuned so that the droplets readily absorb the photons. A variety of different modes of the OCS molecule can, in principle, be excited. Of particular interest are the rotational states of the OCS-parahydrogen complex. If the complex rotates as a whole, it has a relatively large moment of inertia. However, if the parahydrogen layer becomes superfluid, it largely decouples from the OCS, so that its net moment of inertia falls to almost zero.

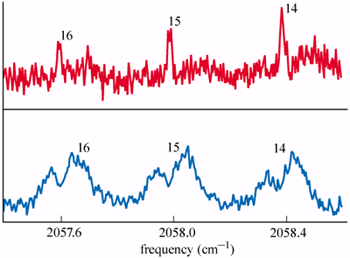
Examples of the spectra obtained using the two types of droplets at different temperatures are shown in figure 2. In each case, the spectra are almost identical for droplets containing different numbers of parahydrogen molecules. However, the shapes of the spectra at the two temperatures are totally different. The sharp peaks at 0.38 K are related to rotation of the complex, and their absence at 0.15 K strongly suggests that rotation is no longer being excited. The most likely explanation is that the moment of inertia of the OCS-parahydrogen complex has fallen to a very small value at 0.15 K because the onset of superfluidity in the hydrogen at some temperature between 0.38 K and 0.15 K has caused it to decouple from the OCS.

When the experiment was repeated with deuterium in place of the hydrogen, the sharp peaks still persisted at 0.15 K, indicating an absence of superfluidity in deuterium at this temperature. Toennies and co-workers have carried out several checks and simulations, and all of these seem to confirm the central conclusion that parahydrogen is a superfluid at 0.15 K.

How does this result relate to more conventional types of experiment? It should be emphasized that superfluidity in a shell containing about 15 hydrogen molecules does not necessarily mean that the phenomenon will ever be observed in bulk liquid. Indeed, it probably will not, due to the difficulty of maintaining the liquid state at low enough temperatures. But the results for droplets seem to have given us a new superfluid, presumably quite different from the liquid heliums with which low-temperature physicists are so familiar. It will be an interesting challenge to find ways of studying superfluid parahydrogen in order to establish its properties.