Scholars have long debated whether the Sagas of Icelanders – ancient narratives set in the Viking Age – are fact or fiction. Ralph Kenna and Pádraig Mac Carron analysed the structures of the saga societies to shed light on this question

The Sagas of Icelanders are prose narratives purporting to describe events during the settlement of Iceland more than 1000 years ago. Njáls saga is the most extensive of the Íslendinga sögur, and is often seen as the greatest piece of Viking Age Icelandic literature. The protagonist is Njál Thorgeirsson, a sage and lawyer. He and the warrior-chieftain Gunnar Hámundarson are close friends and Njál’s outstanding wisdom is complemented by Gunnar’s extraordinary physical prowess. When Gunnar marries the beautiful Hallgerthr, however, things go awry. Hallgerthr instigates a feud with Njál’s wife Bergthóra and minor insults and provocations ensue, escalating to major incidents of bloodshed in which scores of characters, including both Gunnar and Njál, die.
The antiquity of these anonymous texts and their narrative style make them unique in world literature. As with other ancient narratives, however, their historical authenticity has for many years been subject to scholarly debate. Some believe they contain descriptions of real Viking life and society. Others object that they are fictional and without any historical value.
Since these are questions of historical and literary merit, you might be wondering what physicists can possibly have to say about something that is seemingly so far removed from their own field. Statistical physicists, however, have always been interested in applying their wares outside the confines of physical systems. The subject itself emerged from probability theory in the 19th century, in parallel with the development of sociology – an early term for which was “social physics”. Nowadays sociophysics has re-emerged as a distinct branch of physics, drawing especially from statistical physics. The latter deals with collective phenomena in materials that emerge when lots of simple particles interact; an individual water molecule, for example, cannot freeze or flow but a huge collection of them can. Similarly, some properties of a population may not be simple aggregates of those of individuals. Examples include co-operative behaviour: a single bee cannot swarm and a single physicist does not have the critical mass of a research group.
In our research we take a step further and go beyond the interactions between particles and even beyond people we know to be real. Instead, we consider relationships between large casts of characters in epic texts and sagas. Viewing these as complex systems, we can use techniques from statistical physics to characterize these societies, ultimately exploring whether the communities they describe are credible.
Examining Njál’s world
The temptation to regard epic and saga narratives as treasure troves of data susceptible to the tools of statistical physics became irresistible when we realized that the field of “comparative mythology”, where scholars study myths from different cultures, has a concept familiar to all physicists who have worked with critical phenomena. Critical phenomena occur near the boundary between two or more physical phases, such as the “critical point” at which coffee starts to percolate or the “Curie temperature” at which certain materials lose their permanent magnetic properties to transition between ferromagnetic and paramagnetic phases. The familiar concept that is found in both critical phenomena and comparative mythology is universality.
Universality is where different systems have the same macroscopic properties, independent of details, of what the system is made of or how it is put together. In statistical physics, the essential behaviour of such systems – be they physical or social – can be described using just a few numbers, without referring to the specific details of the constituent parts, such as the single coffee grains or the individual people. These few universal parameters include critical exponents, so-called because in formulae describing phase transitions, they are the powers to which control parameters are raised. The values of the critical exponents can then be used to categorize the phase transitions.

In comparative mythology, universality is a relevant notion – though it has only been qualitative until now. One example is narratives that are claimed to have a common structure known as the monomyth, in which a hero goes on an adventure, has a crisis, wins a victory and then returns home transformed. Although the original concept of the monomyth has somewhat fallen out of favour, we considered whether we can introduce a new measure of universality – something different, and more akin to classifying phase transitions in statistical physics – whereby narratives are quantified so that they can be measurably compared.
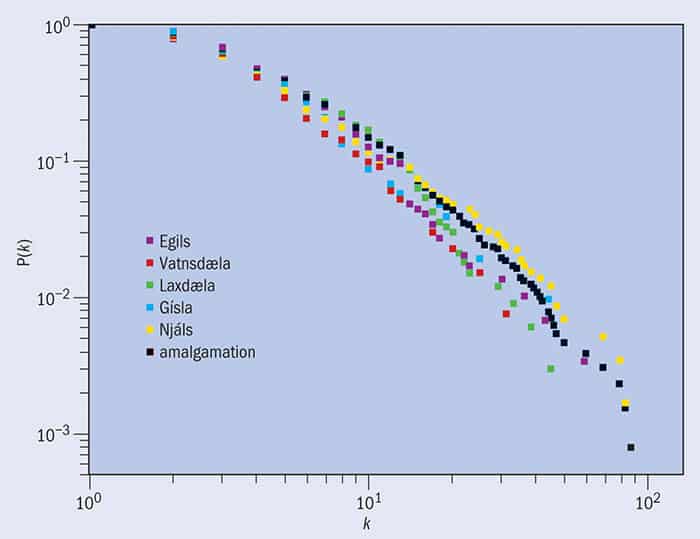
To do this we constructed social networks from the Íslendinga sögur (2013 Eur. Phys. J. B 86 407). Our tasks involved identifying characters in the sagas and defining the relationship each has with others. Njáls saga, for example, involves 575 “nodes” (characters) linked by 1612 “edges” (interactions or relationships). It is depicted in figure 1, where positive (friendly) relationships are represented in blue and negative (hostile) ones are in red. The “degree” of a node is the number of edges attached to it, which means that someone who knows a lot of people corresponds to a high-degree node, and someone who knows hardly anyone is represented by a low-degree node. For Njáls saga, a plot of the number of people against the degree each person has is well described by a power law, in which many people have only a small number of acquaintances, while a few people have a lot (see figure 4). Omnipresent in physics, such power-law distributions lack an intrinsic scale and are “fat-tailed” compared with, for example, the normal distribution, meaning that a few nodes can have very high degrees.
In modern society, the familiar “six degrees of separation” concept quantifies the fact that everyone can be linked to everyone else in the world by a remarkably short chain of friendships. For the character network underlying Njáls saga, we found that the equivalent average number of steps between people, or “mean path length”, is even less: about five. Another way to describe a social network is to quantify the amount of “clustering”. In most real-world networks, a high proportion of one’s acquaintances are also acquainted with each other. When viewed as a network map, this appears as clusters of tightly bound groups of nodes, as opposed to nodes that are uniformly spread out. In a social network with lots of positive interactions, clustering tends to be high. With both its short path length and high clustering, Njáls saga is called a “small world”.
Experience shows it is difficult to stay friends with two acquaintances who are mutually hostile. In network terms, a single negative link in a relationship triangle between three people (A, B and C) is rare because if A and B don’t like each other, it prompts the other node (C) to take sides. Similarly, triangles comprising three hostile relationships are also rare; realizing that “the enemy of an enemy is a friend” prompts two nodes to gang up on the third. The propensity to disfavour odd numbers of hostile links in a relationship triangle, which is known as “structural balance”, is evident in saga society. In Njáls saga, for example, only 10% of triangles have an odd number of hostile links.
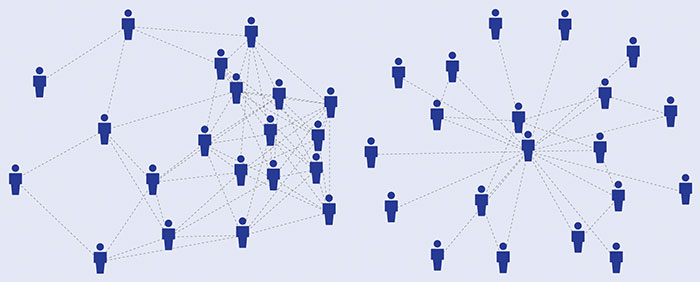
In real life, people tend to associate with other people who are similar to themselves. Popular people, for example, tend to be mutually acquainted, while friends of less popular people also tend to be less popular. In network science, this is called “assortativity”. Its opposite – popular people interacting with unpopular people – is called “disassortativity” and both are illustrated in figure 2. The extent to which a network is assortative or disassortative can be quantified using a measure of the correlation between the degrees of the nodes known as the Pearson’s coefficient, which is positive for assortativity, and negative for disassortativity. Real social networks tend to be assortative and we find it is marginally so for Njáls saga. Another level of analysis we can use is to look at the positive-interaction networks only, since these are better able to capture the complexity of social networks than negative interactions, which have topologically trivial structures. Njáls saga is even more assortative if negative relations are excluded.

We conclude that the society described in Njáls saga is a highly clustered, structurally balanced, assortative small world with a fat-tailed degree distribution. While each of these characteristics is not unique to social networks, together they are characteristic of them. Though we cannot prove whether Njáls saga is fact or fiction, we can say that the network structure of the society underlying the tale is realistic.
The bigger saga picture
What about the other narratives from the Icelandic collection? We examined a further 17, four of which – Vatnsdæla, Laxdæla, Egils and Gísla saga – are particularly susceptible to network analysis, which works best when applied to large casts. The saga of the people of Vatnsdæla describes how the grandson of a Norwegian chieftain came to Iceland, then follows his family until the arrival of Christianity in the 10th century. The saga of the people of Laxdæla, meanwhile, has the second-largest network after Njáls saga. Like Njáls and Vatnsdæla, it is a family saga and some believe the author of Njáls saga may have used Laxdæla as a source. As for Egils saga, it also starts off in Norway, from which Egil’s family flees to Iceland, following a dispute with the king. Although a family saga, it centres on the life of Egil, a poet, farmer and warrior who gains our sympathies only to lose them again through his excessive violence. Gísla saga differs from the others in that it is an outlaw saga, in which the eponymous character is on the run for 13 years before finally being killed.

We found that these five sagas have certain statistics in common: each of them is a highly clustered, structurally balanced, small world. They are well described by power laws with similar exponents, although Laxdæla is better fitted by an exponential distribution. Where they differ from each other is in their assortativity. The family sagas Njáls, Vatnsdæla and Laxdæla are assortative. Egils saga is mildly disassortative but if we confine our analysis to its positive relations, that too has assortativity close to zero. As for Gísla saga, it is the only one which is centred on the exploits of a single individual rather than on a society, and this is reflected in the fact that it is the only one of the five sagas for which the overall network is disassortative, and strongly so at that.
Apart from their narrative style being so consistent and objective, a fascinating feature of the Íslendinga sögur is that they contain interwoven and overlapping plots, whereby main characters in one text can appear as minor ones in another. The merger of the five major sagas is depicted in figure 3. The social networks of three of the sagas – Vatnsdæla, Egils and Gísla – are fairly distinct. However the communities in two of the sagas – Njáls and Laxdæla – strongly overlap, which may be interpreted as supporting the theory that one may have been used as a source for the other. All five are well described by power laws similar to that exhibited by Njáls saga (figure 4).
Combined, the 18 sagas form a huge network that is a structurally balanced, assortative small world. Its mean path length of 5.5 is remarkably close to the six degrees of separation of modern society. Its degree distribution is best described by a truncated power law, the cut-off being due to the fact that no single protagonist appears as a major player in multiple sagas.
So our physics-inspired investigations of saga society, we have focused on the totality of relationships between the characters depicted in the texts, rather than on the characters themselves, as most humanities researchers have done. This approach brings to the fore the credibility of the societal backgrounds in the sagas. Even if some of the events are fictional, they may play out against a backdrop that includes real history.
Our investigations are an example of curiosity-driven research and demonstrate how ideas inspired from physics can help other fields of inquiry. Obviously, our conclusions are from a network-science standpoint and input from other fields – archaeology, literature and comparative mythology – are required for an overall view. Nonetheless, we can conclude that, historically accurate or not, the societies recorded in the Íslendinga sögur are similar to those of modern social networks and as such are remarkably realistic.
Greek, Anglo-Saxon and Irish epics

Our analysis of the Íslendinga sögur forms part of a broader initiative called Maths Meets Myths involving world epic literature and funded by the Leverhulme Trust, the European Science Foundation and the European Commission. In this context, we also examined narratives from Greece, Britain and Ireland (2016 J. Phys.: Conf. Ser. 681 012002; 2012 EPL 99 28002) and it is interesting to view the Icelandic sagas in these contexts.
Homer’s Iliad, penned in Ancient Greece, is considered as one of the markers of the beginning of the Western canon. Some evidence suggests that it may be based on historical conflict during the 12th century BC. Beowulf is an Anglo-Saxon epic, set in Scandinavia. Although embellished by obvious fiction, archaeological excavations support historical authenticity associated with some of its human characters. As for the Táin Bó Cúailnge, it is an Irish epic that some argue corroborates Greek and Roman accounts of the Celts, offering a “window on the Iron Age”. But others say that tales such as these three have no historical basis whatsoever. More think that they reflect the times of the medieval scribes who recorded them rather than the societies in which the stories are supposed to be set.
We find that the networks in Njáls saga and the combined Íslendinga sögur are more similar to that of the Iliad than they are to either the Irish or Anglo-Saxon texts. One important difference between the Icelandic texts and the Iliad, however, is that while the full saga network is “assortative”, that of the Iliad is not. To render the networks more alike, one would have to restrict to positive interactions in the Iliad network, which is then assortative. In other words, the Íslendinga sögur have similar network properties to the Iliad when hostility is removed from the latter but are quite different from Irish and Old English epics. Of all the epic literature we examined so far, the sagas of Iceland are the most realistic. Finally, although it is believed that Tolkien was influenced by Nordic literature, The Lord of the Rings and many other works of fiction have very different network structures from those of saga society.



