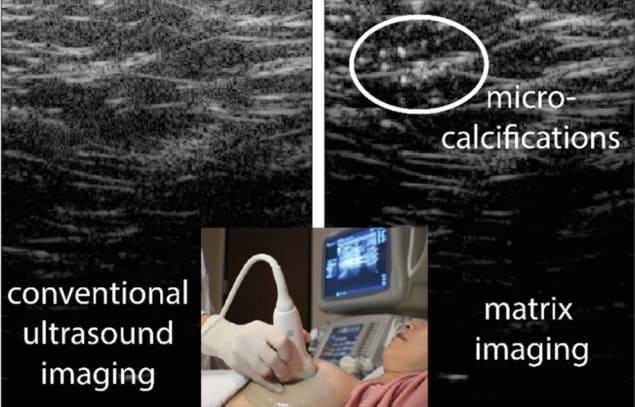
Ultrasound imaging uses the reflection of waves to image soft tissues within the body. However, soft tissues have inherent inhomogeneities that can distort the incident and reflected propagating waves. Consequently, wave speed fluctuations and multiple scattering events lead to inevitable blur in the resulting images. To resolve this problem of image quality degradation, researchers have employed the adaptive focusing approach, which can compensate for image distortions caused by uneven interfaces or tissue inhomogeneities.
Conventional adaptive focusing methods are based on a dominant scatterer – an artificial reference point from which the signal to be optimized is reflected. However, it is not always straightforward to generate a reference point that accounts for all the imperfections of a heterogeneous medium. In addition, conventional adaptive focusing methods that correct for aberrations to optimize the image quality are often based on the assumption that these aberrations do not change over the entire field-of-view. In reality, the extent of image distortions can vary as a function of imaging depth inside a biological tissue.
To overcome these limits for ultrasound imaging, several acoustic imaging groups have developed methods to estimate and compensate for the time delays of emitted and reflected signals (as sound waves travel through different tissue depths) and mapped the speed-of-sound distribution to enable reconstruction of an image. But a more general approach that could be extended to any type of wave was not previously available. Now, researchers at the Institut Langevin (ESPCI Paris, PSL University, CNRS), led by Alexandre Aubry, have developed a universal matrix approach for wave imaging, using a multi-sensor network.
In collaboration with SuperSonic Imagine, the researchers published their imaging method – a reflection matrix approach for quantitative imaging of scattering media – in Physical Review X in early June. A week later, they published the experimental proof-of-principle of their theoretical results in PNAS. In this latter study, the researchers showed that their mathematical formalism can correct for aberrations that are inevitably present in in vivo images of the human body.

A novel approach
The novelty of the team’s work is that, unlike adaptive focusing methods, the reflection matrix approach is not limited to a single isoplanatic patch (area over which aberrations are spatially invariant). Instead, their approach retrieves the transmission matrix which connects any point inside the tissue with an array of external ultrasound sensors, to tackle more rigorously the challenges induced by random scattering media in medical ultrasound applications.
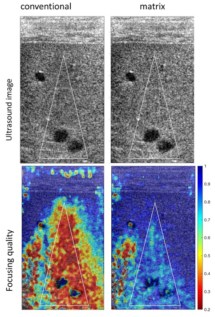
This new technique records the amplitude and phase of the tissue response, i.e., the ultrasound signal reflected from the tissue. Then, by using a position-dependent matrix, elements corresponding to the angle of rotation of the imaging plane and signals emitted/reflected by each transducer in the array can be accessed to link each sensor and image voxel.
As a random distribution of unresolved scatterers makes adaptive focusing more challenging, the reflection matrix approach considers the reflectivity of the medium to be continuous and random. Thus, the reflection matrix can be projected to each isoplanatic patch separately and therefore distinguish and resolve aberrations in multiple fields-of-view.
Finally, the team applied their aberration correction technique to ultrasonic data recorded from the calf of a healthy human volunteer. This in vivo imaging experiment confirmed that the distortion matrix approach can be extended to cases in which the speed-of-sound distribution in the medium is unknown, as the matrix can correct for complex position-dependent distortions.
The researchers tested and confirmed their theoretical developments using one particular type of wave. However, they believe that the potential of this work goes beyond ultrasound imaging as it can be applied to all fields of wave physics. Aubry notes that his group’s work on broadening the application of the distortion matrix approach to optical microscopy will shortly be published in Science Advances.