Gamma ray detectors used in positron emission tomography (PET) scanners must combine high spatial, timing and energy resolution with excellent sensitivity. Current clinical PET scanners employ pixelated scintillation detectors with a spatial resolution limited by their pixel size. Another option is to use a monolithic crystal detector, read out by a photodetector array, which offers increased sensitivity and resolution. Already implemented in preclinical PET systems, such monolithic detectors may soon also appear in clinical scanners.
Monolithic PET detectors, however, bring their own challenges, such as a lengthy calibration setup and edge effects. Another key task when using a monolithic detector is to design an efficient and accurate gamma event positioning algorithm, with limited degradation in performance towards the edges of the crystal. To achieve this, researchers at Ghent University have used artificial neural networks to create a high-resolution gamma positioning algorithm. They describe their study in Physics in Medicine & Biology.
“We chose to investigate neural networks as they can be trained to directly infer the continuous interaction position from the measured light distribution, based on example data,” explains first author Milan Decuyper. “They can learn to optimally process events near the edges and, once trained, positioning events is fast and parallelizable.”

Network optimization
PET scanners work by detecting the pair of 511 keV gamma rays produced when a positron emitted by a radiotracer annihilates with an electron. Forming a line-of-response between the pair enables localization of their source. However, some of the gamma rays undergo Compton interactions within the crystal before the final photoelectric interaction, making recovery of the first interaction position more difficult.
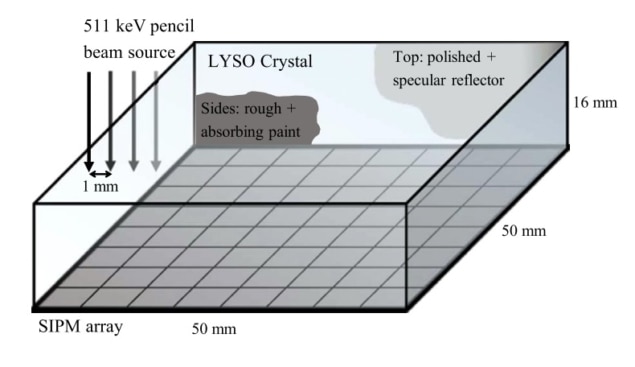
Decuyper and colleagues trained a neural network to learn the mapping between the measured light distribution and the first (Compton or photoelectric) interaction position in a monolithic crystal. For their study, they simulated a 50×50×16 mm LYSO (Lu1.8Y0.2SiO5) crystal, irradiated with a 511 eV source and read out by an array of photodetectors.
The researchers simulated a training dataset that covered the detector in 1 mm steps, with 10,000 training events and 2000 evaluation events per position. In the simulation, around 60% of events were Compton scattered. They also created an independent “overfitting” dataset in the detector centre, using grid points offset by 0.5 mm from the training grid.
To assess performance as a function of network complexity, the team examined networks with two to five hidden layers and 64 to 1024 neurons in each layer. When evaluated using data from the same grid as the network was trained on, the most complex network gave the best performance. However, when evaluating intermediate positions that were not part of the training dataset, the researchers saw that performance degraded with more complex networks. They point out that this illustrates the potential pitfall of overfitting.
The team also assessed performance as a function of the amount of training data. The positioning error significantly reduced as training events per calibration position increased from 100 to 1000, and then levelled off. Optimal performance was achieved with a network containing three hidden layers of 256 neurons trained on 1000 events per position.
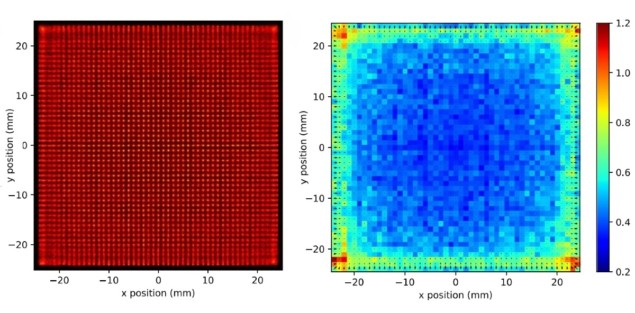
Over the entire detector, this optimal network achieved mean and median spatial resolutions (the 2D FWHM of the predicted position) of 0.50 and 0.46 mm, respectively. The distance between the ground-truth and the predicted position was 1.1 mm on average, with a median of 0.50 mm. In the central 30×30 mm region, the spatial resolution improved to 0.41 mm, with equivalent positioning accuracy.
Comparing the performance of the neural network with that of a nearest neighbour algorithm approach that the team developed previously demonstrated that 0.46 mm represents a 17% improvement in spatial resolution over nearest neighbour positioning.
Extension to three dimensions
Another benefit of monolithic detectors is that they offer intrinsic depth-of-interaction (DOI) information, which can improve the timing resolution. The team extended the neural network to output the estimated DOI (an additional z coordinate). This gave similar performance to the 2D positioning network, with almost no impact upon the spatial resolution. The mean and median 3D positioning errors were 1.53 and 0.77 mm, and the mean and median DOI errors were 0.87 and 0.39 mm, respectively.
Investigating the influence of Compton scatter revealed that it considerably reduced positioning accuracy, with the mean positioning error increasing from 0.49 for non-scattered events to 2.29 mm for Compton scattered events. Compton scatter also degraded the spatial resolution, with median values of 0.66 and 0.42 mm FWHM for scattered and non-scattered events, respectively.

β-CUBE delivers high-performance small-animal PET
While identifying and removing Compton events could improve image quality, it would also considerably decrease sensitivity. A better approach, the team suggests, may be to train neural networks to identify Compton scattered events and process them differently.
The researchers conclude that neural networks can perform 3D gamma ray positioning with very high spatial resolution, superior to previous approaches. They are now evaluating their experimental PET detector using the same configuration as in the simulation setup. “This allows us to see how our methods and results based on simulation data transfer to experimental data,” Decuyper tells Physics World.



