The discovery that neutrinos have mass and can oscillate between different flavours was one of the major breakthroughs in particle physics in the past decade, but there is much about these mysterious particles that we still do not understand

The world of neutrino physics has come a long way in the last 30 years. Once a ghostly afterthought of particle physicists, introduced to explain something that was missing rather than something that was there, neutrinos have proved to be every bit as fascinating as quarks, gluons and all the other fundamental particles. Indeed, they might even be able to explain one of the biggest puzzles in physics: where did the matter in the universe come from?
According to the Big Bang model, the universe began 13.7 billion years ago as a tiny region of pure energy that expanded and cooled to create the cosmos we see today. Among the many successes of this model, however, there is at least one glaring problem: the universe is dominated by matter and contains very little antimatter. The laws of physics do allow energy to be converted into matter, but require that almost equal quantities of antimatter are produced in the process.
It is now becoming clear that the answer to this puzzle could come from a very unexpected quarter: the behaviour of neutrinos. How we have come to this startling conclusion is a fascinating tale and, as is so often the case in science, the story begins with a completely different problem.
The birth of the neutrino
The concept of neutrinos dates back to the 1930s, when researchers noted that energy seemed to disappear when one atomic nucleus decayed into another nucleus plus an electron. Wolfgang Pauli hit upon a “desperate remedy” to explain the situation, proposing that the missing energy was being carried away by a third particle emitted in the decay. To the modern reader this might not seem particularly revolutionary, but in Pauli’s day there were only two known particles – the electron and the proton – so introducing a third particle was radical in the extreme.
Understandably Pauli was initially reluctant to publish the idea, and even apologized afterwards for predicting a particle that he thought would be impossible to detect (if only modern theorists were similarly concerned!). This was because his “neutrinos”, as Enrico Fermi christened them, had no electric charge and would interact only weakly with other matter. Happily, Pauli was proved wrong and lived to witness the Nobel-prize-winning detection of neutrinos in 1953 by the late Fred Reines and Clyde Cowan.
But the emerging field of particle physics did not, of course, end there. We went on to discover the positron (anti-electron), the pion, the muon and many other novel particles. Along with the muon came another neutrino, now called the muon neutrino, νμ, which was found to be distinct from the electron neutrino proposed by Pauli (νe). Then, after the discovery of the tau lepton in 1975, it was apparent that there was a third “flavour” of neutrino: the tau neutrino, ντ, which was finally detected in 2000 by the DONUT experiment at Fermilab in the US.
Meanwhile, the plethora of strongly interacting particles such as protons and pions was brought into order by the quark model. Combined with a handful of other particles that could explain the forces between elementary particles, this left us with a rather simple but extremely powerful picture of particle physics called the Standard Model. In this model, neutrinos were initially considered to be strictly massless and to interact only via the weak interaction though the exchange of the “Z” and the “W” particles. Reality, however, has turned out to be somewhat more complicated than this.
A problem with the Sun
In the 1960s, while other particle physicists were investigating all these newly discovered particles, Ray Davis at the Brookhaven National Laboratory in the US was pursuing the idea of using neutrinos as a probe. For decades astronomers had thought that the most likely power source for the Sun and other stars was thermonuclear fusion, but no direct proof was available. Davis believed he could observe the fusion reactions directly by detecting the neutrinos they produced.
In the basic fusion reactions in the Sun, four protons are converted into a helium-4 nucleus, emitting two positrons and two electron neutrinos in the process. These neutrinos have a wide range of energies and vast numbers of them escape from the Sun without interacting with anything, hurtling towards the Earth at close to the speed of light. But it is precisely this extremely low probability of interacting with matter that makes neutrinos so hard to detect.
Davis tackled this problem using a technique from radiochemistry proposed by Bruno Pontecorvo while at the Chalk River Laboratory, Canada, in 1946: assemble a large mass of some target atom that will very occasionally undergo a nuclear reaction triggered by a solar neutrino. Davis chose an isotope of chlorine as the target, which he managed to obtain at an acceptable cost in the form of 600,000 litres of cleaning fluid. Neutrinos from the Sun would then react with the chlorine to produce radioactive argon atoms, which could be “gathered up” and individually counted. Knowing the probability that a neutrino would trigger the reaction in the first place, it would then be possible to infer the solar-neutrino flux.
The first results of this audacious experiment were announced in 1968, and surprised almost everyone. Davis’ team only detected about 30% of the neutrinos predicted by the best solar models available, namely those developed by John Bahcall and colleagues. At first, researchers were sceptical as to whether a few atoms of argon could really be seen in such a huge volume of liquid, but after rigorous tests it seemed the experiment was not at fault. Nevertheless, the real proof that the “solar-neutrino problem” was here to stay did not come until twenty years later, when the Kamiokande experiment in Japan confirmed Davis’ results. Davis and Kamiokande spokesperson Masatoshi Koshiba of the University of Tokyo shared the 2002 Nobel Prize for Physics for their pioneering work in neutrino astrophysics.
The Kamiokande experiment consisted of several thousand tonnes of pure water in a tank deep underground, and was originally built to search for proton decay. However, its designers realized that the experiment might also be able to detect highly energetic neutrinos from the Sun that interact with electrons via scattering reactions. These electrons can travel faster than the local speed of light in the water, causing them to emit the optical equivalent of a sonic boom – a glow of blue light called Cerenkov radiation that can be detected by ultra-sensitive photomultiplier tubes around the tank.
In 1989 the Kamiokande team confirmed that the flux of neutrinos from the Sun was indeed much lower than expected. But experimental particle physicists take a lot of convincing, and there was still the possibility that the solar-neutrino problem arose not from the neutrinos but from the solar models themselves. This is because the neutrino flux measured by the Davis and the Kamiokande experiments was dominated by high-energy neutrinos from a small side reaction involving the decay of boron-8. The rate of this reaction depends critically on the core temperature of the Sun, so a small error in this temperature could explain the low neutrino fluxes seen in both experiments. We therefore had to confirm that all solar neutrinos were suppressed, not just those at high energies.
This required two new experiments called SAGE and GALLEX, which followed the basic idea of Davis’ experiment except that they used gallium instead of chlorine as the target atom. Due to the more complex chemistry involved, these experiments were more difficult to perform, but in the early 1990s we eventually got the answer: the low-energy neutrinos were missing too. The problem did not lie with the solar models – it was something else.
Neutrino oscillations
If neither the solar models nor the experiments were at fault, then what was the source of the solar-neutrino problem? One solution, which was actually proposed by Pontecorvo the year before Davis had obtained his first results, was that neutrinos may change from one flavour to another on their journey from the Sun to the Earth (see box 1 below). Since the existing experiments were predominantly sensitive to electron neutrinos, rather than muon and tau neutrinos, this could explain why we only detected about a third of the solar neutrinos.
But there was one big problem with this neutrino-oscillation idea: it requires that neutrinos have mass, which they do not in the Standard Model. At the time this was an exciting prospect because it meant that neutrinos might explain the “dark matter” that is thought to dominate the universe. We now know that neutrino masses are too small to account for most of this strange, non-luminous substance (even so, there is roughly the same amount of mass in neutrinos as there is in all the visible matter in the universe). But these tiny neutrino masses are still of great interest because they might arise from some fundamentally different mechanism to the way the masses of other particles are generated – i.e. the Higgs mechanism.
The theory of neutrino oscillation contains a few underlying parameters: the masses of the three neutrino states ν1, ν2, and ν3 (see box 1 below) or rather the two independent differences between them, Δm122 and Δm232; three “mixing angles”, θ12, θ23 and θ13; and a critical parameter called the phase, δ. Measuring this phase could be one of the keys to answering the riddle of why the universe contains more matter than antimatter. But before physicists could explore this possibility, we still had to determine whether neutrino oscillations were simply nice mathematics or real physics. In particular, we needed to measure the mass differences and mixing angles.
While proof of neutrino oscillations was being sought, a separate problem began to unfold in experiments searching for proton decay. Proton decay may or may not take place, but it is certainly very rare (the lifetime of the proton is predicted to be at least 1032 years). Experimenters have therefore had to worry about other processes that might hide or even mimic the decay of a proton in their detectors.
The largest source of such background events are neutrinos from cosmic rays, the high-energy particles that constantly bombard the Earth’s atmosphere from sources in our galaxy and beyond. The debris of these collisions is dominated by pions, which decay into muons plus muon neutrinos in reactions such as π– → μ– + νbarμ, where the horizontal bar depicts a antineutrino. The muons themselves then decay into electrons and more neutrinos via the reaction μ– → e– + νbare + νμ.
This process should therefore produce two “atmospheric” muon-neutrino events for every electron-neutrino event. However, to the surprise of researchers working on a Kamiokande-like detector called the Irvine Michigan Brookhaven (IMB) experiment, and of the Kamiokande team itself, this ratio was not seen. Instead, the two experiments saw roughly the same number of both types of neutrino. As with the solar-neutrino problem, many physicists initially thought that this “atmospheric-neutrino anomaly” was simply due to a problem with the experiments, or possibly the models of atmospheric-neutrino generation. However, in 1998 a vastly larger version of Kamiokande called SuperKamiokande convinced almost everyone that the atmospheric anomaly must lie with the neutrinos themselves.
The breakthrough came because SuperK was able to compare the events that came “down” from the atmosphere with events that came “up” from below, and hence arose from interactions in the atmosphere on the other side of the planet (figure 1). The only significant difference between these two classes of neutrino is the distance they have travelled, but if neutrinos are massless this should make no difference.
However, for events coming from above, SuperK saw roughly the expected 2:1 ratio of muon to electron neutrinos, while for events coming from below it saw many fewer muon neutrinos. This was subsequently confirmed by the Soudan II and MACRO experiments, and demonstrated that nature really does satisfy the first condition for neutrino oscillations: that neutrinos have mass. But what about the second condition, that neutrinos change flavour?
Solving the solar-neutrino problem: SNO and KamLAND
Demonstrating that neutrinos can change flavour was the main purpose of the Sudbury Neutrino Observatory (SNO) in Canada, which was built by a large collaboration of Canadian, US and UK physicists (and which I have been a part of since 1988). SNO is a water Cerenkov detector like Kamiokande, but instead of using normal water it uses heavy water, D2O. The deuterons, D, in the heavy water are the most weakly bound of all nuclei, which gives SNO the chance to observe three different reactions induced by solar neutrinos.
The first of these processes is the charged-current reaction νe + D → p + p + e–, which is detected by observing Cerenkov photons from the energetic recoil electron, e–. This reaction is only sensitive to electron neutrinos, which is good because these are the only type produced by nuclear reactions in the Sun’s core. But what happens if these neutrinos oscillate on their way from the Sun to the Earth?
This is where the second reaction, the neutral-current reaction νχ + D → p + n + νχ, comes into play. This is observed via the emitted neutrons, n, and is independent of the flavour of the incoming neutrino, χ. It therefore provides a way to normalize the total flux of neutrinos being emitted by the Sun. In the absence of neutrino oscillations, the flux inferred from the charged-current and neutral-current reactions would be the same, while neutrino oscillations would lower the charged-current rate but not the neutral-current rate. As a result, SNO can determine whether or not neutrinos change flavour regardless of the details of solar models. The third interaction is the same electron-scattering reaction already observed by the two Kamiokande detectors, νχ + e– → νχ + e–, which has some sensitivity to all neutrino flavours but does not allow a clean comparison between them.
Building an experiment like SNO is no simple task. First, you need 1000 tonnes of heavy water, which is not generally found at your local hardware store. Luckily, Ontario Hydro uses large quantities of heavy water in its nuclear reactors and was willing to lend us one reactor’s worth on the condition that we give it back (it is worth hundreds of millions of dollars). Then you need to dig an enormous cavity at great depth in which to house your detector. Again, tremendous good fortune led us to the INCO nickel-mining company, which has been supernaturally tolerant of a bunch of physicists doing rather odd things in its extremely profitable mine. Finally, once you have secured many millions of dollars to fund all of this, you get to the hard part: building the detector itself.
The difficulty arises because of natural background reactions that can mimic neutrino signals. Gamma rays arising from the radioactive decay of ubiquitous uranium and thorium are a particular problem, as they can break up deuterons and release neutrons that cannot be distinguished from those produced by neutral-current reactions. The only way to control this background is to build the detector from specially selected materials in a giant cleanroom – a cleanroom 2 km underground in an active and very dirty mine.
Once all this was accomplished in 1999 the fun really began, because the detector does not just say, “Hey, there was a neutrino – add one to the charged-current list!” The problem is that you cannot directly measure the response of the detector in order to pick out the few – about 10 per day – solar-neutrino events from the tens of events per second coming from background processes. Instead, we had to laboriously understand the behaviour of the detector from first principles using optical and radioactive sources, and computer simulations. Once this effort was complete, actually fitting the neutrino signals was relatively straightforward.
The results, announced in 2001 and 2002, confirmed beautifully the neutrino-oscillation prediction. The number of neutral-current events matched the predictions of the solar models quite precisely, showing that the total neutrino flux is actually spot on. However, the charge-current reaction rate showed that only about a third of these neutrinos are electron neutrinos by the time they reach the Earth, which proved that neutrinos change flavour on the way.
In 2004 we improved this measurement by adding two tonnes of salt to the heavy water, which makes the neutrons from the neutral-current events much easier to detect. But just to be absolutely sure that solar neutrinos really do change flavour, we are now repeating the experiment yet again. This time, however, we will be able to detect the neutral-current events independently of the charged-current events using an array of very sensitive neutron detectors. This will make the detector more sensitive to the mixing between electron- and muon-type neutrinos (and hence improve the measurement of the angle θ12), while at the same time making extra sure that we have not been fooled by our first two measurements.
So, SuperKamiokande’s atmospheric-neutrino results from 1998 showed that neutrinos have mass, while, a few years later, SNO showed that neutrinos can change flavour. Does this prove that neutrino oscillations occur? Well, not quite, because a number of other models have been proposed that can also explain these data, ranging from new neutrino properties to the effects of higher dimensions. Luckily, in 1994 another Japanese group had proposed a very clever experiment called KamLAND, which provided the final piece of evidence for neutrino oscillations.
KamLAND is a large detector built in the old Kamiokande cavity that takes advantage of Japan’s nuclear reactors, which are powerful sources of electron antineutrinos (some 30% of Japan’s energy comes from nuclear power stations). Coincidentally, these reactors are at the right distance away for neutrino physics: close enough for their antineutrinos to be detected, but far enough away that neutrino oscillations should significantly suppress the number of electron antineutrinos detected.
The most recent results from KamLAND, reported last summer, clearly show not only a suppression of the detected flux, but also a distortion of the spectrum as a function of energy, which is precisely what the oscillation model predicts. The real clincher, however, is that the suppression is much less than that seen for solar neutrinos because their oscillation is modified as they pass through the dense matter of the Sun. This is exactly what is expected for a model of neutrino oscillations, but not for any of the other models, and seems to be the final piece of evidence needed to state that neutrinos really do oscillate. Furthermore, it allows us to measure Δm122 accurately, which, combined with the solar-neutrino measurements, constrains the values of the neutrino-oscillation parameters.
Long-baseline experiments
If terrestrial experiments like KamLAND can observe the neutrino oscillations originally seen by solar-neutrino experiments, are there terrestrial experiments that can detect the oscillations seen in atmospheric neutrinos? The answer is yes, but it means we have to make our own high-energy neutrinos, and this requires an accelerator.
The idea of creating a pure, collimated beam of neutrinos has been around since the muon neutrino was discovered in the early 1960s. The starting point is to send a beam of protons into some target to produce pions, which then decay to produce a beam of muons and muon neutrinos. By stopping the muons before all but a very few can decay, a beam consisting almost solely of muon neutrinos emerges. Two types of experiments can be done with such a beam. First, one can look for a reduction in the flux of muon neutrinos from the expected value as a function of energy or distance; and second, one can look for electron or tau neutrinos in the beam that could not have been there when it was generated.
Experiments of this latter type have a long history, but we now know they were looking in the wrong place. Guided by a theoretical prejudice that all the mixing angles would be small and by the belief that neutrino masses should be large enough to explain the missing matter in the universe, researchers were looking for small mixing angles and large mass differences. But we now know from the results of solar, atmospheric and reactor oscillation experiments that we should be looking for small mass differences and large mixing angles, and a new generation of experiments has been designed to do just that.
The first of these, called K2K, produced its first results in 2000. The proton beam is produced at the KEK laboratory just north of Tokyo, and the resulting muon-neutrino beam is fired 250 km under Japan to the SuperKamiokande detector. Sure enough, this experiment has seen too few muon neutrinos, exactly as would be expected if the atmospheric-neutrino anomaly really is caused by neutrino oscillations.
A number of other such long-baseline experiments are either under construction or being planned. The first of these, called MINOS, will fire an intense beam of muon neutrinos from Fermilab near Chicago to a detector in the Soudan mine in Minnesota (a distance of 735 km). Unlike water Cerenkov detectors, MINOS consists of a large iron calorimeter in the presence of a magnetic field, which can track and measure the momentum of charged particles as they pass through the detector. MINOS can therefore make a more precise measurement of the energy spectrum of the muons arising from interactions with the Fermilab neutrinos, and thus allow a more precise determination of the energy at which the oscillations are at a maximum. This will allow us make better measurements of Δm232, which is currently poorly determined.
Another long-baseline experiment called CNGS is under construction in Europe, where muon neutrinos will be fired from CERN in Geneva to the Gran Sasso National Laboratory near Rome (a distance of 730 km). The two large detectors being built at Gran Sasso – OPERA and ICARUS – will make extremely precise measurements of the resulting particle tracks. By actually observing tau neutrinos in the beam, this should enable the CNGS team to confirm a central prediction of our current models of neutrino oscillations – that the atmospheric-neutrino anomaly is caused primarily by the oscillation of muon to tau neutrinos.
I believe it was Eddington who said that anything that is consistent with all existing experimental data must be wrong, because some of the data are almost certainly wrong. For those who wish to believe in neutrino oscillations it is therefore a relief that one experiment – LSND at Los Alamos – does not fit into the neutrino picture outlined here.
In 1996 the LSND team claimed to see evidence for the appearance of electron neutrinos in a muon-neutrino beam, which suggested a small mixing angle and a relatively large value of Δm122. Although another experiment with similar sensitivity called KARMEN at the Rutherford Appleton Laboratory in the UK has seen no evidence for this effect, the results of a dedicated experiment called MiniBooNE are keenly awaited. The MiniBooNE detector is based at Fermilab, and will search for electrons in a beam of muon neutrinos produced by Fermilab’s proton accelerator. If MiniBooNE sees no effect, then everyone, except possibly Eddington, can breathe a sign of relief and believe the three-neutrino oscillation picture painted by the existing experiments. On the other hand, if MiniBooNE confirms the LSND result then we live in a very strange world indeed and the mixing phenomenon would have to be much more complex than our current understanding.
Measuring θ13: the next step in the story
So where do we stand with the measurements of the fundamental neutrino-oscillation parameters? Solar-neutrino experiments and KamLAND have measured the angle θ12 to be about 32° and the mass difference Δm122 to be about 8 x 10-5 eV2. Atmospheric-neutrino oscillation measurements have constrained θ23 to be nearly 45° (i.e. neutrinos oscillate as much as is possible) and also measured Δm232 to be about 2.5 x 10-3 eV2. This leaves the third mixing angle, θ13.
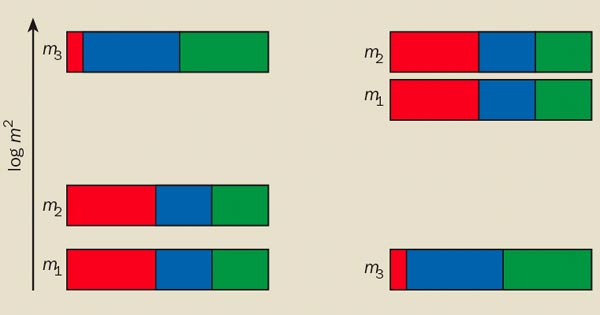
We also need to know a bit more about the neutrino-mass states. With three different masses there are only two independent mass differences, and since we have already measured two mass differences you might think we were done. Unfortunately, it is not that simple. The reason why is that we do not know a priori the ordering of the mass states, because the vacuum-neutrino oscillations we have measured depend on the square of the mass differences and are therefore independent of their sign. But matter effects, such as those present for neutrinos that escape the dense interior of the Sun, do depend on the sign of the mass difference. We therefore know from the oscillations of solar neutrinos that ν2 is more massive than ν1. But since we have not yet seen any matter effects in the oscillations of atmospheric neutrinos, because the Earth is not sufficiently dense, there are two remaining possible orderings (figure 2).
Determining θ13 and the mass hierarchy is the target of the next generation of planned experiments. We already know from experiments on shorter baselines than KamLAND that the angle θ13, unlike the other two angles, is small. New experiments plan to look for θ13 in the so-called sub-leading oscillations that arise when the effects of all three neutrinos are taken into account. These oscillations would produce small ripples on the primary oscillation pattern, and cause the additional appearance of electron neutrinos in a terrestrial muon-neutrino beam. New reactor and accelerator oscillation experiments have been proposed that will use a near detector and a far detector in order to improve the sensitivity to tiny suppressions and small appearance probabilities, and hence to smaller values of θ13.
Long-baseline experiments such as MINOS offer some sensitivity to these second-order effects, but to significantly improve on our existing knowledge we will require entirely new facilities using even more intense neutrino beams. The first of these “superbeam” experiments, called T2K, is currently being built in Japan, and will involve firing a neutrino beam with unprecedented intensity through 295 km of rock from the JPARC facility on the east coast of the country to SuperKamiokande on the west. At the energies and distances involved, the type of oscillations seen in solar neutrinos will not produce any significant effect, so any electron neutrinos seen in the muon-neutrino beam would be a signal of oscillations modulated by the third angle θ13.
Another new experiment called NOvA is planned at Fermilab, which will utilize the same beam used for MINOS. This experiment will be at higher energies and longer baselines than the T2K experiment, which will hopefully allow matter effects to be observed and enable us to determine the mass hierarchy.
The more distant future: the neutrino factory
So what does all this have to do with the excess of matter over antimatter in the universe, as promised all those words ago? A clue could lie in the parameter δ. Producing a matter-antimatter asymmetry requires the laws of physics to be different for matter and antimatter, and a non-zero value of δ would indeed lead to differences in the oscillations of neutrinos and antineutrinos. A related effect in the early universe called leptogenesis could then lead to a matter-antimatter imbalance. But leptogenesis depends on parameters that cannot be measured on Earth, so we must therefore first measure δ and then trust our theorists to find the right model to connect δ to leptogenesis.
The basic idea is simple: you start with a beam of muon neutrinos and measure the probability that they change into electron neutrinos, then switch to a beam of muon antineutrinos and measure the probability of a transition to electron antineutrinos at the same energy and baseline. Any difference would indicate that δ is not zero, provided that you pass the antineutrinos through an antimatter Earth and allow them to interact with an antimatter detector. Unfortunately this is beyond the science budgets of most countries, so we have to measure both neutrinos and antineutrinos with a detector made of ordinary matter and correct for the uninteresting differences that this introduces (which limits the sensitivity of the experiment).
Superbeam neutrino experiments may be sensitive to values of δ that are near π/2 or 3π/2, where CP violation is the largest (see box 2 below), but to really pin this angle down we need even more intense and “cleaner” neutrino beams. A feasibility study is currently taking place at CERN to find out if this can be achieved with beams of unstable nuclei, which undergo beta decay and produce pure beams of electron neutrinos or antineutrinos.
An even more ambitious plan is to build a “neutrino factory”, which would produce very pure and intense neutrino beams that could be fired thousands of kilometres through the Earth to distant detectors. Such a machine would make pions, which would decay into muons, as in a conventional long-baseline experiment. But it would then accelerate these muons to high energies so that they produce a collimated neutrino beam with a well-known energy when they decay. This would allow us to measure neutrino oscillations with a sensitivity that is orders of magnitude better than any other planned experiment, although the difficulty and expense of such an undertaking are considerable.
One major challenge is to find a way to collect and accelerate the muons before they have time to decay. Existing methods to “cool” particles by reducing their angular or energy spread are too slow to be used for muons (which rapidly decay into other particles). This has led to a major international experiment called MICE (Muon Ionization Cooling Experiment) at the Rutherford Appleton Laboratory that will test an entirely new type of cooling (see Physics World April p5). Technological developments such as MICE should make it possible to build a neutrino factory some time soon, hopefully before I retire in about 20 years.
The pay-off
So, neutrino oscillations have been discovered. But it is worth remembering that both confirmed observations of neutrino oscillations arose from experiments that were initially built to look for something else. In fact, when Ray Davis originally proposed his experiment, most people thought it was a waste of time (one reviewer even compared it to trying to measure the distance to the Moon by standing on a ladder and holding up your hand!). In today’s hypercompetitive funding system, it is very doubtful that Davis could have secured the resources to build the experiment at all. We must therefore be careful that we do not squeeze out the sense of adventure and curiosity that leads to the entirely new. Not finding exactly what you were looking for is not a risk to be mitigated in designing experiments, it is why we do experiments.
Neutrino oscillations may seem an odd quirk of quantum mechanics, but they could help us understand particle physics at a far deeper level. Paradoxically, the very smallness of neutrino masses leads many theorists to believe that they provide a window on physics at much higher energies than our accelerators can reach. The mixing of neutrinos, which can, in principle, be measured even more accurately than the more familiar mixing of quarks, may help explain the puzzle of why there are three versions of all the particles in the first place. Neutrino mass is important in our understanding of the universe as a whole, and, furthermore, neutrinos may have generated all the matter from which we are made. Not a bad pay-off for a tank of cleaning fluid and some wonky backgrounds in a proton-decay experiment.
Box 1: Neutrino oscillations in theory
If neutrinos have mass, then the identity of a given neutrino becomes a bit complicated. This is because in addition to the electron (νe), muon (νμ) and tau (ντ) “flavour” states that have well-defined weak interactions, neutrinos have another set of states – denoted ν1, ν2 and ν3 – that have well-defined masses. Any particular neutrino will appear either as a νe, νμ or ντ if a measurement is sensitive to weak interactions, or as a ν1, ν2 or ν3 if a measurement is sensitive to mass. It is possible for these two sets to be the same, but, in general, they will be “mixed”. In other words, a νe will be partly ν1, partly ν2 and partly ν3, and similarly for νμ and ντ.
If we consider mixing between just two neutrino states as an example, this mixing can be described in terms of a single mixing angle θ (see equation 1).
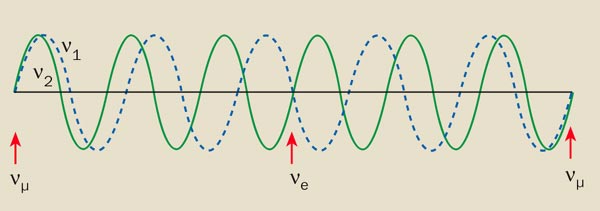
Real-life reactions produce flavour states: for instance, thermonuclear reactions in the Sun generate only νe. However, it is the mass states that propagate through space. If we take the simplest case of θ = 45°, the above equation states that νe = ν1 – ν2 and νμ = ν1 + ν2. Recalling that particles can also be described as waves, this means that the ν1 and ν2 waves are oscillating out of phase in the case of a νe, while ν1 and ν2 are in phase for νμ. If ν1 and ν2 have different masses, they will also have different wavelengths, and thus their relative phases will change with time or distance (see wavelength diagram).
If we start with a pure νμ beam (left), the ν1 and ν2 waves will eventually become completely out of phase and appear as a ne (middle), before changing back into a νμ as the beam continues to propagate (right). The speed with which this change of identity takes place depends on the difference between the two wavelengths, which depends on the differences between the squares of the masses of ν1 and ν2, Δm122 = m22 – m12. In fact, the probability of finding a νμ in an initially pure nm beam with an energy E after it has travelled a distance L is given by (see equation 2).
When the neutrinos are travelling through empty space, the decrease in the overall νμ flux (and the corresponding increase in the νe flux) thus depends on the amount of mixing, θ. However, since a νe experiences slightly different interactions in matter compared with a νμ or a ντ, the oscillations can actually be enhanced when a neutrino passes through the Sun or the Earth. Real experiments also involve all three neutrinos, which can lead to “oscillations on oscillations” that will be significant in future experiments (see text). Three-flavour oscillations require more parameters to be measured than in the two-flavour case described here: three mixing angles (θ12, θ23 and θ13), two independent mass differences (Δm122 and Δm232) and one additional parameter, δ, which could produce differences in the oscillations of neutrinos and antineutrinos.
Box 2: Neutrinos and CP violation
In 1967 the Russian physicist Andre Sakharov showed that in order to get from an initial state dominated by energy to the matter-dominated universe we see today, three conditions have to be met. First, the laws of physics must produce matter and antimatter in different amounts; second, the number of baryons, such as neutrons and protons, must not be conserved; and third, the universe cannot be in thermal equilibrium. The latter two conditions seem easy enough to satisfy, but the first condition – which is also known as charge-parity (CP) violation – has proved more problematic.
CP violation had, in fact, already been observed in 1964 in the decays of neutral kaons and their antiparticles, and a mechanism to explain it was introduced into the Standard Model. More recently, observations of the decays of neutral B-mesons have confirmed that this simple and elegant explanation works more generally, which is a triumph for theoretical physics. But the amount of CP violation produced by the Standard Model is too small by many orders of magnitude to explain the observed excess of matter in the universe, forcing us to conclude that there must be some additional process that violates CP.
Neutrino physics offers one of the more attractive possibilities for this, and raises the prospect that neutrinos might be the first known example of what is called a Majorana particle – a matter particle that is its own antiparticle. One consequence of this might be a process known as leptogenesis, by which CP violation in the decays of very heavy neutrinos in the early universe could create an excess of matter over antimatter. This could, in turn, be related to the CP-violating phase, δ, that is potentially observable in neutrino-oscillation experiments.
Further reading
Q R Ahmad et al. (SNO Collaboration) 2002 Direct evidence for neutrino flavor transformation from neutral-current interactions in the Sudbury Neutrino Observatory Phys. Rev. Lett. 89 011301
S N Ahmed et al. (SNO Collaboration) 2004 Measurement of the total active 8B solar-neutrino flux at the Sudbury Neutrino Observatory with enhanced neutral-current sensitivity Phys. Rev. Lett. 92 181301
E Aliu et al. (K2K Collaboration) 2005 Evidence for muon-neutrino oscillation in an accelerator-based experiment Phys. Rev. Lett. 94 081802
T Araki et al. (KamLAND Collaboration) 2005 Measurement of neutrino oscillation with KamLAND: evidence of spectral distortion Phys. Rev. Lett. 94 081801
Y Ashie et al. (SuperKamiokande Collaboration) 2004 Evidence for an oscillatory signature in atmospheric-neutrino oscillations Phys. Rev. Lett. 93 101801
G Drexlin 2003 Final neutrino oscillation results from LSND and KARMEN Nucl. Phys. B (Proc. Suppl.) 118 146–153
Y Fukuda et al. (SuperKamiokande Collaboration) 1998 Evidence for oscillation of atmospheric neutrinos Phys. Rev. Lett. 81 1562
H Murayama 2002 The origin of neutrino mass Physics World May pp35–39 (print edition only)