Entanglement is a fundamental concept in quantum information theory and is often regarded as a key indicator of a system’s “quantumness”. However, the relationship between entanglement and quantum computational power is not straightforward. In a study posted on the arXiv preprint server, physicists in Germany, Italy and the US shed light on this complex relationship by exploring the role of a property known as “magic” in entanglement theory. The study’s results have broad implications for various fields, including quantum error correction, many-body physics and quantum chaos.
Traditionally, the more entangled your quantum bits (qubits) are, the more you can do with your quantum computer. However, this belief – that higher entanglement in a quantum state is associated with greater computational advantage – is challenged by the fact that certain highly entangled states can be efficiently simulated on classical computers and do not offer the same computational power as other quantum states. These states are often generated by classically simulable circuits known as Clifford circuits.
To address this discrepancy, researchers introduced the concept of “magic”. Magic quantifies the non-Clifford resources necessary to prepare a quantum state and thus serves as a more nuanced measure of a state’s quantum computational power.
Studying entanglement and magic
In the new study, Andi Gu, a PhD student at Harvard University, together with postdoctoral researchers Salvatore F E Oliviero of Scuola Normale Superiore and CNR in Pisa and Lorenzo Leone of the Dahlem Center for Complex Quantum Systems in Berlin, approach the study of entanglement and magic by examining operational tasks such as entanglement estimation, distillation and dilution.
The first of these tasks quantifies the degree of entanglement in a quantum system. The goal of entanglement distillation, meanwhile, is to use LOCC (local operations and classical communication) to transform a quantum state into as many Bell pairs as possible. Entanglement dilution, as its name suggests, is the converse of this: it aims to convert copies of the Bell state into less entangled states using LOCC with high fidelity.
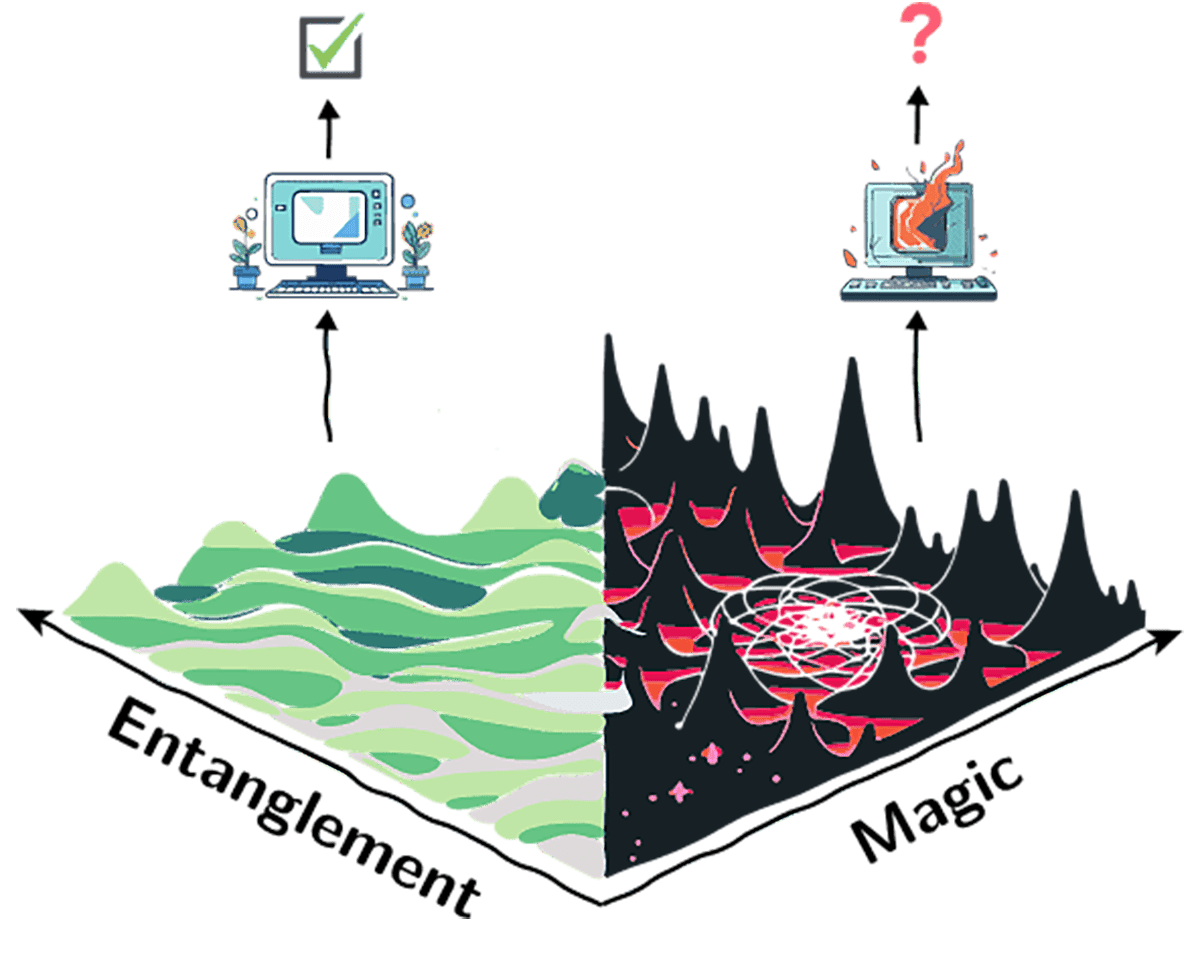
Gu and colleagues find a computational phase separation between quantum states, dividing them into two distinct regimes: the entanglement-dominated (ED) and magic-dominated (MD) phases. In the former, entanglement significantly surpasses magic, and quantum states allow for efficient quantum algorithms to perform various entanglement-related tasks. For instance, entanglement entropy can be estimated with negligible error, and efficient protocols exist for entanglement manipulation (that is, distillation and dilution). The research team also propose efficient ways to detect entanglement in noisy ED states, showing their surprising resilience compared to traditional states.
In contrast, states in the MD phase have a higher degree of magic relative to entanglement. This makes entanglement-related tasks computationally intractable, highlighting the significant computational overhead introduced by magic and requiring more advanced approaches. “We can always handle entanglement tasks efficiently for ED states, but for MD states, it’s a mixed bag – while there could be something that works, sometimes nothing works at all,” Guo, Leone and Oliviero tell Physics World.
Practical implications
As for the significance of this separation, the trio say that in quantum error correction, understanding the interplay between entanglement and magic can improve the design of error-correcting codes that protect quantum information from decoherence (a loss of quantumness) and other errors. For instance, topological error-correcting codes that rely on the robustness of entanglement, such as those in three-dimensional topological models, benefit from the insights provided by the ED-MD phase distinction.
The team’s proposed framework also offers theoretical explanations for numerical observations in hybrid quantum circuits (random circuits interspersed with measurements), where transitions between phases are observed. These findings improve our understanding of the dynamics of entanglement in many-body systems and demonstrate that entanglement of states within the ED phase is robust under noise.

Quantum error correction produces better ‘magic’ states
The trio say that next steps for this research could take several directions. “First, we aim to explore whether ED states, characterized by efficient entanglement manipulation even with many non-Clifford gates, can be efficiently classically simulated, or if other quantum tasks can be performed efficiently for these states,” they say. Another avenue would be to extend the framework to continuous variable systems, such as bosons and fermions.



