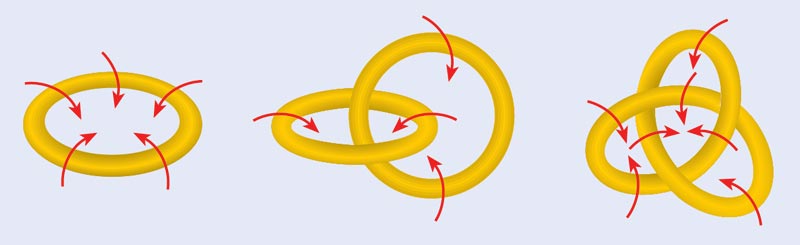
In 1867 Lord Kelvin (then known as William Thomson) witnessed a demonstration of a machine that could produce smoke rings. Built by his friend and fellow physicist Peter Tait, the machine was much more than an interesting novelty. At the time, smoke rings were a hot topic in physics, thanks to work by Hermann von Helmholtz and, later, Kelvin himself. Helmholtz had shown that in a perfectly dissipationless fluid, the “lines of vorticity” around which fluid flows are conserved quantities. Hence, in such a fluid the vortex loop configurations, such as smoke rings, should persist for all time. Since scientists believed that the entire universe was filled with just such a perfect dissipationless fluid, known as the “luminiferous aether”, Kelvin suggested that different knotting configurations of vortex lines in the aether might correspond to different atoms (figure 1).

This theory of “vortex atoms” was appealing because it gave a reason for why atoms are discrete and immutable. For several years the theory was quite popular, attracting the interest of other great scientists such as Maxwell. However, after further research and failed attempts to extract predictions from it, the idea lost popularity. The theory of the vortex atom was finally killed altogether when Michelson and Morley (and later Einstein) showed that the aether does not exist.

Nonetheless, some of the theory’s proponents remained enthusiastic about it for quite some time, and perhaps its greatest supporter was Tait himself. Although initially quite sceptical, Tait eventually came to believe that by building a table of all possible knots, he would gain some insight into the periodic table of the elements. In a groundbreaking series of papers, he constructed a catalogue of all knots with up to seven crossings. (Note that mathematicians make a distinction between “knots” made from a single strand and “links” made of multiple strands. We will be sloppy and call them all knots.) Although the vortex-atom theory came to nothing, these studies made Tait the father of the mathematical theory of knots – which has since been a rich field of study in mathematics.

More recently, a remarkable connection between knot theory and certain quantum systems has emerged. This connection is now being explored both theoretically and experimentally, in part because of the promise it holds for quantum information processing. It turns out that although we cannot make atoms out of knotted strands of aether, it may be possible to make a quantum computer by dragging particles around each other to form particular types of space–time knots. And while such a “topological quantum computer” would be difficult to construct, it would offer some advantages over more conventional schemes for quantum information processing.

An invariably knotty problem

To understand how a topological quantum computer might work, we must first explore a mathematical concept called a “knot invariant”. During his attempt to build a “periodic table of knots”, Tait posed what has become perhaps the fundamental question in mathematical knot theory: how do you know if two knots are topologically equivalent or topologically different? In other words, can two knots be smoothly deformed into each other without cutting any of their strands? Although this is still considered to be a difficult mathematical problem, the knot invariant is a powerful tool that can help in solving it.

A knot invariant is defined as a mathematical algorithm that connects a picture of a knot – the input – to some output via a set of rules. The rules are chosen such that if two knots that are input are topologically equivalent, then applying the rules will always give the same output. Hence, if two outputs are different, one knows immediately that the two input knots were not topologically equivalent.

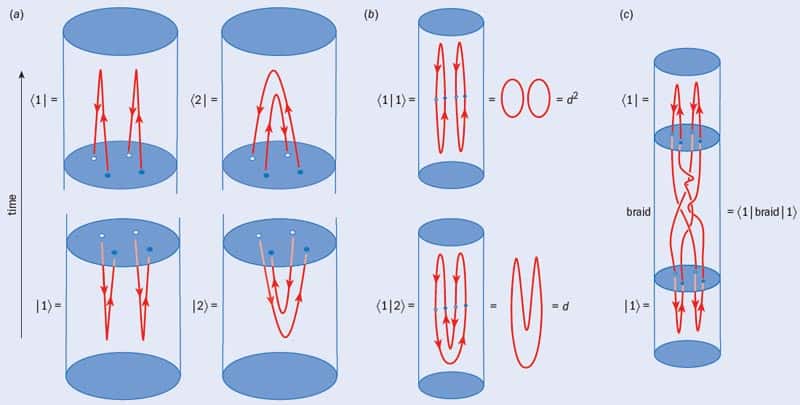
One of the simplest types of knot invariant is known as the Kauffman invariant, and it is defined by just two rules (figure 2a). Whenever we see two strands cross in our picture of a knot, we can use the first rule to replace our picture with a “sum” of two pictures, each with one fewer crossing than the original picture, and with a parameter A that acts as a kind of bookkeeping tool to keep track of how many right- versus left-handed crossings we have replaced. By repeatedly using this first rule, we can eventually reduce our picture to a sum of diagrams that have no crossings at all – they are just open loops. We then use the second rule to replace each open loop with the value d = –A² –A^–2, yielding a polynomial in A and A^–1. An example of evaluating the Kauffman invariant is shown in figure 2b, where we find (after using some algebra) that the Kauffman invariant of the double figure-of-eight picture we started with is in fact the same as that of the open loop – which is what we should expect, given that they are topologically equivalent.

Figure 2c shows a slightly more complicated example, which reveals that the Kauffman invariant of a piece of twisted string is not the same as the invariant of the untwisted string – in fact, their invariants differ by a factor of –A³. This may seem to contradict the description above that the Kauffman invariant should be the same for any two knots that can be smoothly deformed into each other (since it appears we can smoothly deform the twisted string into the straight one). However, we should think of the strands not as being infinitely thin, but rather as having some width (figure 2d). In this case, it is easy to see that if we try to smoothly remove the twist by pulling the string straight, then we actually still end up with a twist in our strand.

Different paths, same outcome

To understand the connection between knot invariants and physics, we need to think about quantum mechanics in the manner pioneered by Richard Feynman in his path-integral approach to calculating the probability of a particular quantum event. Using Feynman’s method, the probability of getting from an initial to a final configuration can be calculated by summing up the probability amplitudes of all possible processes (or “paths”) that can happen between the initial and final states.

For some very special types of quantum systems, the amplitude of a particular process will depend only on the topology of that process, not on any precise details of the process such as how fast particles move or how far apart they are. Roughly speaking, this means that particles in the system can move around each other in many different ways – they can even be created out of the vacuum as particle–hole or particle–antiparticle pairs – but if the paths they trace out in space–time are topologically equivalent, then those paths will be equally probable. Systems that obey this rule are known as topological quantum systems, and the theories describing their behaviour are called topological quantum field theories (TQFTs).

This brings us to a rather remarkable conclusion: in a topological quantum system, the amplitude for a particular process is a knot invariant of the space–time paths traced out by the particles during that process. Do not worry if this connection seems less than obvious. The mathematical physicist Ed Witten, who was the first to make it, won the highest honour in mathematics – the Fields Medal – for his achievement. The essence of his insight is that a knot invariant is defined as an output that depends only on the topology of the knot input, and the amplitudes in a TQFT also depend only on the topology of the knot formed by the particles’ paths through space–time. So, the amplitudes must be knot invariants.

Before we proceed, it is worth emphasizing that when we talk about particle paths, we are actually considering world-lines – paths in both space and time. For example, if we have a 2D (flat) physical system, we must view time as the third dimension. Hence, a particle at rest will trace out a straight space–time world-line in two spatial dimensions and one time dimension, while two particles orbiting around each other in two dimensions will form a double helix or two-stranded braid in (2 + 1) dimensions. All the TQFTs that we will be interested in are indeed 2D (flat) systems where we can think of the third dimension as time.

To see an example of how the correspondence between amplitudes and knot invariants works in practice, let us return for a moment to figure 2d. In the language of the TQFT, we see that a particle that rotates around itself, creating a twisted path in space–time, accumulates a factor of –A³ compared with a particle that does not rotate around itself. This additional factor obtained by evaluating the Kauffman invariant is actually something we should expect if we think about amplitudes for world-lines of particles in a quantum-mechanical system. We know that when a particle rotates in quantum mechanics, it will generally pick up a phase due to its spin – and indeed in all physically realizable TQFTs, –A³ is just such a phase.

Multiparticle systems

Perhaps the most important property of these TQFTs occurs when there are multiple particles and holes created. In topological quantum systems composed of multiple particles, there are generally many different (orthogonal) wavefunctions with the same energy describing the state of the system. This is quite unusual since, for most quantum systems, once all locally measurable quantum numbers (position, spin and so on) are specified, then the wavefunction is uniquely defined. But for TQFTs there are additional hidden “topological” degrees of freedom – so there can be several wavefunctions that have exactly the same energy, and look exactly the same to all local measurements, but still represent different quantum states.

To see how this occurs, consider a system containing two identical particles and two identical holes (figure 3a). The crucial thing to realize is that this system can be prepared with (at least) two topologically distinct space–time histories. We will call these two (ket) states |1〉 and |2〉. Their corresponding (bra) states 〈1| and 〈2| are the same as |1〉 and |2〉 but with time reversed.

The next question we need to resolve is whether |1〉 and |2〉 are in fact different quantum states. To demonstrate that they are, we need to calculate their overlap amplitudes, such as 〈1|1〉 and 〈1|2〉, and check that these are different. In other words, we need to show that |1〉 and |2〉 are linearly independent (figure 3b). The procedure for doing this is quite obvious: we simply bring together the two corresponding space–time pictures to form a closed knot and then evaluate the Kauffman invariant of the result. Bringing together 〈1| with |1〉, or 〈2| with |2〉, generates two loops, resulting in a Kauffman invariant of d² (in other words, 〈1|1〉 =  〈2|2〉 = d²). However, bringing together 〈1| with |2〉 generates only one loop, giving 〈1|2〉 = d. This immediately tells us that |1〉 and |2〉 must be different quantum states as long as |d| ≠ 1. It is also possible to show that any other, more complicated, way of preparing the configuration of two particles and two holes must be some linear combination of |1〉 and |2〉. We therefore conclude that our two-particle, two-hole system is precisely a two-state quantum system, or a single quantum bit (qubit).

We can use the same technique to calculate, for example, 〈1|braid|1〉 by evaluating the Kauffman invariant of a braided knot (figure 3c). In this case we conclude that the process of braiding particles around each other in space–time generally performs (unitary) transformations on our two-state quantum systems. In other words, we are manipulating the quantum state of our qubit by braiding particles around each other.

A quantum computer in theory…

Being able to use particle paths to perform mathematical operations raises the interesting possibility of using topological quantum systems as a quantum computer. This idea, known as “topological quantum computation”, is generally credited to Michael Freedman (another Fields medallist) and Alexei Kitaev. One implementation of the general scheme is illustrated in figure 4. In this three-qubit scheme, quartets of particles are pulled from the vacuum, with each four particles representing a single qubit of information. In the parlance of quantum computation, this is called the “initialization” phase. A quantum computation is achieved by dragging the particles around each other to form a particular knot, with different types of braids corresponding to different quantum computations. Finally, one makes a measurement at the end by, say, attempting to annihilate the pairs of particles. Those particles that do not annihilate (because their amplitude for annihilation is zero as calculated by the Kauffman invariant) make up the “readout” of the computation. Of course, one could predict the outcome of this experiment by calculating the Kauffman invariant of the knot using the rules laid out in figure 2a. However, it is quite clear that applying these recursive rules becomes impossibly complicated for all but the simplest knots, whereas a physical topological quantum system can automatically perform this calculation for very complicated knots with no trouble.

While this topological quantum computation may sound like an extremely complicated way to achieve the already difficult goal of building a quantum computer, if one starts with the right topological quantum system, then it turns out to be just as capable of performing standard quantum-computational tasks (such as Shor’s algorithm for finding prime factors of large integers) as any other approach to building a quantum computer, at least in principle. Indeed, it actually has one very important advantage – again, in principle – over other schemes that have been proposed.

The advantage of a topological quantum computer stems from the fact that one of the main difficulties with building a quantum computer is finding a way to protect it from small errors, and particularly to protect it from noise and other factors that couple to the environment. In a topological computer, if noise hits the device in the middle of a computation, a particle may be shaken around a bit (figure 4). However, as long as the overall topology of the braid is unchanged, then the computation being performed is also unchanged and no error occurs. In this way, a topological quantum computer is naturally protected from errors – a rather substantial advantage.

…and in practice?

This advantage would, however, be pointless if there were no real, physical systems that obey the rules of TQFTs. But while quantum systems that are described by knot invariants in this way may sound rather exotic, in fact a few such systems are believed to exist. One class of systems are 2D p-wave superfluids, including Sr₂RuO₄ superconducting films, helium-3A superfluid films and the so-called ν = 5/2 and ν = 7/2 quantum Hall systems. Closely related are various (yet to be realized) proposals for creating superconducting structures on the surface of topological insulators and other systems with strong spin–orbit coupling. The experimentally observed ν = 12/5 quantum Hall system is another example thought to be a particularly interesting class of topological quantum system. Finally, there have been many proposals to realize such systems in ultra-cold atomic lattices or in ultra-cold rotating bosons.

Although TQFTs may end up being applicable for any one of a number of physical systems, the strongest candidates for a real-life topological quantum system are the above-mentioned ν = 5/2 and 7/2 quantum Hall states. Quantum Hall states can form when electrons are confined to two dimensions, exposed to large magnetic fields and cooled to very low temperatures. Under such conditions, the ratio of the density of electrons to the applied magnetic field, ν, takes certain simple values such as 1, 2, 1/3, 2/5 and so forth. When the ratio is a fraction, the effect is known as the fractional quantum Hall effect. Electrons in quantum Hall states (fractional or otherwise) can flow with no dissipation – a situation analogous to the flow in superfluids and superconductors. Crucially, when these quantum Hall states form, the individual electrons form a uniform-density quantum fluid and one need only keep track of the low-energy “quasiparticles” – quantized lumps of charge density in an otherwise uniform fluid. Since all charges have a tendency to move in orbits in a magnetic field, the quasiparticles can be thought of as vortices in a perfectly dissipationless fluid – which, just as Kelvin predicted, are stable configurations of fluid flow – and it is these quasiparticles that are expected to obey the braiding physics of a TQFT.

One reason to be optimistic about these systems is that they have an amazing property: electrical measurements made on them do not depend on certain details of the experiment. In particular, their longitudinal resistance is always zero, while their Hall resistance (figure 5) is always independent of the shape of the sample and how the electrical contacts are positioned. This independence of detailed geometry is a strong hint that these systems are described by a TQFT. Some preliminary (albeit currently controversial) experimental evidence that these states of matter really are non-trivial TQFTs has been recently reported by Robert Willett and colleagues (arXiv:0911.0345). If their work is convincingly verified, then it would provide proof that the physics of knot theory is being realized in quantum systems. This would be an amazing development from the perspective of fundamental physics – but it would also open the door to applying the physics of knots to building a topological quantum computer.

At a glance: Topological quantum computing

• The first major mathematical studies of knots began after 19th-century physicists suggested that atoms could be made from knotted strands of vortices in the “luminiferous aether”
• Knot invariants can help determine whether two knots are “topologically equivalent”, meaning they can be deformed into each other smoothly and without cutting any strands
• In some very special quantum systems, the probability that a particular process will occur depends entirely on the system’s topology. In such cases, the probability amplitude is equivalent to the knot invariant of the space–time paths traced out by particles during the process
• It is possible to manipulate the quantum state of such systems by dragging particles around each other to create certain types of knotted patterns in space–time
• Computations performed in this way would be less vulnerable to noise than other types of quantum computers because the result of a computation depends only on the topology of the knot, not the paths of the particles that formed it

More about: Topological quantum computing

N E Bonesteel et al. 2005 Braid topologies for quantum computation Phys. Rev. Lett. 95 140503
M H Freedman, M J Larsen and Z Wang 2002 A modular functor which is universal for quantum computation Commun. Math. Phys. 227 605
L H Kauffman 2001 Knots and Physics 3rd edn (New York, World Scientific)
A Kitaev 2003 Fault-tolerant quantum computation by anyons Ann. Phys., NY 303 2
A Kitaev 2006 Anyons in an exactly solved model and beyond Ann. Phys., NY 321 2
C Nayak et al. 2008 Non-Abelian anyons and topological quantum computation Rev. Mod. Phys. 80 1083