
Researchers at Google Quantum AI and collaborators have developed a quantum processor with error rates that get progressively smaller as the number of quantum bits (qubits) grows larger. This achievement is a milestone for quantum error correction, as it could, in principle, lead to an unlimited increase in qubit quality, and ultimately to an unlimited increase in the length and complexity of the algorithms that quantum computers can run.
Noise is an inherent feature of all physical systems, including computers. The bits in classical computers are protected from this noise by redundancy: some of the data is held in more than one place, so if an error occurs, it is easily identified and remedied. However, the no-cloning theorem of quantum mechanics dictates that once a quantum state is measured – a first step towards copying it – it is destroyed. “For a little bit, people were surprised that quantum error correction could exist at all,” observes Michael Newman, a staff research scientist at Google Quantum AI.
Beginning in the mid-1990s, however, information theorists showed that this barrier is not insurmountable, and several codes for correcting qubit errors were developed. The principle underlying all of them is that multiple physical qubits (such as individual atomic energy levels or states in superconducting circuits) can be networked to create a single logical qubit that collectively holds the quantum information. It is then possible to use “measure” qubits to determine whether an error occurred on one of the “data” qubits without affecting the state of the latter.
“In quantum error correction, we basically track the state,” Newman explains. “We say ‘Okay, what errors are happening?’ We figure that out on the fly, and then when we do a measurement of the logical information – which gives us our answer – we can reinterpret our measurement according to our understanding of what errors have happened.”
Keeping error rates low
In principle, this procedure makes it possible for infinitely stable qubits to perform indefinitely long calculations – but only if error rates remain low enough. The problem is that each additional physical qubit introduces a fresh source of error. Increasing the number of physical qubits in each logical qubit is therefore a double-edged sword, and the logical qubit’s continued stability depends on several factors. These include the ability of the quantum processor’s (classical) software to detect and interpret errors; the specific error-correction code used; and, importantly, the fidelity of the physical qubits themselves.
In 2023, Newman and colleagues at Google Quantum AI showed that an error-correction code called the surface code (which Newman describes as having “one of the highest error-suppression factors of any quantum code”) made it just about possible to “win” at error correction by adding more physical qubits to the system. Specifically, they showed that a distance-5 array logical qubit made from 49 superconducting transmon qubits had a slightly lower error rate than a distance-3 array qubit made from 17 such qubits. But the margin was slim. “We knew that…this wouldn’t persist,” Newman says.
“Convincing, exponential error suppression”
In the latest work, which is published in Nature, a Google Quantum AI team led by Hartmut Neven unveil a new superconducting processor called Willow with several improvements over the previous Sycamore chip. These include gates (the building blocks of logical operations) that retain their “quantumness” five times longer and a Google Deepmind-developed machine learning algorithm that interprets errors in real time. When the team used this new tech to create nine surface code distance-3 arrays, four distance-5 arrays and one 101-qubit distance-7 array on their 105-qubit processor, the error rate was suppressed by a factor of 2.4 as additional qubits were added.
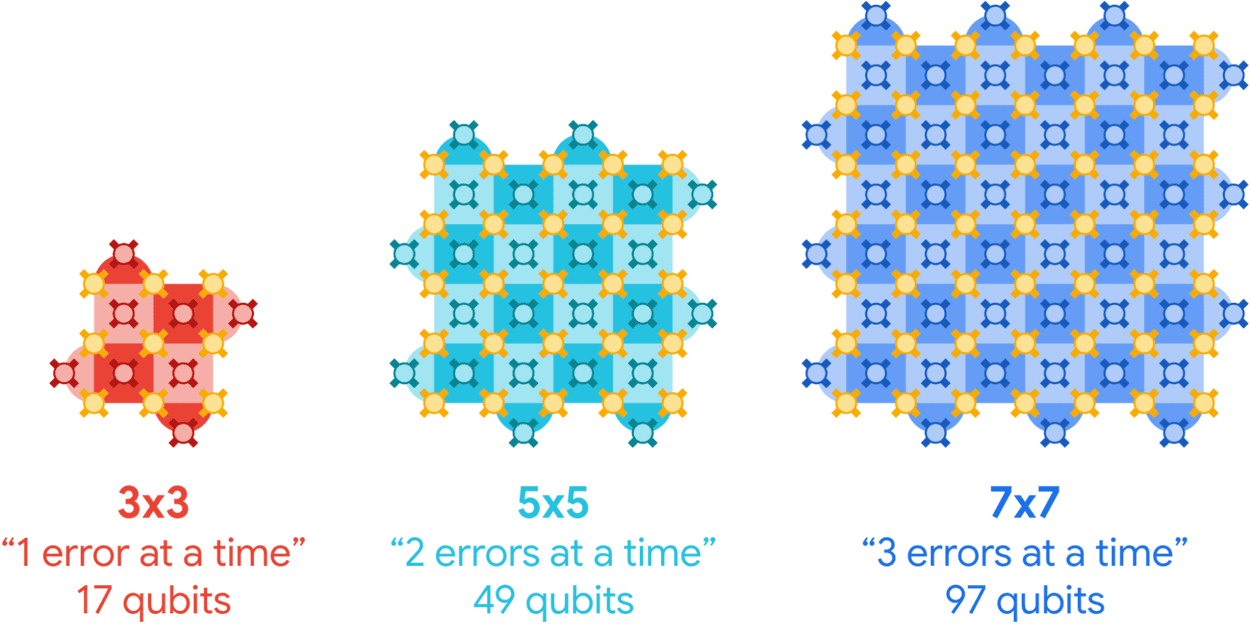
“This is the first time we have seen convincing, exponential error suppression in the logical qubits as we increase the number of physical qubits,” says Newman. “That’s something people have been trying to do for about 30 years.”
With gates that remain stable for hours on end, quantum computers should be able to run the large, complex algorithms people have always hoped for. “We still have a long way to go, we still need to do this at scale,” Newman acknowledges. “But the first time we pushed the button on this Willow chip and I saw the lattice getting larger and larger and the error rate going down and down, I thought ‘Wow! Quantum error correction is really going to work…Quantum computing is really going to work!’”

Why error correction is quantum computing’s defining challenge
Mikhail Lukin, a physicist at Harvard University in the US who also works on quantum error correction, calls the Google Quantum AI result “a very important step forward in the field”. While Lukin’s own group previously demonstrated improved quantum logic operations between multiple error-corrected atomic qubits, he notes that the present work showed better logical qubit performance after multiple cycles of error correction. “In practice, you’d like to see both of these things come together to enable deep, complex quantum circuits,” he says. “It’s very early, there are a lot of challenges remaining, but it’s clear that – in different platforms and moving in different directions – the fundamental principles of error correction have now been demonstrated. It’s very exciting.”



