Einstein’s equations of general relativity are like the Himalayan mountains – beautiful and majestic when viewed from a distance, but slippery and full of crevasses when explored up close. Of those who venture into them, not everyone comes back alive. A set of 10 independent, nonlinear partial differential equations, Einstein’s equations relate the energy and matter in a region of space to its geometry. Astonishingly simple when expressed in the geometric, coordinate-independent language of tensors that Einstein ultimately hit upon, the equations – when applied to real situations – unfortunately become coupled beasts unlike anything physicists had tamed since the days of Newton.

Einstein’s equations of general relativity can be solved exactly only in a handful of cases – with one of the first such solutions, and perhaps its most famous, being that derived by the German astronomer Karl Schwarzschild in 1916 for the simple case of a static, spherical, uncharged mass in a vacuum. Schwarzschild’s assumptions, and his mathematical wizardry, reduced the Einstein equations to a single, ordinary differential equation that he was able to readily solve, though even the master himself was surprised at the possibility of an exact solution. The “Schwarzschild solution” leads naturally to the concept of a black hole (see “Black holes: the inside story”), although Schwarzschild himself never grasped the significance of the singularity in his solution, dying four months later on the Russian Front during the First World War. Even Einstein thought the Schwarzschild singularity – the radius where the solution is invalid because of division by zero – was physically meaningless, and it was only decades later that the depths of the Schwarzschild solution were plumbed in general relativity’s first golden age, which ran from about 1960 to 1975, by Roger Penrose, Kip Thorne, Stephen Hawking and many others besides.

As theories go, general relativity has been a great success. Most famously, its early approximate solutions accounted for a well-known discrepancy in the orbit of the planet Mercury that could not be completely accounted for using classical Newtonian physics, yielding a value for the difference that agreed spot-on with astronomical measurements. Einstein’s equations have also predicted that light bends in a gravitational field and even that radar signals are delayed when bounced off one of our solar system’s inner planets. However, these successes are all based on the “post-Newtonian” approximation of the full Einstein equations, where speeds are small compared with that of light and gravitational fields are weak. Einstein’s general relativity has never been tested in the vastly different “strong field” regime.

Thanks, however, to fast and powerful supercomputers, physicists can now crunch by brute force through Einstein’s equations using advanced computational algorithms. Using what is known as “numerical relativity”, we can explore physical regimes where space–time is far from the simple, flat, 4D world of special relativity, obtaining exact solutions even where gravity is strong and so space and time are stretched and twisted. Indeed, theorists have already made some major breakthroughs in solving Einstein’s equations with computers, leading to specific predictions that astronomers can now test.

With analysis and observation converging, new insights have been gained into some of the most energetic and spectacular phenomena in the universe that are, in turn, pushing the numerical relativists to study even more complex systems, in realms that physics has never delved before. These new methods have uncovered the possibility of “rogue” black holes, kicked from their galactic lairs to rush silently through intergalactic space. They have even become a tool for understanding the dynamics of black-hole pairs, for probing the equation of state of neutron stars, and for helping us to design future space-borne detectors for hunting gravitational waves – tiny oscillations in the fabric of space–time itself. It is, it has been said, general relativity’s new golden age.

Subtle and malicious

Relativists had been trying since the 1960s to numerically solve Einstein’s equations, but extracting the physics from even simple cases proved exceedingly difficult. Early on, theorists formulated clever ways to package the problem for a computer by dividing 4D space–time into a stack of 3D surfaces labelled by a time parameter. But those using such approaches found that their computer programs crashed after becoming unstable or suffering large numerical errors – even in simple cases such as two black holes colliding head-on. It seemed that Einstein might have been wrong after all: the Lord was both subtle and malicious.

The problem gained added urgency in the 1990s as the US began planning the Laser Interferometer Gravitational-Wave Observatory (LIGO) – two giant interferometers in Washington and Louisiana that eventually began taking data in 2002 in the still-ongoing quest to detect gravitational waves. In order to extract the tiny gravitational-wave signals from background noise, designers needed to know the exact form of gravitational waves that hopefully would wash over the apparatus – in particular their amplitudes and frequencies – because this would determine precisely by how much, and how fast, the arms of the interferometer would change in length. But at the time, theorists investigating the astrophysical phenomena that were expected to generate such waves, especially two black holes merging, could only help LIGO’s designers in general terms. “In the 1990s the Einstein equations for two black holes colliding became the holy grail of general relativity,” recalls Laura Cadonati, a gravitational phenomenologist at the University of Massachusetts at Amherst, who applies numerical results to astrophysical systems.

The problem was not simple. In addition to producing instabilities, the programs ultimately needed to span a time period long enough to cover the last few inspirals of an orbiting black-hole pair, their merger and subsequent settling (called the “ringdown”) of the final black hole. The relativists were stuck: their computers, and especially their methods, could address various parts of the problem – in two spatial dimensions, or just up until the merger – but not for an entire event that could occur in the real universe.

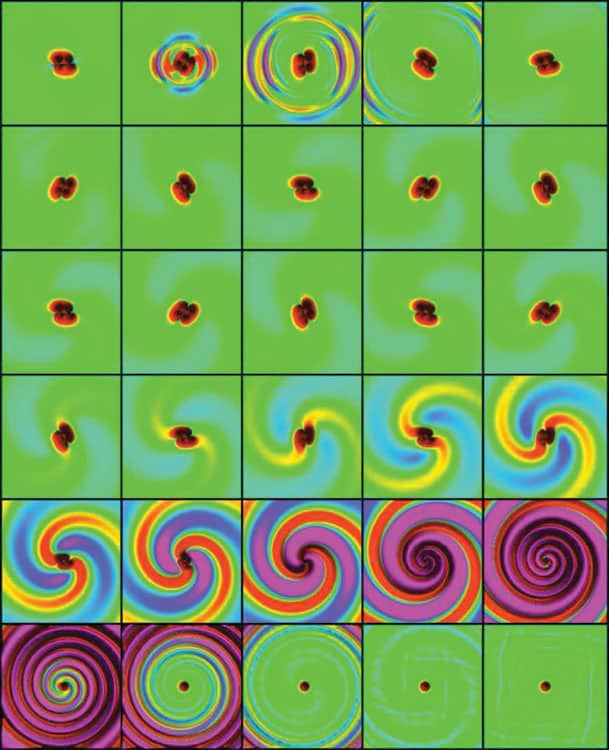
Then, in 2005, a postdoc at the California Institute of Technology, working largely on his own, stunned the relativity community with a stable numerical simulation of two equal-mass, initially non-spinning black holes from their single, last orbit to the ringdown (figure 1). Frans Pretorius formulated the Einstein equations in a different way from how others were doing it, leaving him with fewer and slightly simpler equations to solve. His trick was to use coordinates that made the partial differential equations describing the changes in space–time identical to the standard wave equation that physicists knew and loved so well.

“Several things came together,” says Pretorius, recalling his triumph, adding that “there was luck involved, too”. Pretorius eventually spent two years on the problem, which he says involved helpful insights from colleagues including David Garfinkle and Carsten Gundlach, lots of coding elbow grease and a supercomputer program that ran off-and-on for two months. It was, for him, “pure agony”.

Pretorius, who is now at Princeton University, found that the merger yielded a single spinning black hole weighing 1.90 times the mass of one of the initial black holes. It had an angular momentum of about 0.70 times the square of the final black-hole mass, and roughly 5% of the total initial mass was radiated away as gravitational waves – figures that no-one had calculated before. Pretorius also computed the detailed waveform of the emissions in terms of a scalar function that classifies space–time, which can be related to the time-varying amplitude of a gravitational wave and, in turn, the minute fractional changes in the length of the arms of a gravitational-wave detector. As his program kept going without crashing, Pretorius thought “Oh God, this can work” until he experienced what he says was “instant gratification with an endorphin rush” when it was finally complete. Pretorius’s result, now known as the generalized harmonic formulation, broke the field’s log jam.

Later that year researchers at the University of Texas at Brownsville and NASA’s Goddard Space Flight Center independently developed another technique for black-hole numerical solutions, called the “moving puncture” method, that was promptly adopted by much of the community because it was more accurate, albeit at the expense of greater computational complexity. A rough 2D analogue is a model of space–time where two parallel sheets of cloth, each with a disc removed at a black hole’s event horizon, are sewn together around the disc perimeters. These punctures – the interiors of the black holes removed from the computational domain – then move around the lattice grid that represents space–time as the computation progresses, revealing the motion through time of the black holes’ horizons.

“Very quickly everyone got it, along both approaches,” says Luis Lehner of the Perimeter Institute for Theoretical Physics in Waterloo and the University of Guelph, both in Canada. The challenge now for Lehner and others was to find out “how fast can we get the answers out, and where can we go looking for the unexpected to further our understanding and raise further questions”. Researchers at Goddard soon computed the merger of unequal-mass black holes for the first time, studying in the process the accompanying recoil of the final black hole. The result was found to depend only on the ratio of the masses of the merging black holes, not their individual values, making the calculated gravitational waveform applicable to a range of astrophysical situations. The overall energy released in the process – and the time taken for the two holes to merge – is proportional to the total mass, meaning that the merger could briefly outshine all the stars in the universe combined.

These first simulations were of black holes that were initially not spinning before they collided, and it was not long before a research group at the University of Texas at Brownsville carried out the first investigation of the merger of spinning black holes – both with their spin axes aligned and misaligned. Indeed, continuing advances in technique and computing power allowed researchers to calculate what happens as these spinning black holes collide over a range of different orbits. Theorists and experimentalists began to mix, not quite as cats and dogs but, as Cadonati politely puts it, “to improve the potential of gravitational-wave science and how that matches with astrophysics” (figure 2). The former slaved away plugging actual numbers into their elegant equations, while the experimentalists fished out their postgrad notes on tensor analysis.

Black holes get a kicking

In 2007 numerical relativists found a surprise emerging from their simulations. Straightforward considerations of the mechanics of unequal-mass, inspiralling black holes suggested that, in order to conserve angular momentum, the gravitational radiation they produce will not be emitted equally in all directions. The implication was that the final black hole produced when the two bodies collide ought to have some linear momentum relative to the centre of mass: they will in effect be given a “kick”. But full simulations by Manuela Campanelli and colleagues at the Rochester Institute of Technology in New York, and then José González and co-workers at the University of Jena in Germany, showed that this momentum was far from small: the final black hole could have a speed of up to 4000 km s^–1 for holes spinning in opposite directions. (Stars near our own Sun, in comparison, move at barely a few tens of kilometres per second.)

Recently, even higher speeds, or “superkicks”, have been found of up to 15,000 km s^–1 , with some theorists suggesting that speeds three times higher still – or 15% of the speed of light – might be possible. Because such kicks would be greater than the escape velocity of any galaxy, the finding opens up the possibility of black holes living in galactic halos far away from their galactic nucleus, or perhaps even single, rogue black holes cannonballing through the universe. These holes would be largely invisible until they roamed through, say, the Oort cloud of comets that lies within about a light-year of the Sun, when it might be possible to detect them through tiny, mysterious shifts in the movement of comets or tiny planets. In the unlikely event that a rogue black hole should barrel through our solar system, we would quickly be relieved of all our earthly worries.

Less catastrophically, superkicks have implications for those searching for gravitational waves. Black holes ejected from globular clusters – collections of stars that orbit galactic cores as a satellite – would lower the subsequent merger rate for black holes remaining in the cluster, and so would reduce the number of gravitational waves expected at detectors. Large recoils would also remove high-velocity black holes, and could constrain how early in the universe small seed black holes would have merged into larger black holes.

A spectroscopy of the heavens

Numerical relativity has played a key role as well in the search for gravitational waves, even if the added complication of rogue black holes is probably the last thing that those involved need, given that detecting these tiny ripples is hard enough as it is. The problem is that although sources such as binary stars radiate enormous amounts of energy as gravitational waves – at rates of 10²⁸ W or more – by the time those waves reach Earth, their deviation from flat space will alter the length of an interferometer’s arm by a factor of only 10^–18 , or even less. Gravitational-wave interferometers, such as LIGO in the US, VIRGO in Italy, TAMA in Japan and GEO600 in Germany, must therefore detect tiny length differences when a gravitational wave washes over them.

Gravitational-wave hunters are especially interested in stellar-mass black holes and supermassive black holes because they produce waves at frequencies of 10–10,000 Hz when they merge – exactly the range that ground-based detectors such as LIGO are most sensitive to. But because the Earth is a shaky place, the number crunchers need some guidance as they try to distinguish the minuscule fluctuations of gravitational waves from seismic shifts and even passing trains. Knowing what waves to expect helps a great deal.

Towards this end, the Numerical Injection Analysis project (NINJA) was started in 2008, bringing together numerical-relativity groups and data-analysis teams from 30 institutions across the globe. Relativists provide waveform templates in the form of ASCII data files that specify their predictions for the time-varying weights of the waves when decomposed into spherical harmonics. These must cover the broad parameter ranges of black-hole mergers – mass ratios, spins and eccentricities – that are most likely to occur. Even the simple case of a binary black hole has 17 variables, or degrees of freedom, among the source and detector configurations.

But the methodology works. On 16 September 2010, for example, detector scientists were alerted to the arrival of a “chirp” signal only minutes after its arrival. After analysing it, members of the LIGO and VIRGO collaborations reported the discovery of gravitational waves, seemingly from a neutron star spiralling into a black hole. They even wrote up a paper about it – only to be told that the event was a “blind injection” of fake data put in by project insiders. The researchers had been told of such a possibility beforehand, and although their paper went unpublished, their techniques were validated, as was their vigilance.

While the results from numerical relativity have gone some way towards helping gravitational-wave researchers, they could play a still bigger role in upcoming missions, notably the Advanced LIGO facility – an upgrade to LIGO that will search a volume of space 1000 times bigger than the existing facility and is expected to begin science operations in 2015. The first-generation LIGO had about 10,000 expected waveforms in its database, while Advanced LIGO will have about 100,000. Comparing data to such a large number of possibilities is, needless to say, computationally intensive.

Indeed, in January the National Science Foundation awarded Syracuse University in the US almost $800,000 to build a supercomputer that will eventually have almost 500 terabytes of storage for just this purpose. “It’s the Advanced LIGO detectors that people are looking to really open up the field of gravitational-wave astronomy,” says Syracuse’s Duncan Brown, who is a member of the LIGO collaboration. Syracuse’s machine will be one of three such devices designed for the purpose, the others being at the University of Wisconsin–Milwaukee and at the Albert Einstein Institute for Gravitational Physics in Germany.

The details of gravitational waveforms depend on many factors. Relativists have studied systems that are more complex than binary black holes, such as a neutron star colliding with a black hole, or pairs of neutron stars, and recently have even moved on to inspiralling binaries with external magnetic fields and their surrounding plasmas, finding that these can lead to powerful jets that could be observed with X-ray telescopes. These interactions require the solution of the full Einstein equations coupled with hydrodynamic equations for the plasma, which in turn require an equation of state for the neutron star. Gravitational waves might therefore someday help us to distinguish between different models of neutron stars – a kind of “spectroscopy of the heavens”.

Adding yet another facet to the problem, Yuichiro Sekiguchi and other theorists from Kyoto University in Japan recently studied the behaviour of a neutron-star pair described by Einstein’s equations coupled with hydrodynamic equations, while incorporating the cooling of the final hypermassive neutron star by neutrino emission. They found both the gravitational-wave spectrum and the luminosity of neutrino emissions from the final star; the latter could be higher than even that seen in supernova explosions that already shine bright in ordinary heavenly light. Future astronomers will view all of these extreme events with three eyes: via gravitational waves, electromagnetic waves and neutrino bursts.

Scale me up

Picking out the best details will require a third generation of gravitational-wave detectors. With the existing LIGO detector, the gravitational waves of a binary neutron star are only in a detectable band for about 25 s (and about 1 s for a binary black-hole system). Advanced LIGO could detect a gravitational anomaly lasting about 1000 s, although this still only represents the last thousand seconds of a coalescence that has been billions of years in the making.

The future lies in scaling up. The proposed Laser Interferometer Space Antenna (LISA) system – three satellites that would be five million kilometres apart in a planetary-like orbit around the Sun – would see gravitational waves (in the band 0.1 mHz – 1 Hz) that could last hours, weeks or even months, out to redshifts of 5–10. Unfortunately, LISA’s realization is currently uncertain; NASA bowed out of the project this year and, although the European Space Agency said it might launch a smaller version, no decision has yet been made.

European researchers are, however, planning to build what is dubbed the Einstein Telescope – a gravitational-wave detector that would be built a few hundred metres below ground with two arms each a massive 10 km long. It would be 10 times more sensitive than even Advanced LIGO and able to access a million times the space-volume of current ground-based detectors. Although today’s best numerical simulations are good enough for the accuracy needed for such a detector, studying the entire 9D parameter space of even a black-hole binary without matter could take another decade.

Still, as with many breakthroughs, today’s new golden age of relativity is opening vast unexplored areas of physics, with many surprises surely to come. It might be almost 100 years since Einstein came up with his equations, but his gift is giving still. Today is a good time to be in the gravity business.

At a Glance: Numerical relativity

• Einstein’s general theory of relativity describes the relationship between the energy and matter in a region of space and its geometry, and has passed all experimental tests to date
• Unfortunately, Einstein’s equations are fiendishly complicated and can be solved exactly in just a handful of cases
• Powerful supercomputers can, however, crunch through the equations using brute force
• This approach, known as “numerical relativity”, has been used to study how black holes merge, showing that in some cases they might create rogue holes rushing through intergalactic space
• Numerical relativity is also helping researchers seeking the signatures of gravitational waves

Black holes: the inside story

Amazingly, given their heft and their surly reputation, black holes are among the simplest objects in the universe and can be fully characterized by just three terms – their mass M, charge Q and angular momentum or “spin” J. Indeed, the Indian Nobel-prize-winning astrophysicist Subrahmanyan Chandrasekhar, who first predicted that they might be created when large stars die, called black holes “the most perfect macroscopic objects there are in the universe”. Black holes come in three main varieties:
1 solar-mass black holes, with masses about 3–30 times the mass of the Sun;
2 intermediate-mass black holes with about 100–10,000 solar masses, such as (almost all astronomers would now agree) the Hyper-Luminous X-ray source (HLX-1), which lies in a galaxy 290 million light-years from Earth;
3 supermassive black holes that lord over the centres of galaxies, with millions to billions of solar masses.

In terms of spin, at one extreme is a Schwarzschild black hole, which has zero spin, while an extreme Kerr black hole, carrying no charge, has the maximum spin allowed by general relativity of GM²/c, where G is the gravitational constant and c is the speed of light.

More about: Numerical relativity

J Centrella et al. 2010 Black-hole binaries, gravitational waves, and numerical relativity Rev. Mod. Phys. 82 3069
M Hannam 2009 Status of black-hole-binary simulations for gravitational-wave detection Class. Quant. Grav. 26 114001
D Merritt and M Milosavljevic 2005 Massive black hole binary evolution Living Rev. in Relativity 8 8
F Pretorius 2009 Binary Black Hole Coalescence, in Physics of Relativistic Objects in Compact Binaries: from Birth to Coalescence ed M Colpi et al. Astrophysics and Space Science Library vol 359 (New York, Springer)