Exactly a year ago, researchers at MIT reported on observing superconductivity in twisted bilayer graphene – a new experimental platform engineered on two misaligned graphene layers – at “magic angles” near 1.1°. The origin of these angles was a mystery, however. A team at Harvard University has now shown that they appear to be fundamentally connected to quantum Hall wave functions.
Graphene is a flat crystal of carbon just one atom thick. When two such sheets are placed on top of each other with a small angle misalignment, they form a Moiré pattern. More surprisingly still, at the twist angle of 1.1°, the material becomes a superconductor (that is, it can carry currents with no losses) at 1.7 K. This effect disappears at slightly larger or smaller angle twists.
This result, obtained by Pablo Jarillo-Herrero and colleagues at the Massachusetts Institute of Technology (MIT), kick-started a flurry of activity in the field of “twistronics”, which is a fundamentally new approach to device engineering. Here, the weak coupling between different layers of 2D materials, like graphene, can be used to manipulate the electronic properties of these materials in ways that are not possible with more conventional structures – by varying the angle between the layers. After this discovery, researchers also reported on superconductivity and correlated (Mott) insulation in other similar systems – such as Moiré superlattices of three graphene layers on 2D boron nitride or twisted four layers of graphene.
Moiré superlattices
“The main idea in twistronics is to play with different crystal cell sizes and symmetries by introducing Moiré patterns,” explains Alex Jura Kruchkov, who led the present research effort. “Recently, for example, it was shown that the Moiré patterns in graphene sheets twisted to 30° form a 12-fold-symmetric quasicrystal – a type of atomic ordering ‘forbidden’ in old-school crystallography.”
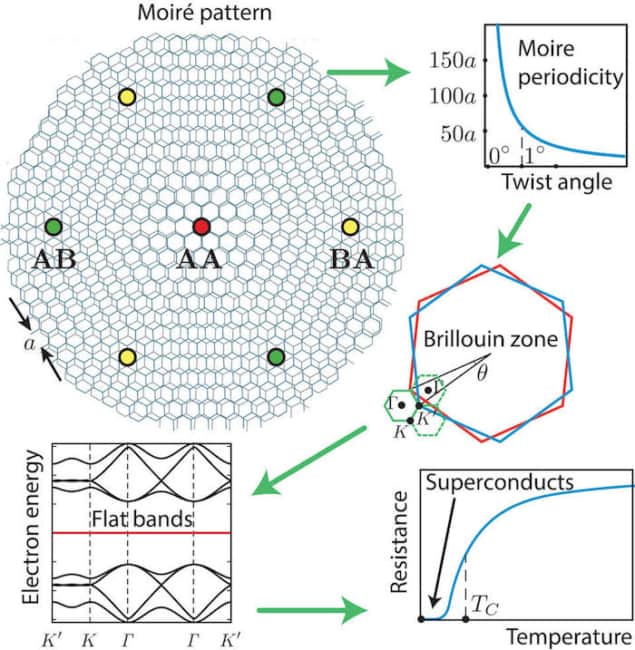
The crystal structure of a single layer of graphene can be described as a simple repetition of carbon atoms, which is known as its unit cell. In a Moiré superlattice of two graphene layers stacked on top of each other, this unit cell expands to a huge extent, as if the 2D crystal was artificially “stretched” a hundred times in all directions. This stretching dramatically changes materials interactions and properties, and simply varying the angle between 2D material layers changes its electronic band structure. At small twists, the Moiré graphene superlattices can even be switched from fully insulating to superconducting, as Jarillo-Herrero’s team discovered.
Flat bands are key
Researchers first introduced the concept of magic angles back in 2011 when studying the electronic structure of small-angle twisted bilayer graphene and reported on gapless band flattening at these angles. Since flat band engineering is very challenging, they were happy to simply observe this effect – which was considered as being a lucky feat of material engineering.
“The emergence of flat bands in electronic band structures is an intriguing phenomenon in itself. In a simple, non-interacting, description, the flat band state means that an electron is dispersionless – that is, it does not matter how much energy you can pump into it, it will not move. Correlated electron behaviour appears when we add interactions, however.”
‘Magic-angle graphene’ behaves like a high-temperature superconductor
There are only a few systems with flat bands – and scientists are looking for more because these bands promote exotic topological phenomena together with strongly-correlated states of matter. “Currently, the nature of superconductivity in twisted bilayer graphene is still being debated, but it is clear that the flat bands emerging at the magic angles play the fateful role,” says Kruchkov
One of the best-known examples of flat bands are the so-called Landau Levels in the quantum Hall effect, he explains. Introduced by Lev Landau at the beginning of the 20th century, the flat bands of electrons in an applied magnetic field were essential in explaining the integer quantum Hall effect, which is a topological phenomenon in flat (2D) systems in which the transverse (Hall) conductance is fundamentally quantized in units of e2/h (e being electric charge and h the Planck constant).
In their work, Kruchkov and colleagues showed that it is possible to create perfectly flat bands in twisted bilayer graphene. “Under this condition, the electron wave functions map exactly to the lowest Landau level in the quantum Hall effect (‘on the torus’),” explains Kruchkov. “In other words, it is as if the magic-angle Moiré patterns create artificial magnetic fields that the electrons ‘sense’.”
“Not just a matter of engineering material properties”
“At small twists the Moiré patterns are huge, so electrons effectively ‘forget’ about the underlying (small) graphene lattice and travel under effect of the larger and ‘calmer’ Moiré lattice,” he tells Physics World. “This is called the continuum model and it can be parametrized by the values of microscopic interactions at different atomic stackings in the bilayer. If there is no twist in the graphene bilayer, it prefers the energetically more favourable Bernal (AB) stacking. What happens under twists is that the Moiré pattern introduces both AB-stacked and AA-stacked regions.”
‘Twistronics’ tunes 2D material properties
Since they are energetically preferable at smaller twists, regions of AB stacking dominate and regions of AA stacking shrink, he explains. This dramatically suppresses the value of AA interactions compared to AB ones. In their discovery, the Harvard researchers show that if the AA interactions are fully “switched off”, the electron bands become perfectly flat exactly at the magic angles – reminding us of a perfectly flat Landau level.
“The emergence of these flat bands is thus not just a matter of engineering material properties – as previously thought – but is related to the flatness of the lowest Landau level and has deep hidden connections to quantum Hall wave functions on the torus,” says Kruchkov.
“Finding such a surprising link between two seemingly different subfields of physics is unusual. At the heart of our work is a fundamental model with perfectly flat bands that induce robust periodicity in the magic angles. In fact, if parametrized as α =(material constant)/(twist angle),the magic angles in our model follow a remarkable sequence with the robust asymptotic periodicity Δα= 3/2, something that has never been reported on before.”
The Harvard physicists also show that the principal magic angle can be very precisely calculated and that its value is the same as that reported in experiments. They believe that exotic magic-angle phenomena could occur in other van der Waals layered devices, and they are now actively investigating these systems.
Full details of the research are reported in Physical Review Letters.