A short-lived experiment…
By Hamish Johnston
Here’s a question for you — what is the easiest way to move a large rug?
The answer, according to carpet fitters — as well as two papers in Physical Review Letters — is to create a “ruck” and then push in along the rug (see photo above).
The reason, apparently, is that the ruck is quasi-static, which means that it can be moved easily by a series of gentle pushes that don’t take it very far out of equilibrium
I thought I would try it for myself, but the only rugs I could find were in the main entrance to Dirac House and there was too much foot traffic to do the experiment safely!
If you want to read more about rucks, check out Statics and Inertial Dynamics of a Ruck in a Rug by Dominic Vella, Arezki Boudaoud Mokhtar Adda-Bedia as well Shape and Motion of a Ruck in a Rug by John M. Kolinski, Pascale Aussillous and L. Mahadevan.
The first paper begins with an investigation of the conditions needed for a static ruck to persist — rather than flatten out — once it’s been created. The team derived an equation describing the transition and tested it experimentally using several “rug” and “floor” materials, incluing a real rug on a wooden floor.
The equation, which had to be solved numerically, did a pretty good job of predicting which rucks survive and which collapse.
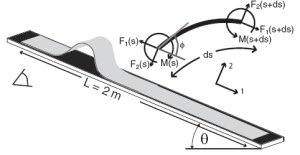
Ruck on a roll
The second paper looks at rucks “rolling” downhill by placing a thin latex rug on an inclined plane. The team found that a static ruck will begin to roll when the plane is tilted above a critical angle. It will continue to roll until the angle is reduced to a second critical angle — which is smaller than the first angle.
From this, the team concluded that the coefficient of static rolling friction is greater that the coefficient of dynamic rolling friction.
You’re probably wondering what they mean by a rolling ruck?
To show that the ruck was rolling — rather than sliding — the team followed the paths of points on the rug as the ruck moved through and found that they move on a cycloidal tragectory. In other words, the points moved as if they were on the rim of a rolling wheel.
You’re probably also wondering why PRL has published two papers on rugs?
According to the first paper rug rucks have “long proved to be a useful analogy
in explaining a range of important physical phenomena”. These include dislocations in crystalline materials as well as wrinkle-drive motion, which has been observed in living organisms including inchworms.