Atoms subjected to intense, ultrashort pulses of laser radiation ionise in surprising and, as yet, not wholly understood ways, explain Pierre Agostini and Guillaume Petite

Technology is set to yield, in the near future, unprecedentedly short (10–14 s) and intense (1017–1019 W cm–2) light pulses. Such intensities have in the past been the preserve of the gigantic systems associated with laser fusion research but a considerable reduction in system size has made them available to the atomic physicist. Experiments using such lasers are just beginning and there have been as yet few investigations at intensities beyond 1014 W cm–2. Nevertheless these have already provided some delightful surprises.
One is that, contrary to general belief, atomic structure does still play an important role at these intensities – thus such pulses provide a powerful tool to investigate atomic distortions in intensity ranges where standard techniques fail. In a sense, ultrashort pulses allow us to take snapshot views of the atoms within the laser field. For instance, recent experiments on multiphoton ionisation have revealed giant energy shifts in atoms subjected to 5 × 1013 W cm–2.
The atomic energy level structure is governed, of course, by the interaction between the electron and the nucleus. For the simplest atom, hydrogen, for instance, this structure is very simple: in the non-relativistic limit, the energy levels depend only on the principal quantum number n, as (–1/2n2), and occur closer and closer to each other as n goes to infinity. In this case the energy does not depend on angular momentum, states with the same principal quantum number and different angular momenta being degenerate. At low intensities the light induces transitions between unperturbed atomic states.
At high intensities, in contrast, the interaction between the electron and the nucleus may be dominated by the interaction between the electron and the light field. The energy level structure is therefore, in general, strongly distorted and the degeneracy is suppressed. In any case, the electron interaction with the laser light can no longer be considered as a small perturbation of the atomic system. The system, atom and light, must be treated as a whole. Thus this physical domain is often characterised as nonperturbative. It is very likely that contiguous disciplines such as plasma physics or surface physics will soon benefit from developments in this regime, a prospect that brightens the outlook of many a research group.
Multiphoton physics
Elementary quantum mechanics tells us that transitions between two bound states give rise to a discrete absorption/emission spectrum, whereas transitions to unbound or free states (ionisation) yield a continuous spectrum. Energy conservation in ionisation determines the kinetic energy of the outgoing electron Ek = hv – E1 where hv is the energy of the photon of frequency v and E1 is the binding energy of the initial atomic state. Another class of processes is formed by the transitions involving the simultaneous absorption of several photons. Such multiphoton transitions allow one, in principle, to ionise an atom with light corresponding to photon energies smaller than E1 provided photons N are absorbed simultaneously. Energy conservation then yields an electron with kinetic energy Ek = Nhv – E1.
Multiphoton ionisation (MPI) processes are observable only with intense pulsed laser sources once N is larger than two. If the intensity is not too high, MPI processes of order greater than two can reasonably be described within the framework of time-dependent perturbation theory, to the lowest ‘non-vanishing’ order. This means that, if the absorption of a minimum number of photons N is required, for energy conservation, to ionise the atom, perturbative solutions of the Schrodinger equation up to order N must be found to obtain the ionisation rate. Such an approximation is valid if the shifts and broadenings of atomic states can be neglected, or at least for all ‘non-resonant’ transitions observed with intensities up to 1011–1012 W cm–2. By ‘non-resonant’ we mean transitions in which the atom ground state is coupled to the continuum without going through some intermediate excited or ‘resonant’ state. Under this approximation, the ionisation rate scales as the laser intensity to the power N.
In fact, part of this description breaks down as soon as the intensity I is around 1011 W cm–2 as immediately revealed by electron energy analysis (figure 1a). Atoms can absorb not only the N photons necessary for ionisation but also a few more (S) which are used to accelerate the electrons, increasing their kinetic energy by Shv. The electron energy spectra display a number of lines of small and decreasing amplitude, separated by the photon energy. The production rate of each ‘peak’ scales as IN+1, IN+2 . . . This process, known as above-threshold ionisation (ATI), is a correction to MPI of the lowest possible order and was first detected at Saclay.
Moving to high intensities
Things become more complicated as the intensity is increased (>1012 W cm–2) because it is not then possible to assume that transitions occur between unperturbed states. Suppose one electron is orbiting around the nucleus. When the electromagnetic field (produced by the laser) is turned on, the Lorentz force perturbs the electron motion and therefore its energy. Changes in the energy of atomic bound states then induced are known as AC-Stark effects because of their relation to the Stark effect.
Three situations might occur: (i) if the light or field frequency v is close to the energy difference between the initial state and some state to which it can be coupled, the two states are ‘mixed’ and their energies are shifted by this mixing. If v is smaller than their energy difference then the two states are pushed apart, and vice versa if v is larger than their energy difference. (ii) If v is small compared to any atomic energy difference then the state the electron occupies is repelled by the coupling to the other states. This is usually the case for the atom ground state if v is in the red or infrared region of the electromagnetic spectrum, and the ground state is down-shifted in energy by a small amount. (iii) If v is large compared to any atomic energy difference (for instance for states whose energies lie close to the ionisation threshold) then the shift is always positive and large. In this case there is a simple classical interpretation of the shift: the motion of the electron can be thought of as a slow orbiting motion around the nucleus superposed by a fast ‘quiver’ motion driven by the electromagnetic field around the average orbit. The latter has an average kinetic energy which adds to the electron energy. Its value in eV is easily computed from classical mechanics, given by EQ = 0.94 × 10–13 I λ2 where I is the intensity in W cm–2 and λ the wavelength in μm. This energy is known in the literature as the quiver energy or the ponderomotive potential. The same interpretation does not however hold for strongly bound electrons since the orbital motion is then faster than the oscillatory motion.
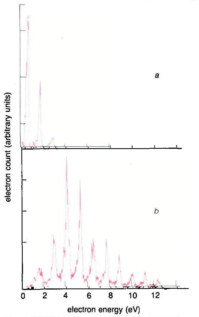
Figure 1
(a) Photoelectron energy spectrum from multiphoton ionisation of xenon (ionisation potential 11.13 eV) by 1.17 eV photons (intensity = 2 × 1012 W cm–2). The leftmost peak is produced by 11 photon ionisation (the minimum required by energy conservation). The next two peaks, due to 12 and 13 photon ionisation, are separated by an energy equal to the photon energy (above threshold ionisation); (b) As in (a) but with a five times larger intensity (1013 W cm–2). Ten photons are absorbed above the ionisation threshold. The strong electromagnetic field has distorted the atomic structure; the first peak is totally suppressed while the most probable one is the fourth one.
Stark shifts as described above become crucial once the intensity is above 1012 W cm–2 and have two consequences: first, the small down-shift of the ground state and the large up-shifts by the quiver energy of the states close to the continuum causes the ionisation potential to be apparently increased by a little more than the quiver energy. For intensities of 1013 W cm–2 and a wavelength of 1 μm this increase is about 1 eV, that is, the energy of one photon. Therefore ionisation of the atom requires absorption of at least (N+1) photons. This leads to spectra such as those in figure 1b: the first peak which would correspond to N photon ionisation is missing; the second one which corresponds to (N+1) photon ionisation is strongly suppressed while the most probable peak corresponds to an (N+2) photon transition.
A second consequence is that the energy of some state of the atom may be shifted via the Stark effect in such a way that it becomes equal at some intensity to the energy of an integer number of photons. The transition probability is then boosted if this resonance condition is met. For instance if one keeps the intensity constant and scans the light frequency, the ionisation signal is strongly enhanced in a small region of frequency; if the frequency is kept constant and the intensity scanned, then a similar enhancement is seen around the intensity value which Stark-shifts the state into resonance. In a real focused laser beam, however, this is unnecessary as all intensities between zero and the maximum are already present. If, in some part of the focused region, the intensity causes resonance, then more electrons will be produced there because the probability is much higher. The electrons produced in this region of the beam have an energy Ek = (N+S)hv – (E1+EQ(IR)) where IR is the resonant intensity: neglecting the small shift of the ground state, the ionization potential E1 appears to be increased by EQ(IR). As a consequence, the electron energy spectrum should show a bump at the energy Ek, which is shifted by EQ from (N+S)hv – E1. But this is not what is shown in figure 1b. No extra bumps are detected and the peaks are exactly at (N+S)hv – E1, although the intensity is high enough for the first peak to be suppressed, and shifts of the order of the separation between two adjacent peaks should be observed.
After the first observation at the FOM Institute in Amsterdam, it took some time to understand that this discrepancy occurs because the electron energy was measured outside the laser beam. This apparently innocent circumstance has drastic consequences for the measured energy. The best way to see this is the following: the photoelectrons are created inside the laser beam with both a translation energy Ek and a quiver energy EQ (equivalent to saying that the ionisation potential is increased by EQ). As an electron travels to the detector which lies outside the beam, it has to cross the region where the intensity is changing rapidly, from the peak intensity to zero over typically 10 μm. In doing so it is subjected to the Lorentz force which depends both on time and space. Classical electrodynamics shows that this force has a component proportional to the gradient of the electromagnetic field. This ‘ponderomotive force’ tends to accelerate the electron towards the low intensity regions, that is outside the focused beam. Furthermore, a classical calculation shows that the total work done by this force along the electron trajectory is precisely EQ. In fact, the quiver energy acts as a potential (hence its other name, the ponderomotive potential) from which the ponderomotive force is derived. Again from classical mechanics, the change in kinetic energy is shown to be equal to the variation of the potential, which is exactly EQ since the quiver energy is zero outside the beam. Hence, the electron energy outside the beam is just (N+S)hv – E1 no matter what value the initial quiver energy of the photoelectron has (provided S is sufficiently large, that is for the peaks which are not suppressed).
Short sharp pulses
This is where ultrashort pulses are really useful. If the pulse duration is shorter than the time taken by the electron to leave the beam (which depends on the initial electron velocity and the size of the beam) then some or all of the quiver energy is lost. Changing the laser pulse from 136 ps to 50 ps was sufficient to allow us to observe the predicted shifts in the energy peaks (see figure 2). The slow electrons (low energy) are shifted more than the fast ones (high energy) and the shift depends on the ratio of the pulse duration to the electron exit time. With this observation, it was easy to figure out what would happen if, instead of a 50 ps pulse, a much shorter pulse (1 ps or less) was used: the pulse would be much shorter than all exit times and all the peaks would be shifted by the same amount, EQ.
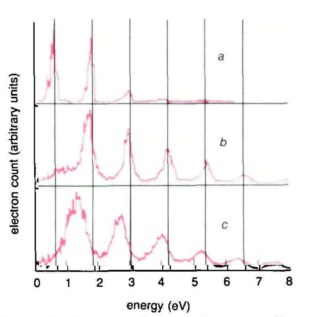
Figure 2
Photoelectrons are produced with both translation energy and quiver energy. (a) Long-pulse (136 ps), low-intensity reference spectrum; (b) In long pulses (136 ps) the quiver energy is converted into translation energy as the electron travels out of the laser beam and the peaks are not shifted even though some may be suppressed; (c) For short pulses (50 ps), part of the quiver energy is lost and the slower the electrons the more the peaks are shifted towards lower energies. Vertical solid lines show the expected positions of the peaks.
The technique of generating subpicosecond pulses is now well known: they are produced from CW, mode-locked ring cavities working in the colliding pulse, mode-locked mode. In such a laser, the gain is provided by Rhodamine dye, pumped by a CW argon ion laser, while the mode-locking is achieved by a saturable absorber. Two pulses counter-propagate within the ring cavity and collide inside the mode-locking dye jet, hence the name. Extremely short pulses (30 fs) with peak power of the order of a few kilowatts are produced at a repetition rate equal to the round-trip time of the pulse in the cavity. To reach the required intensities of 1014 W cm–2 the pulses are further amplified by YAG pumped amplifiers.
When subpicosecond pulses were used, the expected shifts, equal for all ATI peaks, were seen. Furthermore, the electron energy spectra displayed a number of extra substructures due (as we now know) to Stark-tuned resonances as explained above. When in fact this was first observed by a research group at Bell Labs, the explanation was far from obvious. From studies of resonant MPI by the usual technique of tuning the laser frequency, it was known that, as the intensity is increased, the resonances get broader and broader and, eventually, become undetectable. It was therefore generally taken for granted that atomic structure did not play any important role at high intensity. Of course, it took some more work to prove that the extra bumps, which looked like ‘noise’ in the first spectra, were due to atomic resonances.
Figure 3
(a) Photoelectron energy spectrum from multiphoton ionisation of xenon by 2 eV photons produced by a linearly polarised femtosecond laser: the main structure of three peaks separated by the energy of one photon is subdivided into more subpeaks that reveal the Stark induced resonances; (b) As in (a) but with circularly polarised light. Selection rules forbid the resonances, leaving only the main structure of the spectrum. This proves the atomic origin of the substructure in (a).
One crucial test was carried out by using circularly polarised light, in which all the photons have the same angular momentum, say +1, contrary to linearly polarised light which contains as many photons with an angular momentum +1 as photons with angular momentum –1. As a consequence, in an N photon transition with circularly polarised light, the atom which absorbs one unit of angular momentum with each absorbed photon, must increase its total angular momentum by N units. For instance, a six photon transition starting from an S state (l=0) must end in an I state (l=6) to conserve the total angular momentum. With circularly polarised light, all the extra substructures in the electron energy spectra were suppressed (figure 3b), leaving only the normal ATI ‘comb’. This not only confirmed the atomic origin of the resonances but also gave valuable information on the angular momenta of the resonant states. This and other tests led to the important conclusion that all multiphoton ionisation processes are resonant, whatever the atom and the laser frequency. Because of the combined effects of the shifts due to the loss of the quiver energy and the increase of probability due to the Stark-tuned resonances, the electron energy spectra taken with ultrashort pulses are an image of the ionisation probability as a function of intensity: such a function is clearly no longer a simple power law but a very complicated succession of maxima due to the resonances. This role of the atomic structure could only have been unveiled by intense ultrashort pulses and would have remained hidden in experiments using long pulses. Ultrashort pulses give a snapshot of the atomic energy levels as they are inside the light beam.
Of course, the larger the detuning from the energy of a given state and the energy of an integer number of photons, the higher the intensity needed to Stark-tune the state to resonance. Consider a small volume inside the focused laser beam where such an intensity is reached during the pulse. This could be thought to happen twice – once during the rise time and once during the fall time of the pulse – but, in fact, careful analysis shows that only the atoms in the region where the required intensity for a given resonance to occur is achieved around the maximum of the pulse will contribute to that resonance. Whatever the detailed mechanism, it appears as though the atom is itself picking the right intensity. The drawback is that substructures will occur at the same energy in the photoelectron spectra whatever the pulse peak intensity. Therefore, even though the peak intensity was varied to get information on the distorted atomic structure only one answer would come out of the type of experiments described above.
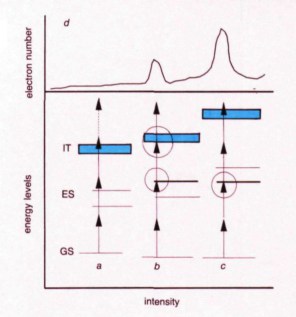
Figure 4
Stark-induced resonances. Energy levels are shown for three different electromagnetic field intensities: (a) at very weak intensity, the levels are not shifted and three-photon ionisation is energetically allowed. The dotted arrow indicates the absorption of one extra photon (ATI); (b) the intensity is sufficient to shift one of the excited states (ES) into resonance with the energy of two photons. The ground state (GS) and the ionisation threshold (IT) are shifted and the three-photon ionisation becomes energetically forbidden; (c) at even higher intensity the other excited state is shifted into resonance and the ionisation potential increases further; (d) the ionisation rate as a function of intensity: each time the intensity adjusts a resonance, the rate increases and then decreases as the intensity shifts the level out of resonance.
The way out of this dead end is to tune the laser. For a given resonance this changes the detuning and hence the intensity needed to Stark-tune the state into resonance. Following the position of the corresponding substructure as a function of the laser frequency will yield the energy of the state as a function of intensity, that is the dynamics of the Stark shifts at high intensity. Making the CPM laser tunable is very difficult, but fortunately, there is a trick to make life easier. If the output of the amplified femtosecond pulse is focused into a simple cell containing water then a white light continuum is generated through self-phase modulation. A narrow part of this continuum can be selected in an interference filter and subsequently amplified by another series of YAG-pumped dye cells. The experiment outlined above may be carried out for seven photon ionisation of xenon. By tuning the frequency as described, it was possible to change the detuning of six-photon resonances (6hv – ER, where ER is the unperturbed energy of a state which may be pushed into resonance by the Stark shift) by several electron volts. The electron volt is an energy unit which is really enormous by spectroscopic standards: it is equal to 8066 cm–1, the cm–1 being the standard unit in spectroscopy. Even in atomic units the electron volt is a huge quantity since the ionisation potential (half the atomic unit of energy) of hydrogen, for instance, is 13.6 eV. For a state which shifts as a free electron, an intensity of several 1013 W cm–2 is needed to push it upwards by 1 eV.
In the range explored in the experiment, the energies of all identified states depended linearly on intensity with a coefficient very close to the one found at very low intensity. This was very surprising since such a linear dependence was expected to break down rapidly as the intensity was increased. The experiment seems to show that atomic states dressed by a very intense electromagnetic field have a ‘simple’ behaviour although the reason for this is not yet fully understood.
Recent non-perturbative calculations show that there are three main intensity regimes: (i) very low – the shifts are predicted by second order perturbation and are linear in intensity; (ii) higher – the shifts are no longer linear and the states are strongly mixed energy levels; (iii) high – new states emerge which are strongly mixed too, even if they can be followed by continuity with a ‘naked’ state. Calculations suggest that these states may sometimes shift again linearly with intensity as in the first regime.
Obviously much more work is necessary to reach quantitative comparisons between theory and experiment. But, for the first time, it appears possible to study atoms dressed by very strong photon fields.
Two features round off this picture of MPI in ultrashort pulses. First there is the suppression of resonances under certain conditions. It is known that, by simultaneously exciting a number of atomic states close to the ionisation limit (‘Rydberg’ states) a wavepacket is created which behaves more or less as a classical electron – the wavepacket is concentrated in space and distance to nucleus varies periodically with time. The probability that such a state will absorb photons varies periodically with time also and is a maximum when the wavepacket is close to the nucleus. When the ‘wavepacket’ is far from the nucleus it behaves essentially as a ‘free’ electron and a free electron cannot absorb photons because momentum cannot be conserved. If the pulse that excites the Rydberg states is so short that it turns off before the wavepacket returns from being close to the nucleus, then there is no time to absorb more photons while the atom is in the excited state and the resonance, which would occur in a long pulse, is suppressed.
Secondly, other experiments, carried out under rather different conditions, tend to show that the ionisation rate is much lower than predicted. The reason for this is not yet understood. For short pulses (less than 10 fs), the laser bandwidth becomes so large that many atomic states are resonant. Strangely enough, numerical simulations show that the ionisation rate is then decreased as if the electron remained trapped in the discrete spectrum.
New regions of research are opening up with the new tabletop ultra-powerful lasers. Intensities between 1019 and 1021 W cm–2 are likely to be achieved within the next year or so. A totally new class of processes is expected, ranging from the complete stripping of all electrons from atoms to vacuum polarisation phenomena: the generation of light at a frequency three times that of the light used – a very common process in dense media which at sufficient intensities becomes possible in a vacuum. The results summarised here may have been obtained at a more modest intensity, but they contain enough surprises to make one think that many more are waiting for us in the very near future.
Further reading
P Agostini and G Petite 1988 Photoelectric effect under strong irradiation Contemp. Phys. 29 57
May 1987 Special issue of J. Opt. Soc. America B 4 765
1988 The ponderomotive potential of high intensity light and its role in multiphoton ionization of atoms IEEE J. Quantum Electron. 24 1461